重力波與相對論: 關於重力波的理論歷史發展
- 物理專文
- 撰文者:倪維斗 (清華大學物理系)
- 發文日期:2017-12-20
- 點閱次數:1970
2015 年 9 月 14 日,LIGO (LIGO: Laser Interferometer Gravitational-Wave Observatory; 美國在華盛頓州 Hanford 和路易斯安那州 Livingston 建造的兩 個 4 公里臂長雷射干涉重力波探測天文台) 團隊和 Virgo (義大利和法國在 Pisa 地區建造的 3 公里臂長重力波探測天文台) 團隊以 LIGO 兩個相距 3000 公里、 臂長 4 公里的重力波干涉儀探測到了距離我們約 13 億光年的兩個約 為 30 太陽質量黑洞的互繞及合生所產生的重力波。信號持續時間為 0.2 秒。 合生時最大的重力波亮度大於可觀測到的宇宙所有恒星亮度的總合。達到 探測器時最大的重力波應變為 10−21,對 4 公里臂長的長度變化為 4 am (attometer; atto 為 10−18 之義),約為鋁原子核的千分之一。LIGO 團隊和 Virgo 團隊在 2 年內已宣佈發現了 6 對黑洞的合生重力波。 並在 2017 年 8 月 17 日探測到了距離我們約 1.3 億光年的雙中子星互繞及合生所產生的重 力波,奠定了多信使天文學的基石,驗證了光速和重力波速相同到 3 x 10−15 之程度。重力波的探測開啟了天文學新的領域,進一步的發展可使靈敏的 干涉儀探測大部分可觀測的宇宙,無需以管窺天,可以說是人類科學發展 上的極至。 而這極至的達成有賴理論的建立和 60 年來實驗的發展。
波動
波動簡單的分類有三種:標量波、向量波與張量波。
聲波: 密度標量波,可以有單極輻射;其波動方向和傳播方向相同,因之是縱波。
電磁波: 向量波,沒有單極輻射,可以有二極輻射;其波動方向和傳播方向垂直,是橫波。
地震波: 應變張量波;其波動方向,一般有垂直於傳播方向的部分和平行於傳播方向的部分。
重力波: 是時空變化的張量波,沒有單極和二極輻射,可以有四極輻射;其波動方向和傳播方向垂直,和電磁波一樣,也是橫波。
廣義相對論
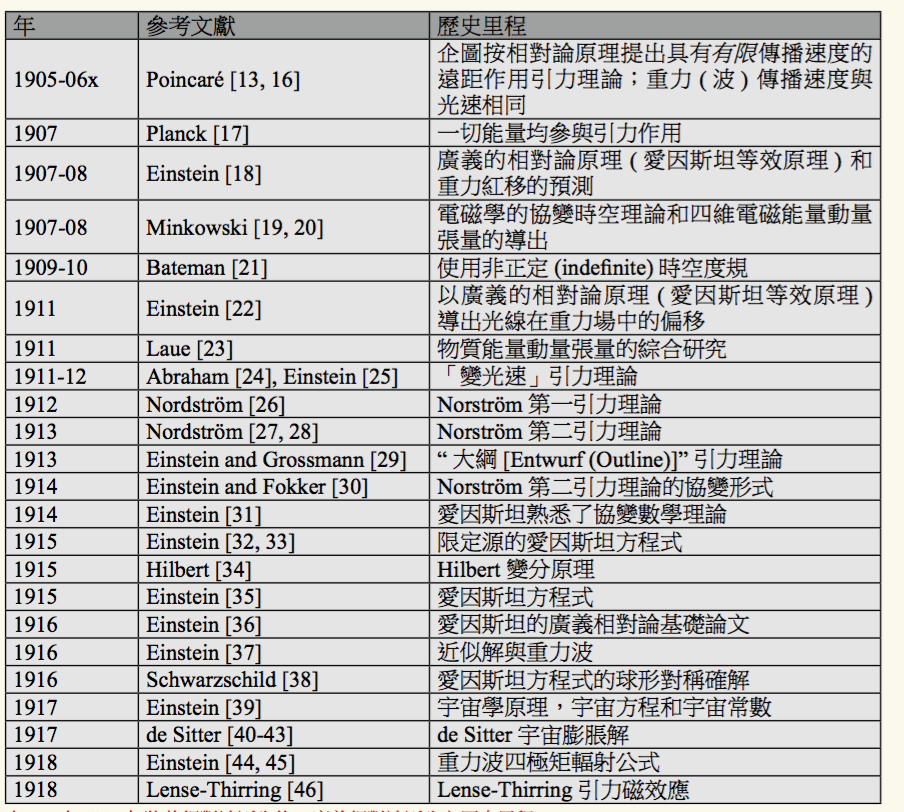
說起重力波,我們必須簡述一下廣義相對論的發展史。1859年,法國天文學家Le Verrier發現水星近日點的前進超出牛頓萬有引力計算行星擾動所預測的結果,進動的差異每百年有38角秒的幅度。這個異常打破了牛頓引力理論。這個發現最終引導出來了廣義相對論。1887年,美德物理學家 Michelson 和美國化學家 Morley 實驗發現光速不因地球運動的方向而變,打破了牛頓動力學的基礎,引出了狹義相對論。表1列出在1905年狹義相對論誕生前,促使新引力理論發展之重要歷史里程。表2列出在1905年狹義相對論誕生後,廣義相對論誕生之歷史里程。
表一:在1905年狹義相對論誕生前,促使新引力理論發展之重要歷史里程。
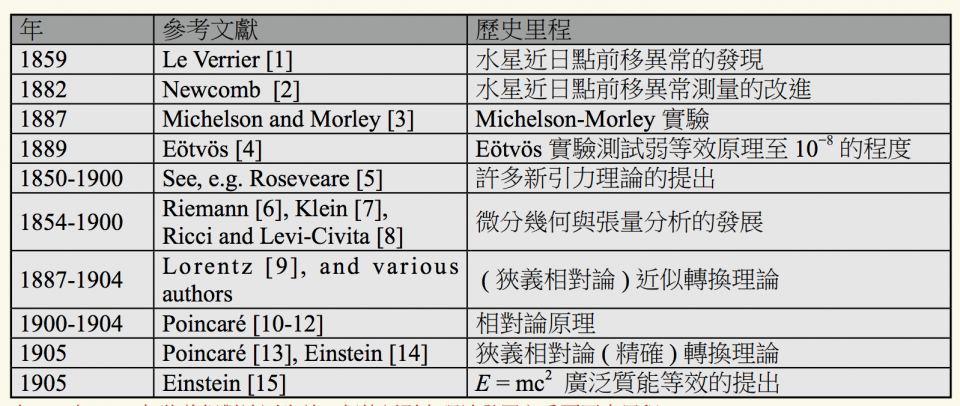
1887-1904年,羅倫茲和許多作者提出了各種狹義相對論二階協變轉換理論。1904年,羅倫茲所提已滿足了所有當時的實驗與觀測。發展的同時,潘加瑞 (Poincaré) 在1990-1904年提出相對論原理 [The laws of physical phenomena must be the same for a fixed observer and for an observer in rectilinear and uniform motion so that we have no possibility of perceiving whether or not we are dragged in such a motion. (對於一個固定的觀察者和一個直線勻速運動的觀察者來說,其物理現象的定律,必須是相同的,我們不可能察覺在此運動中是否被拖曳的。)],並在1905年提出了精確的狹義相對論協變轉換理論,並稱此不同慣性坐標系間的轉換為羅倫茲轉換;隨後愛因斯坦也提出了相同的狹義相對論協變轉換理論,繼而提出質能相當公式 E = mc2的普遍性。
1905-1906年,潘加瑞嘗試提出與狹義相對論相容的遠距作用引力理論,並提出重力的傳播速度與光的相同。1907年,普朗克提出所有能量必須參與引力相互作用 (因質能等效)。1907-1908年,愛因斯坦提出廣義相對論原理,即現稱的愛因斯坦等效原理,並由此推導出重力紅位移。愛因斯坦認為提出此原理是他此生最快樂的事。愛因斯坦等效原理奠定了相對論性引力理論發展的基礎。1911年,愛因斯坦使用其等效原理,推導出光線在重力場中的偏折 (其值為廣義相對論的一半)。
1907-1908年,Minkowski 提出 Maxwell-Lorentz 電磁學的四維時空協變理論,並推導出四維電磁場能量動量張量。
1911年,Laue 綜合提出了物質的能量動量。
1911-1913年,Abraham、愛因斯坦、Norström 分別提出了各種標量場引力理論。
1913年,愛因斯坦和 Grossmann 提出了稱為「大綱」的引力理論。
1915年 (11月4日報告、11月11日出版;11月11日報告、11月18日出版),愛因斯坦提出了限制引力源的愛因斯坦方程式。1915年 (11月18日報告、11月25日出版),愛因斯坦按其新的理論改正了1913年和 Besso 合作計算的水星近日點進動中的錯誤,得到和觀測相吻合的結果。
1915年 (11月20日報告),Hilbert 得到正確的引力變分原理 (Hilbert Variational Principle),可以推導出不限制引力源的愛因斯坦方程式。
1915年 (11月25日報告、12月2日出版),愛因斯坦提出了不限制引力源的愛因斯坦方程式,完成了廣義相對論理論。
1916年,愛因斯坦提出了綜合性的廣義相對論基礎論文,同年,愛因斯坦提出了廣義相對論線性近似解與重力波。
1915年,Schwarzschild從愛因斯坦11月25日出版的水星近日點論文的近似解開始,發現了球形對稱確解。愛因斯坦水星近日點論文的近似解是使用其在11月18日出版的限制引力源的愛因斯坦方程式,此方程式對於真空而言,和廣義相對論的真空方程式相同,故Schwarzschild 球形對稱確解也是廣義相對論的解。論文於1916年1月13日提交;1916年2月,Schwarzschild 再提交了帶球形對稱內部物質的 Schwarzschild 解。Schwarzschild於1916年5月11日去世。
1913年開始,Droste在萊登大學羅倫茲教授的指導下從事廣義相對論的研究工作。1916年5月27日,Droste 提交了一篇論文,非常清楚且易懂的推導出球形對稱解,並廣泛地分析了測試質點在此球形對稱解中的運動。此解的度規與Schwarzschild 坐標下的Schwarzschild 度規相同。
Schwarzschild 坐標下的Schwarzschild 度規在 R = 2 GNM/c2 (GN為牛頓引力常數;c 為光速) 處為奇異的。在1922年,Lanczos明確的指出度規分量的奇異性並不必然具有物理意義。直到38年後 Kruskal 和 Szekeres 才分別發現 Schwarzschild 確解的極大延伸和完全規則的坐標表示。
1916年3月 Reissner 發表了一篇有關Schwarzschild 解推廣到帶有電荷的重力源之論文;Weyl在1917年,Nordström 在1918年完成了此推廣解的工作;此帶電荷的解稱為Reissner-Nordström解。至於軸對稱的確解,雖然有許多的嘗試,直到1963年,才為Kerr發現,帶有角動量,稱為 Kerr 解。1965年,Newman 和 Janis 推廣 Kerr 解, 發現軸對稱並帶有角動量和電荷的確解,稱為 Kerr-Newman 解。Kerr-Newman解若不帶角動量,則成為Reissner-Nordström解。
1960年代,開始廣泛地研究奇異結構 (奇點等;Singularities) 和視界 (Horizon),瞭解 Schwarzschild 解和Kerr-Newman 解均有視界,均為黑洞。在廣義相對論中,這些解是僅有的真空解。物質進了黑洞,則在古典物理的範疇中不能復出。在天體物理中,若黑洞帶有電荷,則容易吸引周遭的反電荷,不容易累積,因之,帶的電荷極少,接近 Kerr 黑洞。
愛因斯坦等效原理假設局部物理為狹義相對論物理 (Local physics is special relativistic physics.):宇宙中任何時刻、任何地點在其局部慣性系下的物理方程式,均和羅倫茲慣性坐標下的物理方程式相同。此原理應用於計量學與 (非人造) 計量標準上,即為假設其普適性。計量學普適性的成立同時也驗證了愛因斯坦等效原則。
讀者也許心中有個問題,如果如此,那麼什麼是引力 (重力) 呢? (What is GRAVITATION?) 答案是,重力理論告訴我們這些局部物理是怎麼相接成大域物理的;重力加速度可以用等效原理化為等效的慣性力,真正的重力是一種潮汐力、或稱為引潮力 (如:在地球上若無引潮力,我們即難以觀察太陽和月亮的引力)。就好像二維局部歐式空間的不同連接可以構成球面或其它曲面;四維局部閔氏 (羅倫茲) 時空的不同連接可成為帶有重力的各種彎曲時空。
廣義相對論是一萬有引力理論。在牛頓引力理論中,兩個物體所產生的引力是可以線性疊加的。在愛因斯坦廣義相對論中,兩個物體所產生的引力必須以非線性疊加,而且是增強的。一個結果是可以有黑洞解,即黑洞裡的粒子無法跑出其視界 (Horizon)。黑洞可以說是引力場中最簡單的解,僅有質量、角動量和電荷三種特性。在自然界,這些解所帶有的電荷會吸引周遭的反電荷,絕大部分會被中和,因此,帶電量極低,基本上可用質量和角動量描述。因之,宇宙於天體環境中的黑洞基本上可以用Kerr 黑洞來描述,帶有質量和角動量 (自旋) 兩種特性。
狹義相對論時空可用閔氏度規描述,廣義相對論時空是由局部閔氏度規連結而成,可用時空度規張量描述。時空的波動稱為重力波,可用時空度規張量的週期變化或頻譜描述。當重力波傳入探測器時,時空的週期變化引起探測器的反應,在共振探測器引起探測器應變的共振而探知,在雷射干涉儀引起兩反射鏡間距離之變化而探知。
繼續閱讀:重力波與相對論: 開啟重力波觀測,力波與相對論: 探測重力波的世代
1. U. J. J. Le Verrier, Theorie du mouvement de Mercure, Ann. Observ. imp. Paris (Mém.) 5, 1- 196 (1859).
2. S. Newcomb, Discussion and results of observations on transits of Mercury from 1677 to 1881, Astr. Pap. am. Ephem. naut. Alm., 1, 367-487 (U.S. Govt. Printing Office,
Washington, D.C., 1882).
3. A. A. Michelson and E. W. Morley, On the relative motion of the Earth and the luminiferous ether, Am. J. Sci. 34, 333-345 (1887).
4. R. V. Eötvös, Ü ber die Anziehung der Erde auf verschiedene Substanzen, Math. Naturwiss. Ber. Ungarn 8, 65 (1889).
5. N. T. Roseveare, Mercury's Perihelion from Le Verrier to Einstein (Oxford, Clarendon Press, 1982); the reader is referred to this book for a thorough study of the history
related to the Mercury's perihelion advance.
6. B. Riemann, Ü ber die Hypothesen welche der Geometrie zu Grunde liegen (On the hypotheses which underlie geometry), lecture at Göttingen (1854).
7. F. Klein, Programm zum Eintritt in die philosophische Fakultät d. Univ. zu Erlangen, Erlangen, A. Deichert, 1872. Reprinted in 1893 in Math. Ann. 63, and in Klein’s Ges. Math.
Abhandl. I, 460.
8. G. Ricci and T. Levi-Civita, Méthodes de calcul différentiel absolu et leurs applications, Mathematische Annalen (Springer) 54 125-201 (1900).
9. H. A. Lorentz, Kon. Neder. Akad. Wet. Amsterdam. Versl. Gewone Vergad. Wisen Natuurkd. Afd. 6, 809 (1904), and references therein.
10. H. Poincaré, Bibliothéque du Congrés International de Philosophie 3, 457 (1900).
11. H. Poincaré, La Science et l’Hypothése (Flammarion, Paris, 1902); English translation in Science and Method (London: Dover Publications Inc. 1952).
12. H. Poincaré, L’état et l’avenir de la physique mathematique, Bulletin des Sciences Mathématiques 28, 302-324 (1904); the English translation is from C. Marchal, Sciences
97-2 (April, 1997) and English translation provided by the author.
13. H. Poincaré, Sur la dynamique de l’electron, C. R. Acad. Sci. 140, 1504 (1905).
14. A. Einstein, Zur elektrodynamik bewegter Körper [On the Electrodynamics of Moving Bodies], Ann. Phys. (Germany) 17, 891-921 (1905).
15. A. Einstein, "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?", Ann. Phys. 18, 639-641 (1905).
16. H. Poincaré, Sur la dynamique de l’electron, Rendiconti del Circolo Matematico di Palermo 21, 129 (1906).
17. M. Planck, Zur Dynamik bewegter Systeme, Sitzungsberichte der Königlich-Preussischen Akademie der Wissenschaften, Berlin, 13, June 1907, 542-570 (Specially at p. 544);
(English translation) On the Dynamics of Moving Systems (1907), by Max Planck, translated from German by Wikisource,
https://en.wikisource.org/wiki/Translation:On_the_Dynamics_of_Moving_Systems.
18. A. Einstein, Ü ber das Relativitätprinzip und die aus demselben gezogenen Folgerungen, Jahrb. Radioakt. Elektronik 4, 411-462 (4 December, 1907); Corrections by Einstein in
Jahrb. Radioakt. Elektronik 5, 98 (1908); English translations by H. M. Schwartz in Am. J. Phys. 45, 512, 811, 899 (1977).
19. H. Minkowski, Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern, Königliche Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-
Physikalische Klasse. Nachrichten, pp. 53-111 (1908); this paper was read before the Academy on 21 December 1907; (English translation) The fundamental equations for
electromagnetic processes in Moving bodies, translated from German by Meghnad Saha and Wikisource,
http://en.wikisource.org/wiki/Translation:The_Fundamental_Equations_for_Electro...
20. H. Minkowski, Raum und Zeit, Physik. Zeitschr. 10 (1909) 104–111. For an English translation see the book The Principle of Relativity by H. A. Lorentz, A. Einstein, H.
Minkowski and H. Weyl, transl. by W. Perrett and G. B. Jeffery (Dover: New York, 1952).
21. H. Bateman, The transformation of the electrodynamical equations, Proc. Camb. Math. Soc., Ser. 2, 8, 223 (1910); received March 7, 1909, read March 11, 1909, revised July
22, 1909.
22. A. Einstein, "Ü ber den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes", Ann. Phys. 35, 898-908 (21 June 1911); translated "On the Influence of Gravitation on the
Propagation of Light" in The collected papers of Albert Einstein. Vol. 3: The Swiss years: writings, 1909–1911 (Princeton University Press, Princeton, New Jersey, 1994), Anna
Beck translator.
23. M. von Laue, Zur Dynamik der Relativitätstheorie, Annalen der Physik 35, 524-542 (1911); M. von Laue, Das Relativitätsprinzip (Friedrich Vieweg und Sohn, 1911)..
24. M. Abraham, Lincei Atti 20, 678 (Dec. 1911).
25. A. Einstein, Ann. Phys. 38, 355, 443 (Feb. 1912).
26. G. Nordström, Phys. Zeit. 13, 1126 (2012).
27. G. Nordström, Ann. Phys. 42, 533 (2013).
28. G. Nordström, Ann. Phys. 43, 1101 (2014).
29. A. Einstein and M. Grossmann, Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation [Outline of a Generalized Theory of Relativity and of a
Theory of Gravitation], Zeitschrift für Mathematik und Physik 62, 225–261 (1913).
30. A. Einstein and A. D. Fokker, Ann. Phys. 44, 321 (1914).
31. A. Einstein, “Die formale Grundlage der allgemeinen Relativitätstheorie,” (submitted on October 29, 1914) Königlich Preußische Akademie der Wissenschaften (Berlin).
Sitzungsberichte, 1030–1085 (1914); English translation in The Collected Papers of Albert Einstein, Volume 6: The Berlin Years: Writings, 1914-1917 Albert Einstein (English
translation supplement) Page 30-84, Edited by Martin J. Klein, A. J. Kox, Jürgen Renn, and Robert Schulmann (Princeton University Press1995); available on line,
http://press.princeton.edu/einstein/digital/.
32. A. Einstein, Zür allgemeinen Relativitätstheorie, Preuss. Akad. Wiss. Berlin, Sitzber. 778-786 (1915); English translation in The Collected Papers of Albert Einstein, Volume 6:
The Berlin Years: Writings, 1914-1917 Albert Einstein (English translation supplement) Page 98-107, Edited by Martin J. Klein, A. J. Kox, Jürgen Renn, and Robert Schulmann
(Princeton University Press1995); available on line, http://press.princeton.edu/einstein/digital/..
33. A. Einstein, Zür allgemeinen Relativitätstheorie (Nachtrag), Preuss. Akad. Wiss. Berlin, Sitzber., 799-801 (1915); English translation in The Collected Papers of Albert Einstein,
Volume 6: The Berlin Years: Writings, 1914-1917 Albert Einstein (English translation supplement) Page 108- 110, Edited by Martin J. Klein, A. J. Kox, Jürgen Renn, and Robert
Schulmann (Princeton University Press 1995); available on line, http://press.princeton.edu/einstein/digital/..
34. D. Hilbert, Die Grundlagen der Physik, Konigl. Gesell. d. Wiss. Göttingen, Nachr., Math.-Phys. KL., 395-407 (1915).
35. A. Einstein, Die Feldgleichungen der Gravitation, Preuss. Akad. Wiss. Berlin, Sitzber., 844-847 (1915); English translation in The Collected Papers of Albert Einstein, Volume
6: The Berlin Years: Writings, 1914-1917 Albert Einstein (English translation supplement) Page 117-120, Edited by Martin J. Klein, A. J. Kox, Jürgen Renn, and Robert
Schulmann (Princeton University Press, 1995); available on line, http://press.princeton.edu/einstein/digital/..
36. A. Einstein, Die Grundlage der allgemeinen Relätivitatstheorie, Ann. Phys. 49, 769 (1916).
37. A. Einstein, Näherungsweise Intergation der Feldgleichungen der Gravitation, Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin, June 22, 1916) pp.
688-696; English translation (translated by Alfred Engel) in The Collected Papers of Albert Einstein, Volume 6: The Berlin Years: Writings, 1914-1917 (English translation
supplement, Doc. 32, pp. 201-210, Princeton University Press, http://einsteinpapers.press.princeton.edu/vol6-trans).
38.K. Schwarzschild, "Ü ber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie", Sitzungsberichte der Königlich Preussischen Akademie der
Wissenschaften 7, 189– 196 (1916); English Translation, S. Antoci and A. Loinger, "On the gravitational field of a mass point according to Einstein's theory",
arXiv:physics/9905030.
39. A. Einstein, Kosmologische Betrachtungen zur allgemeinen Relativitaetstheorie, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin. part 1,
142–152 (1917).
40. de Sitter, W. "On the Relativity of Inertia: Remarks Concerning Einstein's Latest Hypothesis." Proc. Kon. Ned. Akad. Wet. 19, 1217-1225 (1917).
41. de Sitter, W. "The the Curvature of Space." Proc. Kon. Ned. Akad. Wet. 20, 229-243 (1917).
42. de Sitter, W. Proc. Kon. Ned. Akad. Wet. 20, 1309 (1917).
43. de Sitter, W. Mon. Not. Roy. Astron. Soc. 78, 3 (1917).
44. A. Einstein, Ü ber Gravitationswellen, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften (Berlin, February 21, 1918) pp. 154-167; English translation
(translated by Alfred Engel) in The Collected Papers of Albert Einstein, Volume 7: The Berlin Years: Writings, 1918-1921 (English translation supplement, Doc. 1 “On
gravitational waves”, pp.9-27, Princeton University Press, http://einsteinpapers.press.princeton.edu/vol7-trans).
45. A. S. Eddington, The propagation of gravitational waves, Proc. Roy. Soc. London A 102, 268– 282 (1922).
46. Lense and H. Thirring, Phys. Zeits. 19, 156 (1918); English translation in Gen. Rel. Grav. 16, 712 (1984).
參考文獻
1. 倪維斗,無遠弗屆、鉅細靡遺 -- 全方位的重力波探測,科學月刊,2017年12月,第934-941頁。
2. Wei-Tou Ni, Genesis of general relativity – A concise exposition, Int. J. Mod. Phys. D, 25, 1630004 (2016).
3. Chiang-Mei Chen, James M. Nester and Wei-Tou Ni, A brief history of gravitational wave research, Chinese Journal of Physics 55, 142-169 (2017).
4. Kazuaki Kuroda, Wei-Tou Ni and Wei-Ping Pan, Gravitational waves: Classification, Methods of detection, Sensitivities, and Sources, Int. J. Mod. Phys. D, 24, 135031 (2015).
5. Wei-Tou Ni, Gravitational Wave (GW) Classification, Space GW Detection Sensitivities and AMIGO (Astrodynamical Middle-frequency Interferometric GW Observatory), arXiv: 1709.05659.
6. LIGO Scientific Collaboration and Virgo Collaboration, Femi GMB ed. al., Multi-messenger Observations of a Binary Neutron Star Merger, Astrophys. J. Lett., 848, L12 (59 pp) (2017).
7. LIGO Scientific Collaboration and Virgo Collaboration, Fermi Gamma-ray Burst Monitor, and INTEGRAL, Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A, Astrophys. J. Lett., 848, L13 (27 pp) (2017).
8. A. Sesana, Prospects for multiband gravitational-wave astronomy after GW150914, Phys. Rev. Lett. 116, 231102 (2016).
9. W.-T. Ni, G. Wang and A.-M. Wu, Astrodynamical Middle-frequency Interferometric GW Observatory AMIGO: mission concept and orbit design, paper in preparation.
10. Wei-Tou Ni, Gravitational wave detection in space, Int. J. Mod. Phys. D, 25, 1630001 (2016).