如何看懂物理公式 (三) ：以數學運算取代邏輯推理

在這一系列的專欄中，我們已分別討論過「定義」與「定律」的特性，其中無論是想清楚地描述某個觀念的意義，或是要明確地表達透過實驗歸納而得出的結果，由於內容涉及變數之間的數量關係，因此數學方程式往往是最佳的表達方式。所以，除了理解物理公式之中，各個物理量之間的正比或反比關係之外，能根據已知的物理公式來做推理與演繹，也是「看懂物理公式」的一個重要能力。

對許多同學而言，等加速度運動公式可說是在高中物理課程遭遇到的第一道難題，能否掌握這些公式，可算是踏入物理學世界的第一道門檻。本文將透過這四個公式，向初學物理的同學展示，物理學家如何透過數學運算來取代邏輯推理，如何從定義出發，演繹出重要或有趣、有用的推論，讓同學看到「學物理」的另一個面貌，並理解「學物理」與「學數學」是可以相輔相成的兩件事。


運動學：以數學為語言來描述運動的方法

描述物體運動的方式是透過位置座標 (x) 、位移 (∆x) 、時間 (t) 、速度 (v) 與加速度 (a) 這幾個變量來完成的，雖然直觀上來說，這不是很困難，但當大多數同學第一次在物理課堂上，接觸到這個主題時，相信很多人都因為它而卻步了，因為眼前的這些數學方程式，讓明明不是很困難的觀念，變得複雜與抽象！ (如果你稍後有了想翻頁跳過本文的念頭，或許就是最好的證明了！) 

當物體在運動時，最明顯的就是它的位置會發生改變，精確來說是「隨時間而變」。因此，描述物體運動的快慢程度，也就是速度的定義，是以位置的變化量 (∆x，末位置減去初位置，稱為位移) 除以時間間隔 (∆t) ：

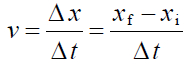
根據這個定義，可以得出二個簡單的推論，當物體做｢等速度」運動時：
•    位移的大小等於速度乘以時間 (∆x = v ∙ ∆t)；
•    運動所需的時間等於位移除以速度 (∆t = ∆x/v) 。

附帶一提，在日常生活中，我們並沒有去區分「位移」與「距離」，或是「速度」與「速率」這些用語之間的差異，所以常常會聽到「速度等於距離除以時間」或是「距離等於速度乘以時間」等說法。然而，對於開始接觸高中物理的同學，要細分這些名詞的差別，以及它們的正負數值在「向量」上有著代表方向的意義，例如左右方，或東西方。

然而，當物體運動的速度「愈來愈快」或「愈來愈慢」時，位移就不再只是速度乘以時間這麼簡單而直接了。

早在四百多年前，伽利略以數學式的方式，寫下我們如今熟悉的「加速度」的定義：

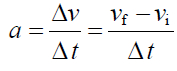
雖然它與速度的定義，在數學上的模式相同，但卻能讓我們對於「愈來愈快」或「愈來愈慢」的運動情形，有了明確而清楚的認知，所以其實是一件很了不起的事情。

當物體的速度發生變化時，我們便說這個物體有加速度，雖然在日常生活中，我們會有「減速度」的說法，但在物理課堂上，比較正式的說法是「負的加速度」或「加速度為負值」。我們之所以偏好這個說法，是因為透過正負值，我們可以把加速度進一步抽象為數學裡的「向量」，亦即具有大小與方向性的物理量，例如剛剛所提到的位移與速度。


這樣定義會得出什麼結果？

讀者或許還記得我們曾經建議「看到定義時不要先問為什麼」，然而這並不表示「定義是沒有為什麼的」。相反的，物理學家之所以會下某個定義，往往是因為有了這個定義之後，可以得出一些有意義的結果。

以加速度的定義為例，在正式學習微積分之前，雖然「忽快忽慢」的問題還是無法處理，但是對於「穩定地」加速或減速的運動，也就是「等加速度運動」的情形，我們倒是可以透過代數運算，推理出一些很有意思的結果。

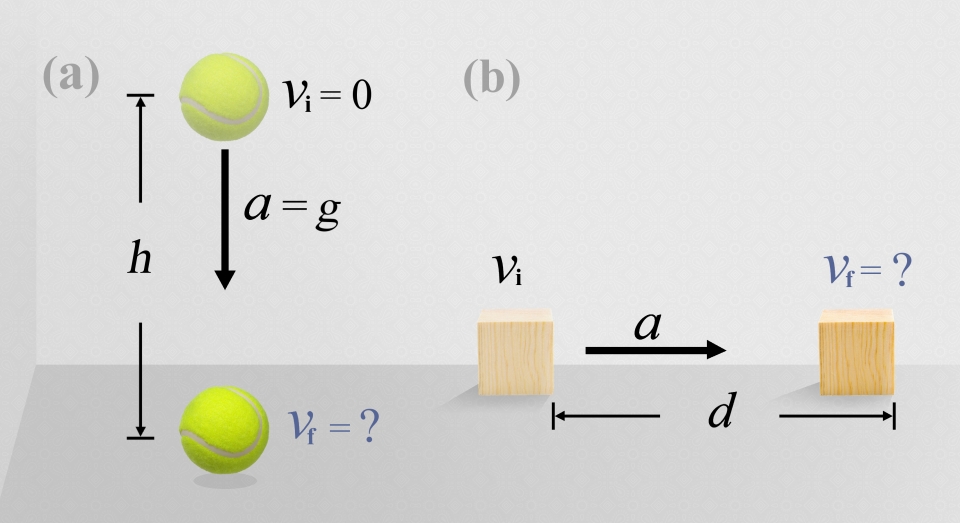
首先是末速度的公式。如圖一 (a) 所示，假設在啟動碼錶的瞬間，我們知道物體的初速度 (v_i) 與加速度 (a) ，那麼在一段時間 (t) 之後，物體的末速度 (v_f) 速度為 (圖一) ：
 

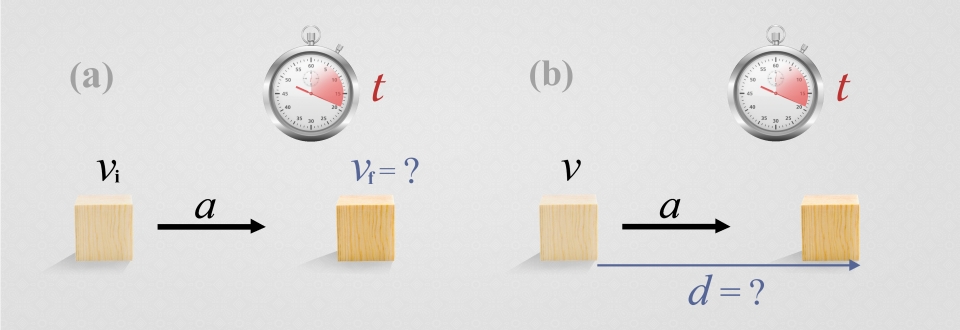
圖一：已知初速度、加速度與運動時間，試問 (a) 末速度與 (b) 運動距離分別為若干？

這個看似複雜的數學公式，或許也曾讓許多許多學生對物理望之卻步，然而，只要能理解代數裡的移項運算 (或等量公理) ，就能理解這只是加速度定義的另一個版本：
       
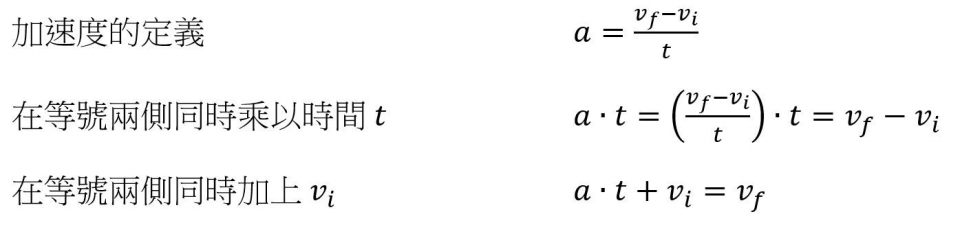
在習慣上，我們通常把代求的未知數寫在等號左側，因此左右對調一下即為公式1。


函數圖形面積的物理意義

接著我們再來看看位移的問題。如圖一 (b) 所示，假設已知條件與前問題相同 (已知初速度與加速度)，那麼在運動一段時間 (t) 之後，物體移動了多少距離？

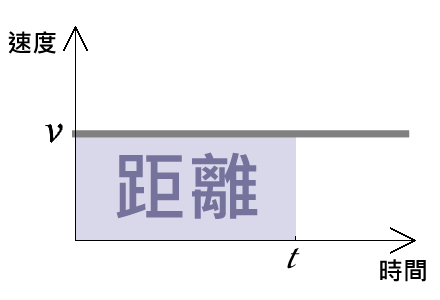
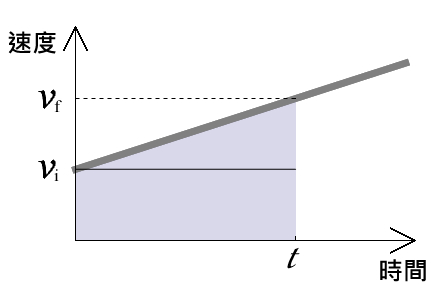
要解決這個問題之前，要先往回一步，從「等速度運動」與「距離」之間的關係開始思考。就等速度運動而言，運動的距離等於速度乘以時間，這個想法一點都不困難，但在這裡，我們得用一個「新的眼光」來看待這個想法：函數圖形。如果以速度為縱軸、時間為橫軸的速度－時間關係圖 (v-t 圖) 來看，等速度運動的 v-t 圖為一條水平的直線，如圖二所示。在這個關係圖中，「速度乘以時間」就是直線下方的長方形面積，因此，如果我們從 v-t圖來看，這個關係圖中的「面積」，就物理意義而言，就是物體運動所走的「距離」。

有了這一層理解之後，我們來看看物體從靜止 (初速度 v_i = 0) 開始加速到速度為 v (此即末速度v_f ) 的情形，從 v-t圖來看是一條通過圓點的傾斜直線，與坐標軸之間圍成一個三角形 (圖三) ，其面積大小為：  

 

 

    
                         
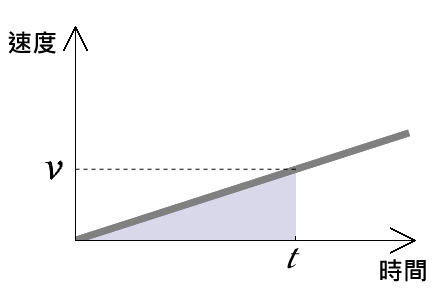
細心的同學應該發現了，在過程中，我們運用了先前求末速度的結果 (v_f = v = at) ，所得出來的這個「二分之一乘以加速度，再乘以時間平方」的結果，除了是v-t 圖中的三角形面積大小之外，更是等加速度運動的距離。

萬一物體不是從靜止開始加速，而是一開始便具有初速度 v_i 呢？從 v-t 圖來看，現在是一條不通過圓點的傾斜直線，如圖四所示。它與坐標軸之間會圍出一個「梯形面積」，其大小為

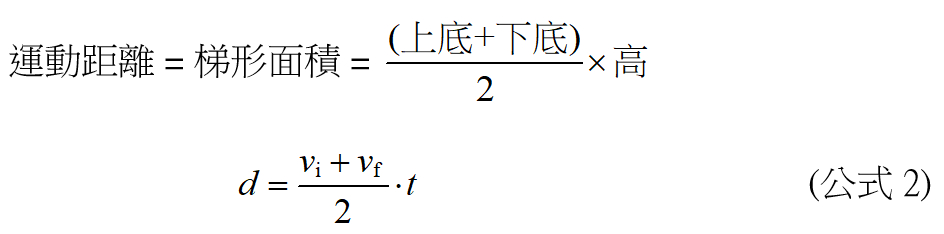
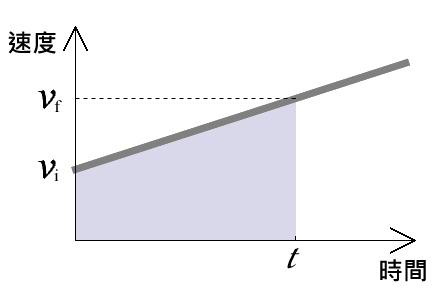
然而，如果我們在 v_i 的位置處劃一條水平的輔助線 (圖五) ，那麼這個梯形面積就可看成是「長方形加上三角形」。結合先前等速度與等加速度這兩個推論的結果，物體運動的距離可以寫成：

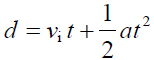                (公式3)

截至目前為止，在定義了速度與加速度之後，我們只透過代學裡的移項運算以及面積計算，便得出了三個重要的運動學公式，用以描述物體在等加速度運動下的情況。


萬一我們不知道運動的時間呢？

現在，我們來看一個簡單的生活實例，假設我們拿一個網球，如圖六 (a) 所示，讓它從胸口的高度往下掉落 (掉落高度約1.5公尺)，網球在著地前瞬間的速度是多少？

在回答這個問題之前，我們應該知道，地球表面附近的運動可視為等加速度運動 (a = g = 9.8 ms^-2) ，在這麼短的距離內，空氣阻力的影響可以忽略不計。

然而，以我們目前的理解，我們無法單獨透過某一條公式來求得末速度，因為網球在著地前的運動時間也是一個未知數。

我們也可以從水平的方向，重新看待這個問題，如圖六 (b) 所示：物體由靜止開始做等加速度運動，已知其運動距離 d，但不知運動所經歷的時間，試問物體的末速度？
 

數學運算可以取代複雜的邏輯推理

這個問題的關鍵在於，我們已知初速 v_i、加速度 a 與運動距離 d，未知數是末速度 v_f，但因為少了時間 t 這個條件，所以，無法單獨靠一條公式就解決問題。

從數學的角度來看，由於有兩個未知數，所以需要兩條方程式才能求解。我們可以透過公式 3先求出時間，再利用公式1來求出末速。

或者，我們也可以利用「代入消去法」來求解公式1與公式3的聯立方程組。在此，由於我們缺少「時間」這個條件，所以，我們以數學的方法來消去它：

    以公式 1求得時間 (移項) ：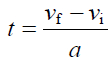       
 
    把時間代入公式 3：                   \(d=\nu _{i}\left(\frac{\nu _{f}-\nu _{i}}{a}\right)+\frac{1}{2}a\left(\frac{\nu _{f}-\nu _{i}}{a}\right)^{2}\)

    展開可得：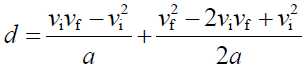                                

    計算 (通分、化簡) 可得：      \(d=\frac{2\nu _{i}\cdot\nu _{f}-2\nu _{i}^{2}}{2a}+\frac{\nu _{f}^{2}-2\nu _{i}\bullet\nu _{f}+\nu _{i}^{2}}{2a}=\frac{\nu _{f}^{2}-\nu _{i}^{2}}{2a}\)

    移項整理可得：                         v_f² = v_i² + 2ad     (公式 4) 

雖然我們費了一番功夫才得出公式 4，但是整個計算過程都符合嚴謹的邏輯推理，因此，在等加速度運動的條件下，公式4讓我們可以在「不知道時間」的情況下，單單憑藉著初速、加速度與運動距離，就可以得出末速度。以我們剛剛的網球問題為例，從胸口掉落的網球 (v_i = 0) ，在著地前那一瞬間的速度為：

 

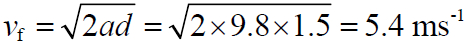
每秒5.4公尺的速度，時速將近20公里，其實還蠻快的。


是物理問題還是數學問題？

回到科學史的現場，有著深厚數學功底的伽利略，把實驗結果與數學模型完美地結合起來，從單擺的等時性，以及斜面實驗，不僅看出等速度運動與加速度運動的不同，更明確地以數學的語言來描述：等速度得運動距離與時間成正比，等加速度得運動距離與時間的平成成正比。從而提出慣性定律，並為日後的牛頓力學奠下基礎，而贏得「近代物理學之父」的美譽。簡單來說，如今，我們在運動學的課堂上，不過是重複伽利略所有過思維歷程而已。

至於牛頓，除了提出三大運動定律之外，更把「時間間隔」從 ∆t (一段時間) 縮小到趨近於零的 dt (一瞬間)，嚴謹地思考平均速度、平均加速度與瞬時速度、瞬時加速度之間的差異，寫下《自然哲學的數學原理》，有別於德國的哲學家、數學家萊布尼茲，從運動學的角度，獨立發展出微積分。這也是一個物理與數學之間，難分難解的公案。

在電路學中，類似的例子是克希何夫定則，根據電荷守恆 (結點定則) 與能量守恆 (迴路定則) 兩大原理，只需逐步列出聯立方程組，透過數學運算，就能省去電流、電壓等複雜的邏輯推理，而解決實際的電路問題。

電磁學中的馬克士威方程式，更是一個著名的例子。馬克士威於1864年發表《電磁場的動力學理論》，提出電場和磁場以波的形式以光速在空間中傳播，從而推論出光是電磁波的一種。稍後於1886年到1888年期間，德國物理學家赫茲在實驗室中驗證他的理論，從而開啟了無線電的時代。在馬克士威的百歲紀念誕辰上，愛因斯坦讚譽他對物理學做出了「繼牛頓時代以來，最深刻、最富成效的」成果，然而，這位把電、磁與光統一起來的偉大物理學家，當年在被訪問到自己是如何得出這些靈感時，他卻謙虛地表示：我只是把法拉第的工作「數學化」而已；而他口中的法拉第的工作，就是我們所熟知的電力線、磁力線的圖形 (如圖七)。
 

結語：送「禮物」別忘了要附上「卡片」

物理與數學，理論與實驗，孰重孰輕，孰先孰後，往往無法以一刀兩斷的方式來區分清楚。從學習物理的角度而言，動手做實驗的經驗與體驗，當然非常重要，然而透過數學式來表達物理觀念，以及相關推理的能力，也是不能偏廢的能力與素養。

學校的物理課程裡，曾經存在過許多艱深的數學問題，在考試領導教學的影響下，動手做實驗的機會逐漸被忽略，演變成只專注於反覆演練試題的填鴨式教學，這樣的教學模式當然叫人詬病。然而，從另一個角度來說，如果只強調「動手做實驗」而輕忽了「動腦思考實驗」，或是把物理觀念等同於「文字說明」，而對「物理公式」避之如蛇蠍，也是過猶不及的作法。

紐西蘭的物理試卷評分有三個等級，同學若要想拿到卓越 (E) 的滿級分，通常需要以文字，配合繪圖或相關的物理定義、定律、定理或原理等，針對問題情境中的物理觀念提出完整的解釋 (請參閱前文：沒有「一百分」的考試)。至於學生無法拿到滿分的原因，可能是只會計算，但文字的觀念解釋卻偏弱，或是「落落長」的寫了一大篇文字說明，卻少了一個可以「畫龍點睛」的方程式。因此，每當需要在課堂講解試題時，我的結語笑話都是：在送女朋友巧克力 (禮物) 時，還得附上卡片，才能完整表達心意！




延伸閱讀：
沒有「一百分」的考試
如何看懂物理公式 ( 一 ):定律篇
如何看懂物理公式 (二)：定義篇