
如何看懂物理公式 (二):定律篇
- Play-Create-Learn 紐西蘭科學與物理教育點滴
- 撰文者:蔡坤憲
- 發文日期:2019-08-13
- 點閱次數:8963
物理定律的英文原文是law,而這個字在日常生活中,有「法律」的意思。粗略來說,如同法律規範著人類社會的許多行為一樣,自然規律 (laws of nature) 或物理定律 (laws of physic) 則規範著大自然或物理世界中的許多行為與現象。而且,就像法律還可再細分成民法、刑法等,各有各自的適用範圍一樣,在力、熱、聲、光、電、高速或微觀等不同的物理世界中,也有其各自適用的物理定律。
在物理學中,凡能被稱作「定律」的內容,就表示它是實驗與觀測的結果。也就是說,物理定律所描述的是一個「自然現象」。因此,當我們看到一條定律時,不要直接就問為什麼,而是要先弄清楚,這條定律所描述的現象或事件為何 (what),然後再去了解這條物理定律背後的實驗為何?當初的科學家或物理學家是「如何」(how) 發現這個自然現象的?稍後再來思考可能造成這個現象或行為背後的理由為何,也就是「為什麼」(why) 的問題。
描述自然現象有「定性」與「定量」兩個層次,並不是所有的物理定律都有一條相伴的數學公式。但我們千萬不要誤以為,能寫成數學公式的定律才是比較「高級」的定律,例如慣性定律,回到科學史當時的瞬間,它可說是一個石破天驚的發現,如果伽利略沒有發現「慣性」的存在,牛頓又如何能導出第二運動定律,從而寫下 F=ma (或 F=∆p/∆t ) 這條著名的公式?
本文將從克卜勒行星運動定律開始,凸顯「定律是實驗或觀測的結果」,接著以慣性定律為例,來探討「定律是發明或發現的問題」?最後則以紐西蘭的一個實驗教學與評量單元來介紹「物理定律DIY」的一個方法。
定律是實驗或觀測的結果
四百多年前,德國天文學家克卜勒 (Johannes Kepler) 所提出的「行星運動定律」,確立了「日心說」的地位。繼承自丹麥天文學家第谷 (Tycho Brahe) 多年收集的天文觀測資料,經過仔細分析與整理,克卜勒在1609年時首次發表了第一與第二定律,之後又過了約十年的時間,於1618年時發表第三定律。雖然,克卜勒本人並沒有為這些「發現」排序或編號,也沒有特別把它們與他的其它發現明顯地獨立分隔出來,但經後人的梳理,我們現在熟悉的克卜勒行星運動定律為:
第一定律:所有的行星皆以橢圓形軌道繞太陽運行,太陽位於橢圓其中之一的焦點位置上;又稱「軌道定律」。
第二定律:太陽與行星的連線半徑,在相同的時間內,會掃過相同的面積;又稱為「等面積定律」。
第三定律:行星公轉週期的平方,與其橢圓軌道的半長軸的三次方成正比;又稱為「週期定律」。
讓我們暫且拋下「為什麼」這個問題,而先專注在「現象的描述」上,這幾條定律告訴了我們些什麼事情?顧名思義,這是克卜勒根據 (實驗) 觀察的數據,描述了行星「如何」繞著太陽運行的方式。
讓我們以也是行星之一的地球來理解這幾條定律。首先,根據「軌道定律」,地球會以「橢圓形」的公轉軌道繞日運行。由於橢圓有兩個焦點,而太陽位在其中之一的焦點上,因此,地球在公轉軌道上的位置,會有遠日點與近日點的差別。
此外,我們知道地球自轉軸傾斜了23.4度,是造成一年四季的主因。由於日照的強度,角度比距離重要,加上地球是以由西向東的方向公轉,因此,在遠日點附近,雖然地球距離太陽較遠,但由於陽光直射北半球的緣故,因此是北半球的夏季。所謂的夏至 (6月21日左右) 是地球位於遠日點上,而冬至 (12月21日左右) 則是在近日點上 。
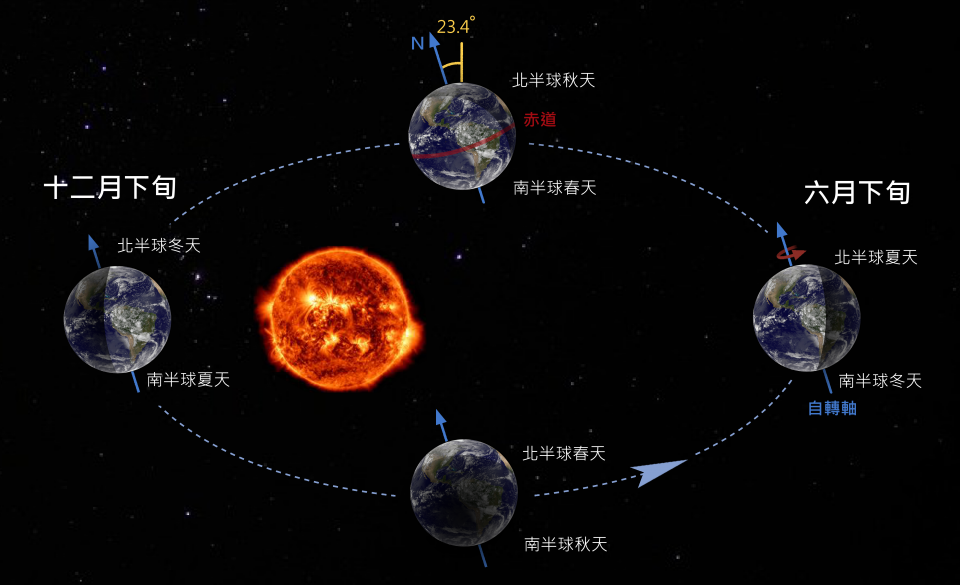
其次,「等面積定律」告訴我們:地球並非以等速率繞行太陽公轉,而是在距離太陽較遠時,公轉速率較慢;而距離太陽較近時,公轉速率則較快。
如果我們以春分與秋分為界 (如圖一所示) ,仔細計算一下地球從春分 (三月21日) ,經過夏季,公轉到達秋分 (九月23日) 的位置時,總共有186日的夏天。而從秋分開始,經過冬季再回到春分時,則只經過了179日,二者之間相差了七天左右 (這裡以一般的平年365天做估算,二月只有28天) 。到目前為止,我們完全沒有觸及「為什麼」的問題,單純根據克卜勒行星運動定律所描述的現象,便能與日常生活中「夏季比冬季長」的感覺相印證。
在我們仔細討論「週期定律」裡的數量關係之前,先來從「慣性定律」來看看定律的另一個特質。
定律是「發明」或「發現」的?
在十七世紀之前,人們普遍接受的亞里斯多德的主張,認為力是維持物體運動狀態 (速度) 的原因。然而,伽利略卻「發現」到:摩擦力是造成物體停止運動 (減速) 的原因。
伽利略通過科學實驗和邏輯推理,在他的著作《關於托勒密和哥白尼兩大世界體系的對話》 (1632年) 和《關於力學和運動兩門新科學的對話》 (1638年) 中,詳細地描述了一個實驗:

圖二 伽利略的慣性實驗:滾上右側軌道的小球速度會逐漸減緩,並有回復到相同高度傾向,隨著坡道傾斜程度逐漸減緩,小球所滾動的距離也隨之逐漸增長。 若右側為水平軌道,則球速不會減小,滾動距離也會「非常」遠。圖片編修自 THE MET (https://www.metmuseum.org)
這就是我們所熟悉的「慣性」實驗。然而,若放在日常生活裡,這個物體事實上根本無法「達到相同的高度」,也無法「永遠向前運動」,伽利略之所以能得出這樣的結論,是在他的心裡,透過移除了「摩擦力」這個因素,創造或「發明」出一個「完美」的世界,從而看到物體運動現象的一個「本質」:物體若不受外力作用,則靜者恆靜,而動者恆沿一直線作等速率運動。
因此,在學習的過程中,我們除了理解 (或熟記) 慣性的性質之外,還要能知道伽利略所做過的實驗,以及他是「如何看到」這個實驗結果的。所以,與其去問「物體為什麼會有慣性?」不如去問「慣性是甚麼?」、「慣性有哪些特性?」以及「慣性是怎麼被發現的?」
有趣的是,慣性究竟是怎樣的一個觀念,其實困擾了牛頓將近二十年的時間。由於「作用力是造成運動速度的原因」,在當時是個根深蒂固的觀念,所以牛頓最初在整合伽利略的實驗時,曾以為慣性是物體本身所具有的一種「內在趨動力」,使其可以保有原先的運動狀態。他也是花了很長的一段時間,才體認到「慣性不是一種作用力」。所以,在學習的過程中,若我們遇到「不懂」的地方,或是有「矛盾」的感覺,其實是很正常的,而那正是值得我們下功夫去弄懂的地方。
科學史上的許多故事,都告訴著我們,釐清某個觀念是一個漫長,甚至是艱辛的過程,往往也是一個既需要「發現」更需要「發明」的過程。
物理定律DIY
接著,我來介紹一個「物理定律DIY」的方法,當然這不是一個正式的科學名詞,更不是唯一的方法。不過,當我在紐西蘭第一次接觸到這段教學內容時,感覺蠻新鮮,而且也蠻具啟發性的。
台灣大約是從國一或國二開始,而則是紐西蘭從九年級開始,便會介紹所謂的「科學方法」。雖然各家的說法略有差異,但整體上的步驟大致是:發現問題、提出假設、設計實驗、收集數據、分析數據、結論與討論、發表與分享。其中,在設計實驗這個步驟時,學生需要學會如何區分操縱變因、控制變因與應變變因,並據此設計出相關的實驗。
當然,這個所謂的「科學方法」的適用範圍很廣,除了自然科學之外,也適用於社會科學,甚至也可以解答日常生活裡的一些疑問。在物理的實驗課裡,有一個單元是專注在取得變因 (變量) 之間的數學關係式,其中十一年級是要「完成一個具有線性數學關係的物理探究實驗」 (參考前文:紐西蘭物理實驗的評量方式:以虎克定律為例) ,十二與十三年級則是需要「完成一個具有非線性數學關係的物理探究實驗」,而十三年級,還需要考慮數據誤差的分析與計算。
尋找變量之間的函數關係
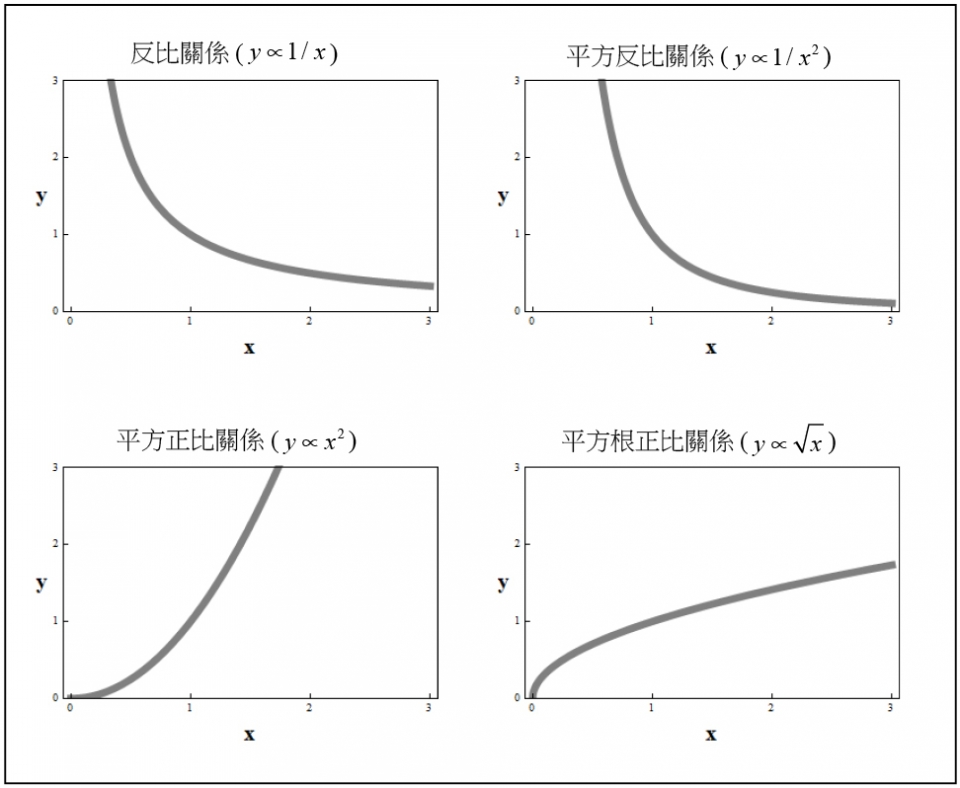
在紐西蘭中學的物理課程裡,所謂的「非線性數學關係」只限於以下這四種基本函數關係 (如圖三所示):
本文以常見的單擺實驗為例,來介紹如何透過實驗的方法 (包含數據分析),來導出「物理定律」,甚至寫下「物理公式」。
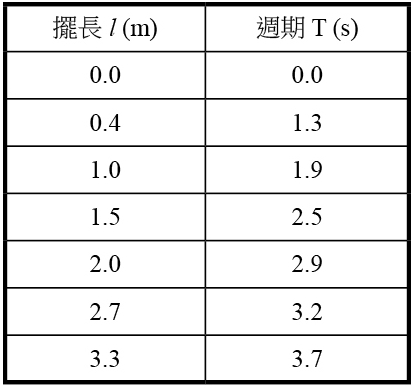
首先,假設我們想知道擺長與週期之間的關係。我們以擺長為操縱變因,而週期則是應變變因 (即實驗觀測的結果) ,其它如擺錘質量、振幅等因素均保持不變,是整個實驗裡的控制變因。
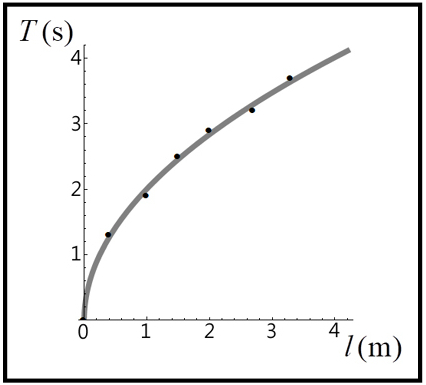
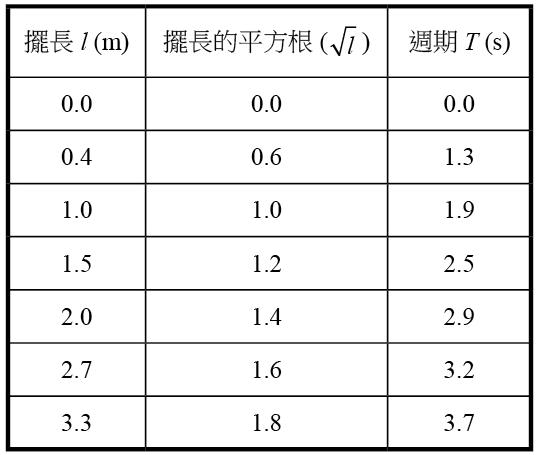
圖四:週期與百長的關係圖;橫軸為擺長 ( l ),縱軸為週期 (T)。圖形顯示二者為平方根正比關係。
表格一為實地測量的數據紀錄。我們以擺長l (操縱變因) 為橫軸,週期 T (應變變因) 為縱軸,繪出的函數關係 (如圖四所示)。與已知的函數關係圖 (圖三) 相對照可以看出,二者之間具有「平方根正比」關係,亦即週期正比於擺長的平方根 ( \(T \propto \sqrt{l}\) )。
根據函數關係來處理數據
在得出這個關係式之後,我們便可進一步處理數據:對擺長開根號 (  )。處理之後的結果如表格二所示。
)。處理之後的結果如表格二所示。
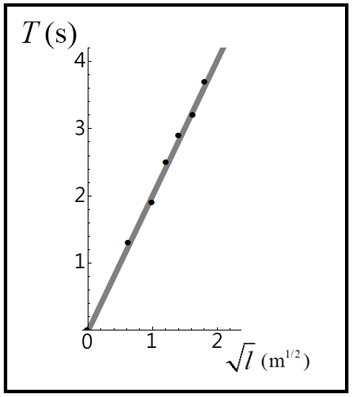
圖五:將橫軸改成擺長開根號之後的數值,重繪週期與擺長平方根之間的函數關係,由圖形可知二者成正比關係
根據表格二的數據,我們以擺長的平方根為橫軸,週期為縱軸,如圖五所示,我們可以得出這二者之間為線性關係,亦即正比關係。也就是說,我們已可初步寫下一條「單擺定律」:
以數學的語言來說,「成正比」或「線性數學關係」就是能寫出斜截式 y=mx+c 其中 m 是斜率,c 是截距。從圖五來看,這條直線通過原點,故截距為零,也就是說,我們可以從這個單擺實驗得出一條數學關係式:
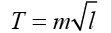
其中最適直線的斜率約為
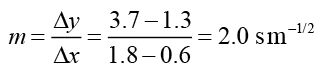
由於截距為零,所以這個斜率也可以看成是週期 ( T ) 與擺長平方根 ( ) 之間的比例常數。
) 之間的比例常數。
假設我們對於單擺運作的物理原理一無所知,我們也能知道它的擺動週期與其擺長的平方根成正比,這就是一條很簡單的物理定律 (或經驗方程式) ,適用於所有小角度振動的單擺:
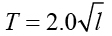
不要輕忽斜率 (常數) 的物理意義
這裡的斜率 (比例常數),以及其它許多的物理常數,往往都有更深一層的含意,除了可以有更精確的實驗測量值之外,也值得我們思考它所具有的物理意義。譬如,在簡諧運動的單元中,我們可以根據牛頓第二運動定律,從自由物體圖分析計算得出,小角度的單擺的振動週期為
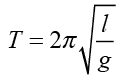
對照我們先前透過實驗所得出來的經驗方程式,式中斜率的物理意義即為 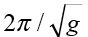 。若重力加速度 g 的理論值9.8 ms-1/2 來看,可得斜率數值為2.007,這可做為對實驗結果的一個驗算,顯示實驗的結果在可接受的範圍。
。若重力加速度 g 的理論值9.8 ms-1/2 來看,可得斜率數值為2.007,這可做為對實驗結果的一個驗算,顯示實驗的結果在可接受的範圍。
然而,若是改從實驗的觀點來看,由於 2π是個常數,因此我們透過實驗所測得的斜率 m,來測量當地的重力加速度大小:
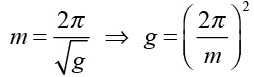
以我們剛剛得出的斜率是2.0 sm-1/2 為例,代入上式可得重力加速度的數值為:
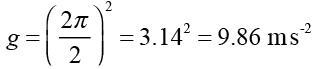
顯然,這個重力加速度也在可以接受的範圍內。更重要的是,透過簡單的單擺實驗,我們便能測量出重力加速度的大小,不是很神奇嗎?
換個單位,換個數值試試看?
現在,我們再回來思考一下克卜勒的「週期定律」。雖然我們現在很熟悉從萬有引力定律與牛頓第二運動定律,以及等速率圓周運動之速率與週期的關係式,透過計算的方式,推導出行星運動的週期定律。
然而,回到科學史的現場,數學家出身的克卜勒是於1619年得出並寫下週期定律,而牛頓則是到了1687年才發表《自然哲學的數學原理》這本巨著,時隔將近七十年。顯然,克卜勒並不知道牛頓,自然也無法以牛頓的方法,來推導出行星運動的週期定律。所以,他是如何想到或猜到「週期平方」與「橢圓軌道的半長軸的三次方」的呢?
當然,我們無法還原克卜勒的心路歷程,但是藉由現代的觀測數據,還是可以稍稍體會一下這個「猜測」的過程。
首先,我們先看看表格三的左半部,數據顯示以「天」為單位的行星公轉週期,和以「百萬公里」為單位的半長軸長 (即行星與太陽之間的平均距離)。雖然數據精確無誤,但卻很難看出有甚麼規律,由此也可以想見克卜勒當年所遭遇的難處。
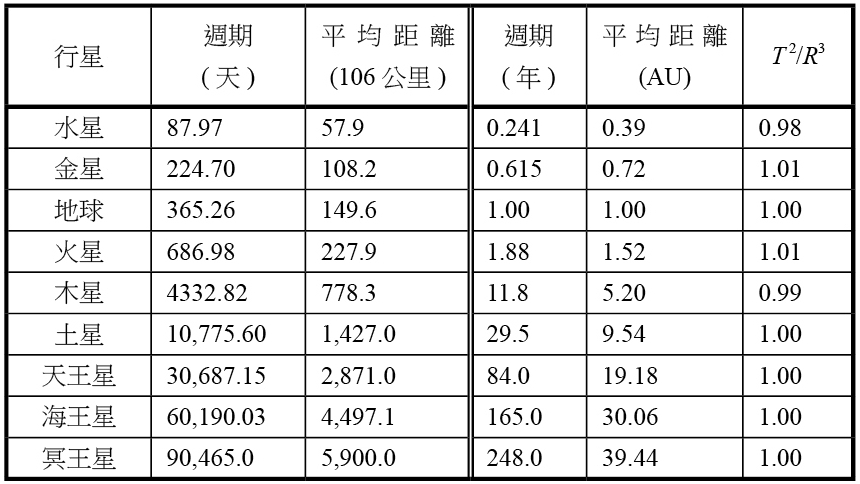
表格三:現代的觀測行星軌道數據 (冥王星於2006年被重新歸類為矮行星。)
然而,如果我們以地球為基準,把週期的單位改成「年」,距離的單位改成AU (Astronomical Unit,天文單位,日地之間的平均距離) , 再把數據改寫在表格的右半部。如此一來,有幾個數值之間的關係,似乎變得比較明顯一些,譬如地球與土星之間,平均距離增加約10倍,而週期則增加約30倍。或是地球與天王星之間,平均距離增加約20倍,週期則增加約85或90倍。
如果我們假設週期與平均距離之間有個乘冪關係,例如:週期 ( T ) 的 x 次方除以平均距離 ( R ) 的 y 次方等於某個定值。
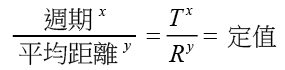
以地球的數值帶入,可得這個定值為1。從土星的數據來看,由於週期的數值大於平均距離的數值,所以 X需小於 y 。讓我們以嘗試錯誤的方法,以 x=1、y=2 來試試看:
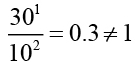
結果發現它不等於1。再以 x=2、y=3 代入:
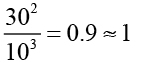
這個結果讓我們對平方與立方的選擇,有了些許的信心。接著,我們把表格中的數據,代入最新的這個關係式中,結果寫在表格最右方的欄位 ( T2/R3) 中,我們驚喜地發現到,所有行星的週期與軌道平均半徑竟然都滿足這個關係式!
雖然我們在此只用了簡短的幾個字,就正確地「猜測」出這個定律,但是別忘了,克卜勒當初可是用了將近十年的時間,才得出這個規律。
當我們看到行星繞日現象背後竟然有著如此簡潔的規律之後,是否不禁讓人感到好奇,而想去追問為什麼?而解答這個問題的人,就是我們所熟知的牛頓。
結語:物理定律並非遙不可及,你自己也能DIY
我們以克卜勒行星運動定律與慣性定律為例,分別從定性與定量的角度,強調了「定律是實驗或觀測的結果」,而得出這樣的結果,往往是一個「發現」與「發明」兼而有之的過程,所以,當我們看到物理定律時,首先要弄清楚的是,這個定律所描述的是怎樣的一個「自然現象」,而科學家又是透過怎樣的實驗或觀察而得出這個定律?之後再來思考存在於這個定律背後的的可能原因。
最後,我們除了學習前人所發現的物理定律之外,對於有興趣或趕到疑惑的自然現象,也可以大膽假設、小心提問,據此來設計實驗或觀察的方法,去DIY,寫下由你自己發現或發明的物理定律。
參考資料
OpenStax. (2017) . 3.1 The Laws of Planetary Motion. https://ucf.pb.unizin.org/astronomybc/chapter/3-1-the-laws-of-planetary-motion/