拓樸超導體

  • 物理專文
  • 撰文者：莊天明、陳鵬仁、關旭佑
  • 發文日期：2017-09-26
  • 點閱次數：2721
Print   PDF

 拓樸超導體是一種特別的物質。顧名思義，它擁有一般超導體的性質，例如完整的超導能隙 (superconducting gap, tien f1 )。然而不同於一般超導體的是其超導庫柏電子配對 (Cooper pair) 具有手性 (chirality)，如同拓樸絕緣體的表面電子態具有手性。而手性超導配對的一項重要特性就是在邊緣或是缺陷處會有馬約拉納(Majorana) 準粒子束縛態的存在。馬約拉納費米子 (fermion) 是一種本身為自己反粒子的費米子。因此，當兩個馬約拉納費米子在一起時就會互相消滅而無法探測。在基本粒子理論，微中子可能是個馬約拉納費米子，但是實驗還無法確認這個預測。在凝態物理的拓樸超導體中，兩個馬約拉納準粒子可以在相離很遠的邊緣或缺陷處各自存在，因此有機會被探測到。例如我們施加磁場在超導體這樣符合電子─電洞對稱 (particle-hole symmetry) 的系統中，馬約拉那準粒子會被束縛在超導渦旋 (vortex) 的零能量處，實驗即可量測到零偏壓時導電率的峰值 (zero bias conductance peak)，而這也是拓樸超導體的一個重要現象。馬約拉納束縛態不會被外界干擾而退相干 (decoherence)，此特性可應用於容錯性量子計算，因此探測馬約拉納準粒子是目前凝態物理的關注焦點之一。

    傳統s-wave超導體中的庫柏電子對是由兩個自旋相反的電子形成的自旋單重態 (spin singlet)，因此s-wave超導體中的Bogoliubov準粒子並不符合本身為自己反粒子的條件。如果庫柏電子對為自旋三重態 (spin triplet)，那麼庫柏電子對中的兩個電子將可具有同方向的自旋 (可稱之無自旋)，便可解決這個問題。這樣的庫柏電子對會可具有p-wave對稱性。也因此拓樸超導體中最簡單的型態之一為手性無自旋p-wave超導體，但是到目前為止，物理學家還沒有確認任何超導體具有這樣的超導對稱性，雖然很多物理學家猜測SrRuO4可能是三維手性p-wave超導體，然而，時間反轉對稱在手性p-wave超導體中理應被超導波函數中軌域項所產生的磁矩所破壞。但是此特性在SrRuO4中尚未被實驗所確認。此外，SrRuO4超導溫度僅有1.5K，也增加了實驗的難度，因此尚不能確定它是拓樸超導體。

    既然在自然界中的p-wave超導體如此稀有，那只有試著用一些特別的方法實現拓樸超導體了。主要的原則是結合自旋極化 (spin polarized) 電子和超導這兩個性質，實驗的方向可區分為下列幾類：(1) 一維磁性原子放置在s-wave超導體上、(2) 拓樸絕緣體與s-wave超導體的異質結構 (heterostructure)、(3) 反常量子霍爾效應 (quantum anomalous Hall effect) 與超導體的異質結構、(4) 一維半導體奈米線與s-wave超導體的異質結構、(5) 摻雜拓樸絕緣體使其發生超導性、(6) 同時具有超導與拓樸表面態的化合物。以下我們簡單介紹這些理論與目前實驗的進展。

一維鐵磁性原子鏈放置在超導體上：

    如果將磁性原子放置於s-wave超導體上，由於庫柏電子對與磁性原子自旋的交互作用，在超導能隙中會產生自旋極化的Shiba束縛態。如果將磁性原子排成一列，磁性原子鏈中的Shiba束縛態會形成自旋極化能帶並恰好通過超導體的費米能階，如此一來可以形成p-wave拓樸超導體，而磁性原子列的兩端會束縛著馬約拉納準粒子[1][2]。具有原子解析度的低溫掃描式穿隧顯微鏡 (Scanning tunneling microscope, STM) 最適合來進行這種實驗。美國普林斯頓大學的Yazdani團隊[3]將少量鐵原子蒸鍍在具有強電子自旋軌域偶合的s-wave超導體鉛的表面後，再找尋表面上的鐵原子鏈作探測。於T=1.6K或更低的20mK時，他們發現在鐵原子鏈的末端，有明顯的零偏壓導電率峰值。如上所述，這是馬約拉納束縛態的一個特徵。而在鐵原子鏈的中段，就沒有發現到這樣的零偏壓導電率峰值。雖然他們的實驗觀察到與理論預測相吻合的邊界態，然而由於他們樣品的鐵原子鏈結構為Z字形，所以在超導能隙內出現較複雜的Shiba束縛態。另外此實驗中的原子鏈長度遠小於鉛的超導相干長度 (coherence length)，因此邊界兩端的馬約拉納束縛態有機會互相混成而形成一般費米子。未來解決方法之一是直接利用STM操控鐵原子在鉛表面的位置，排列成更線性且更長的一維原子鏈。

 

1
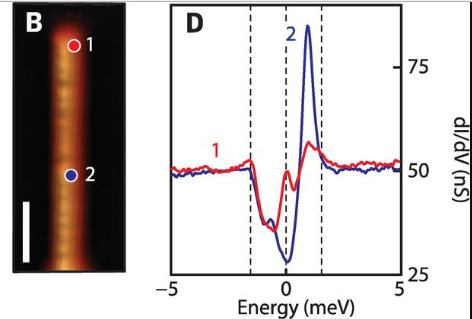
左圖:蒸鍍於鉛表面上的鐵原子鏈。右圖：於鐵原子鏈邊緣 (位置1) 與中間 (位置2) 測量到的微分電導率 (differential conductance, dI/dV)，只有在鐵原子鏈邊緣時，才有零偏壓峰值。[3]

 

二維拓樸絕緣體與s-wave超導體的異質結構

Fu與Charles Kane提出了一個簡單方法來產生架構拓樸超導體所需的自旋極化電子能帶[4]。根據他們的理論研究，如果把一個s-wave超導體放在3D拓樸絕緣體之上，藉由鄰近效應 (proximity effect) 將拓樸絕緣體的自旋手性表面態變成超導態，這樣兩者的介面就會產生二維手性p-wave超導體。根據這個模型，北京清華大學薛其坤團隊[5]在s-wave超導體的表面上鋪上單層Bi後，再蒸鍍上不同層數的拓樸超導體Bi2Se3，他們發現在蒸鍍6層Bi2Se3後，Bi2Se3表面可以用角分辨光電NbSe2子能譜 (ARPES) 觀察到拓樸表面態，利用低溫STM也可以測量到超導能隙。利用類似的Bi2Te3/NbSe2異質結構，上海交大賈金鋒團隊利用STM在T=0.4K測量到了磁場下超導渦流中心的零偏壓導電率峰值，同時他們也發現此E=0之束縛態可在超導渦流內部維持相當長的距離[6]。雖然理論上超導渦流中心可能會有馬約拉那束缚態的產生，然而NbSe2為第二類超導體，其超導渦流中心在磁場下也會具有一般的束缚態 (E ¹0)，這兩種束縛態的能量需要有f2的解析度，在T=0.4K時STM因為熱效應最高僅有~0.1meV的能量解析度，因此目前尚無法確定馬約拉那束缚態是否存在於此系統的超導渦流中心。

 
23p22p23

 
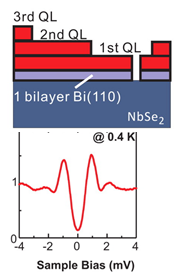
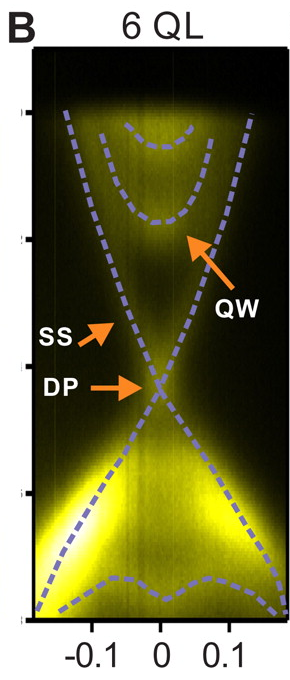
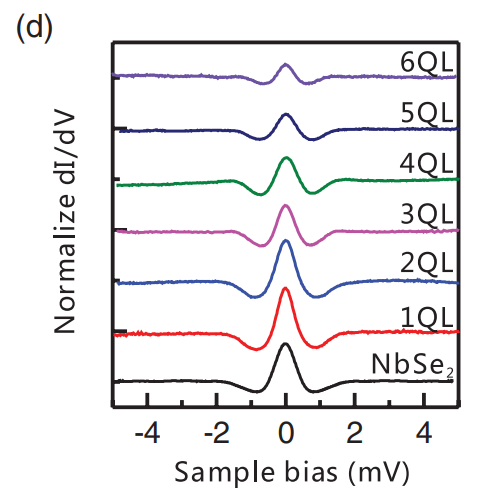
左上圖：拓樸絕緣體/超導體示意圖。以超導體NbSe2為基底，上面覆蓋數層的Bi2Se3。左下圖：當覆蓋6層Bi2Se3時，可在表面量測到利用鄰近效應所產生的超導能譜。中圖：以角分辨光電子能譜 (ARPES) 測量覆蓋6層的Bi2Se3，顯示出狄拉克錐 (Dirac cone) 的能帶，這是拓樸絕緣體的特徵之一。右圖：在Bi2Se3/NbSe2的結構上，可以於超導渦流中測量到零偏壓導電率峰值。[5][6]

 

反常量子霍爾效應與超導體的異質結構

拓樸超導體所需要的手性，也可以由具有量子霍爾效應的物質來提供。具有量子霍爾效應的物質便是一種二維的拓樸絕緣體，在外加磁場下，於物質的邊緣將有手性的電流產生。不過外加磁場多會減弱超導特性。因此，史丹佛大學張首晟團隊便提出理論構想，利用不需要外加磁場，本身即內建磁矩的反常量子霍爾效應材料與超導體的異質結構來產生手性的馬約拉納準粒子[7]。要產生反常量子霍爾效應的做法是將磁性原子摻雜入拓樸絕緣體中[8]。最近UCLA的王康隆團隊將Nb超導體鍍在具有反常量子霍爾效應的 (Cr0.12Bi0.26Sb0.62)2Te3上。他們觀測到了明確的e2/2h的電導率平台，而且其電導率與磁場的關係與理論預測相符[9]。而論文中進行的控制實驗也排除了一些其他的解釋。然而馬里蘭大學的理論學家Jay. D. Sau對此電導率平台提出另外的解釋，認為是反常量子霍爾效應物質內部的無序擾亂 (disorder) 而造成[10]，因此未來實驗上還需排除這種可能性。

P31P32
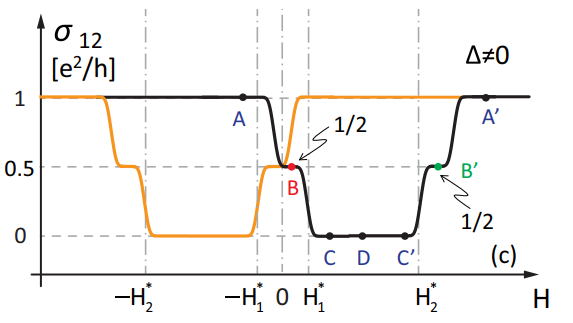
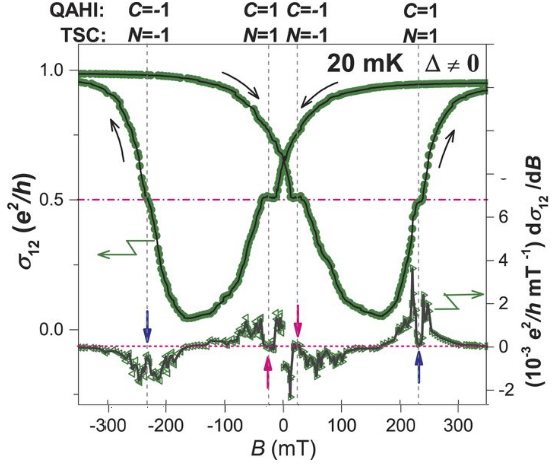
左圖為理論預測，超導體置放於反常量子霍爾效應物質上，電導率與外加磁場的關係。右圖為實驗結果，兩者相當吻合。[7][9]

 

一維半導體奈米線與超導體的異質結構

    理論上可利用拓樸絕緣體的自旋手性與超導電子對組成拓樸超導體，而具有自旋手性的物質不僅限於拓樸絕緣體而已，具有強自旋軌道耦合 (spin-orbit coupling) 的材料多有這樣的特性。R. M. Lutchyn等人提出了一個模型[11]，利用有Rashba效應的強自旋軌道耦合半導體作為自旋手性的基底後再放上超導體。但不同於拓樸絕緣體於一個表面只有單一方向的手性，Rashba半導體在同一能量下具有順時針和逆時針的手性，因此需要引進Zeeman效應 (加上磁性物質或是水平磁場) 以分裂其能帶 (如下圖)。之後再調整費米能階，使超導能隙的能量正好落在其中一個手性能帶上，便能得到拓樸超導體。荷蘭Delft大學的Kouwenhoven團隊製備了具Rashba效應的InSb半導體奈米線與超導體的元件，並施加水平磁場與改變閘極的電壓以調控費米能量。他們測量到零偏壓電導率峰值，而且這峰值在一定的磁場範圍下不隨著磁場改變，符合馬約拉納束縛態的特性[12]。然而製備元件的過程中，如果摻雜了些微的磁性雜質，在低溫下磁性雜質對電子所產生的近藤效應（Kondo effect）也會產生零偏壓電導率峰值，因此如何排除這個因素，是確認馬約拉納束縛態的關鍵。

 

p55
 

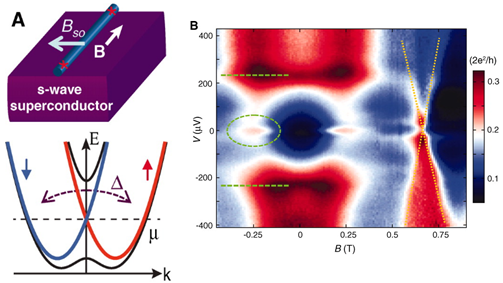
左上圖：將強自旋軌道耦合半導體奈米線放在s-wave超導體上，再加以方向與自旋軌道耦合等效磁場垂直的水平磁場。左下圖：因為Rashba效應而自旋分裂的能帶(紅線與藍線代表不同的自旋極性) 。加上水平磁場後便會使其能帶分裂 (黑線所示)，費米能量為虛線的位置。右圖：測量電導率發現在特定的磁場範圍有零偏壓的峰值(綠色圓虛線)，這個峰值若改變水平磁場至平行自旋軌道耦合等效磁場的等效方向時，便會消失。[12]

 

摻雜拓樸絕緣體使其發生超導性

將拓樸絕緣體摻雜一些其他原子，使其產生超導性，理論上可以直接得到拓樸超導體。Hor等人以銅原子摻雜了被廣泛研究的拓樸絕緣體Bi2Se3，發現在T=3.8K會產生超導[13]，稍後ARPES實驗也顯示了樣品表面的拓樸能帶仍然存在[14]。雖然在點接觸 (point contact) 的測量中有得到零電壓導電率峰值[15]，同時核磁共振NMR實驗也觀測到p-wave超導體所應具有的自旋旋轉對稱性破壞[16]。然而低溫STM實驗卻顯示這類樣品在奈米尺度下非常不均勻，只有某些區域會形成超導態[17]。而在超導渦流中，也沒有發現零電壓導電率峰值[17]。最近北京中科院丁洪與東京大學Shik Shin團隊也發現鐵基超導體FeTe0.55Se0.45具有表面拓樸能帶，由於具有較高的Tc~14.5K因此可提供另一個研究拓樸超導的材料[18]，雖然還有待進一步實驗確認。但是對這類原子摻雜的樣品而言，製備均勻性以及是否影響到巨觀量測結果是個極為關鍵的問題。
 

P61P62
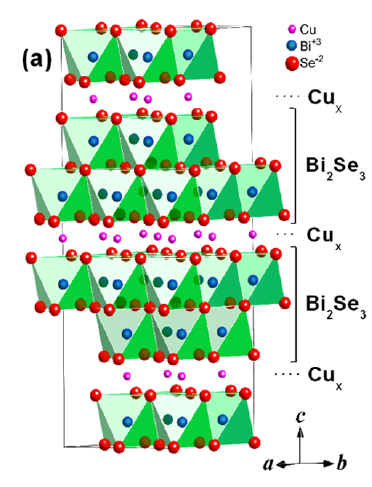
左圖：摻雜銅原子的CuxBi2Se3的晶體結構。右圖：點接觸實驗測量到零偏壓電導率峰值。 [13][15]

 

 同時具有超導與拓樸表面態的化合物

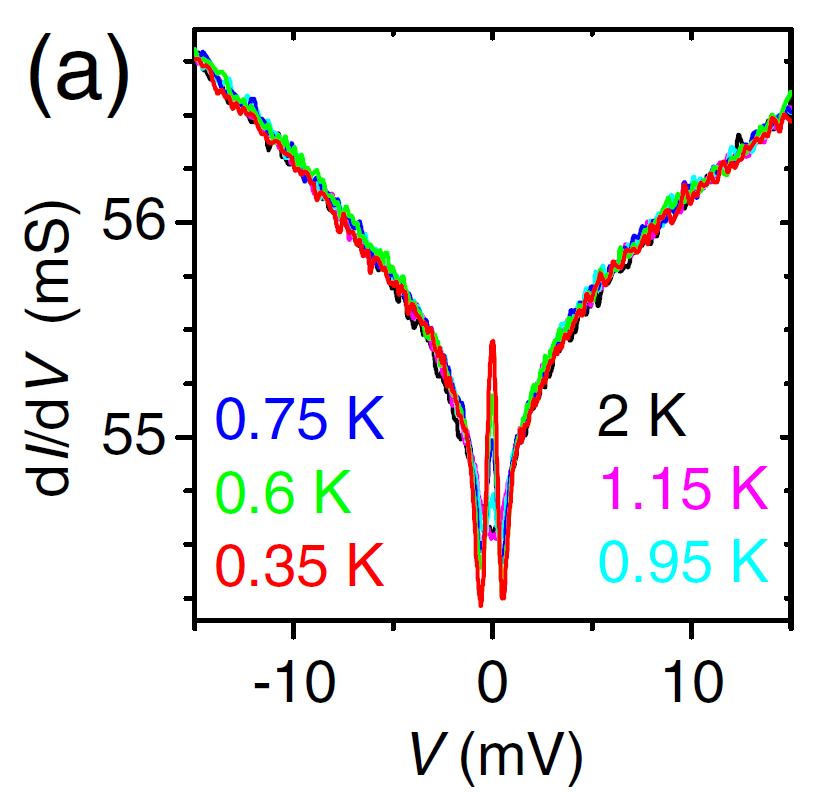
    由於人工產生的拓樸超導體多為摻雜、多層薄膜或原子排列的結構，於實驗上的控制有其困難性，因此物理學家想尋找符合簡單化學配比且有塊材的超導性質，又有拓樸表面態的化合物。這樣的化合物將具有較穩定的材料性質，更能夠符合應用。最近我們中研院團隊與台大周方正老師、清大鄭弘泰老師合作發現的PbTaSe2超導體就是第一個符合簡單化學配比 (stoichiometric) 的拓樸材料[19]。PbTaSe2塊材的量測顯示出其為s-wave超導體 (Tc~3.8K)，而第一原理計算顯示出PbTaSe2具有拓樸表面態且此自旋極化能帶通過費米能階，降溫到超導態時可形成手性p-wave超導[19, 20]。我們利用自製低溫STM進行準粒子干涉 (quasiparticle scattering interference, QPI) 影像實驗量測到與拓樸表面能帶相符合的結果。同時在低溫T=0.26K時也解析出完整的超導能隙，顯示拓樸表面能帶確實形成超導。此外，我們也利用STM於磁場下可以清楚觀測到超導渦流，並且渦流中心量測到零偏壓導電率峰值。然而如前面所述，在T=0.26K要解析出馬約拉納束縛態需要0.01meV的能量解析度，因此PbTaSe2超導渦流中的零偏壓導電率峰值的物理意義仍然需進一步確認。最近日本RIKEN的Tetsuo Hanaguri團隊也發現BiPd2超導體 (Tc~5.4K) 中也具有拓樸電子極化表面態[21]，提供第二個可能實現拓樸超導的簡單化學配比材料。

 

p4

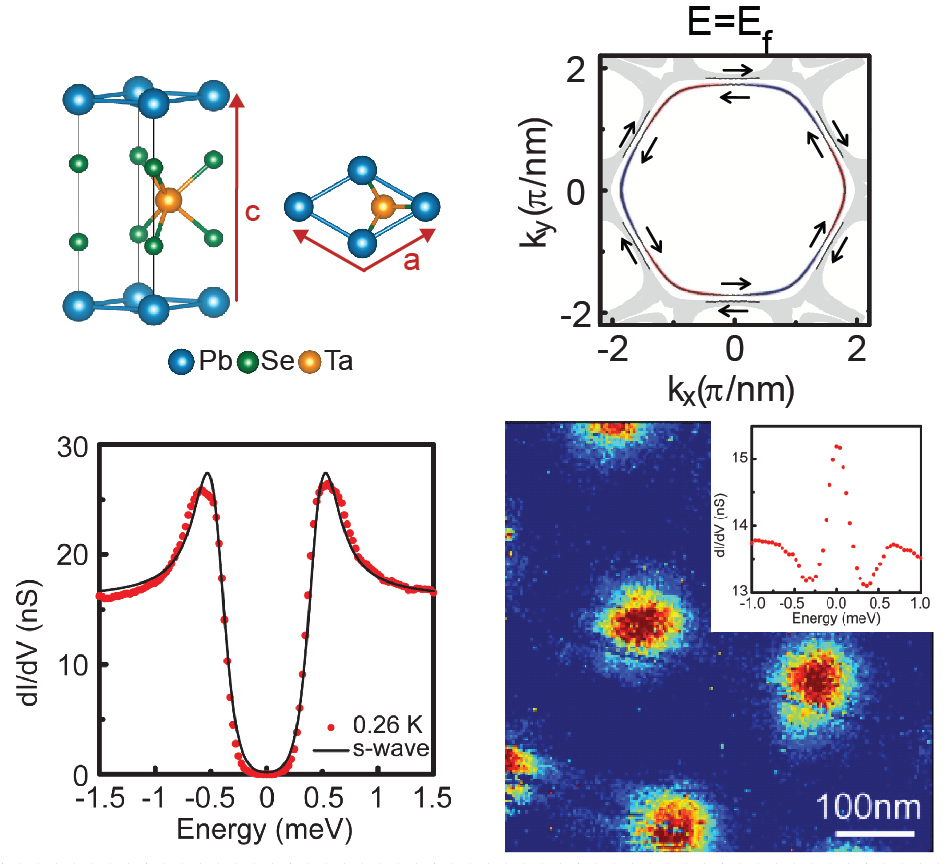
左上圖： PbTaSe2晶體結構。右上圖：理論預測於費米能量上的能帶結構。左下圖：利用低溫STM於 T=0.26K下解析出完整的超導能隙，顯示拓樸表面能帶形成超導。右下圖：於T=0.26K與磁場0.05T下的渦流晶格，其中內圖為於渦流中心測量到的零偏壓電導率峰值。 [19]

本文簡單介紹了拓樸超導體的一些理論模型和目前實驗的進展。雖然許多實驗都有量測到零偏壓導電峰值，也有測量到電導率平台e2/2h，然而這些現象是否為馬約拉納費米子所造成，以及其他理論預測的拓樸超導體性質，如反常的約瑟夫電流、量子化的霍爾熱導率等等仍還需進一步實驗驗證[22]，以期達成未來應用拓樸超導體的目標。

還可以閱讀：拓樸絕緣體之能帶結構、輸運性質與場效電晶體元件之介紹與研究，拓樸材料與拓樸能帶理論，2016年諾貝爾物理學獎：相變與拓樸相變介紹，拓樸物質的理論研究發現，自旋角動量：從愛因斯坦-德哈斯實驗講起，磁性薄膜中之磁矩方向操控

​​​​​​​

參考資料：

  1. A. Y. Kitaev Phys. Usp. 44, 131 (2001).
  2. S. Nadj-Perge et al., Phys. Rev. B 88, 020407(R) (2013)
  3. S. Nadj-Perge et al., Science 346, 6209, 602 (2014)
  4. L. Fu and C. Kane, Phys. Rev. Lett. 100, 0964078 (2008)
  5. M.X Wang et al., Science 336, 52 (2012)
  6. J. P. Xu et al., Phys. Rev. Lett. 112, 217001 (2014)
  7. J. Wang et al., Phys. Rev. B 92, 064520 (2015)
  8. C. Z. Chang et al., Science 340, 167 (2013)
  9. Q. L. He et al., Science 357, 294 (2017)
  10. Y. Huang et al., arXiv:1708.06752 (2017)
  11. R. M. Lutchyn et al., Phys. Rev. Lett. 105, 077001 (2010)
  12. V. Mourik et al., Science 336, 1003 (2012)
  13. Y. S. Hor et al., Phys. Rev. Lett. 104, 057001 (2010)
  14. L. A. Wray et al., Nat. Phys. 6, 855 (2010)
  15. S. Sasaki et al., Phys. Rev. Lett. 107, 217001 (2011)
  16. K. Matano et al., Nat. Phys. 12, 852 (2016)
  17. N. Levy et al., Phys. Rev. Lett. 110, 117001 (2013)
  18. P. Zhang et al., arXiv:1706.05163 (2017)
  19. S. Y. Guan et al., Sci. Adv. 2, e1600894 (2016)
  20. T. R. Chang et al., Phys. Rev. B 93, 245130 (2016)
  21. K. Iwaya et al., arXiv:1708.08204 (2017), accepted in Nat. Comm.

[22] C. W. J. Beenakker, Ann. Rev. Cond. Mat. 4, 113 (2013)