
拓樸絕緣體之能帶結構、輸運性質與場效電晶體元件之介紹與研究
- 物理專文
- 撰文者:黃榮俊 (國立成功大學物理系教授)
- 發文日期:2017-09-27
- 點閱次數:3047
傳統上,物質的狀態分類主要是依循原子對稱性破壞的原理,如晶體、多晶體與非晶體。從宏觀電性來說,物質可以大致簡單分為三類:導體、絕緣體跟半導體。量子霍爾態 (Quantum Hall state) 在西元1980年被發現,提供了新物質態-量子態的第一個特例。它沒有自發地斷開原子對稱性,然而其電子結構與輸運行為僅取決於其拓樸性 (topology) [1]。本質自旋霍爾效應 (Intrinsic Spin Hall Effect) 的理論在2003年被提出[2][3],說明物質中自旋的分離是因為物質的本質能帶結構造成的,引發了大家對於能帶以及自旋電流研究的興趣。雖然當時最根本的原因尚未確認,但卻埋下了大家對於量子版本的自旋霍爾效應猜測的種子。美國理論學家C. L. Kane及E. J. Mele在2005年提出石墨烯 (graphene) 是具有量子自旋霍爾效應 (Quantum Spin Hall Effect) 的一種材料[4]。他們認為石墨烯微小的能隙會因為自旋軌道耦合 (Spin-orbital coupling, SOC) 的效應而打開,進而變成絕緣體;此外其邊緣態 (Edge states) 也會出現於能隙中。這樣的行為和量子霍爾效應是非常像的,然而這不需要一個外加的磁場。
造成量子自旋霍爾效應的主因在於自旋軌道耦合以及塊體材料的能隙,其霍爾電導值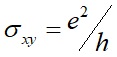 。B.A. Bernevig和史丹福大學張守晟在2006年提出了另一個擁有量子自旋霍爾效應的材料-碲化汞[5],他們提出了觀察碲化汞量子井的方式。在一年內,德國Würzburg大學中的Molenkamp實驗室就建構了一套系統來觀察這種特殊的效應[6]。Kane和Mele引進了拓樸不變量Z2 (topological Z2 invariant) [7]來描述正常以及特殊能帶結構的絕緣體。非零的Z2量之邊緣態遵守了時間反演對稱性 (time-reversal symmetry),使其能帶結構是非常穩定且不易破壞的。擁有這類特性的材料就被稱之為「拓樸絕緣體 (topological insulators, TIs)」,這種新型態的能態只建立於它自身的拓樸性。有趣的是,拓樸絕緣體雖然在內部與其他絕緣體沒有差別,但在其邊緣 (二維拓樸絕緣體) 或表面 (三維維拓樸絕緣體) 則是呈導體的性質,因此這種特殊的電子能態也稱之為邊緣態/表面態。
。B.A. Bernevig和史丹福大學張守晟在2006年提出了另一個擁有量子自旋霍爾效應的材料-碲化汞[5],他們提出了觀察碲化汞量子井的方式。在一年內,德國Würzburg大學中的Molenkamp實驗室就建構了一套系統來觀察這種特殊的效應[6]。Kane和Mele引進了拓樸不變量Z2 (topological Z2 invariant) [7]來描述正常以及特殊能帶結構的絕緣體。非零的Z2量之邊緣態遵守了時間反演對稱性 (time-reversal symmetry),使其能帶結構是非常穩定且不易破壞的。擁有這類特性的材料就被稱之為「拓樸絕緣體 (topological insulators, TIs)」,這種新型態的能態只建立於它自身的拓樸性。有趣的是,拓樸絕緣體雖然在內部與其他絕緣體沒有差別,但在其邊緣 (二維拓樸絕緣體) 或表面 (三維維拓樸絕緣體) 則是呈導體的性質,因此這種特殊的電子能態也稱之為邊緣態/表面態。
Kane和他的學生Liang Fu在2007年預測了Bi1-XSbX這類的化合物也會有拓樸表面態的性質[8],而普林斯頓大學的Zahid Hasan團隊利用了角分辨光電子能譜 (Angle Resolved PhotoEmission Spectroscopy, ARPES) 的分析來證明了這個事實[9]。隨後大陸中科院的Zhong Fung與張守晟合作,並預測了V2VI3 材料中的Bi2Se3、Bi2Te3、Sb2Te3都是三維的拓樸絕緣體,(但Sb2Se3卻不是),如圖一所示[10]。而這些三維拓樸絕緣體的表面態特性都在2009年被ARPES量測出來[11][12]。
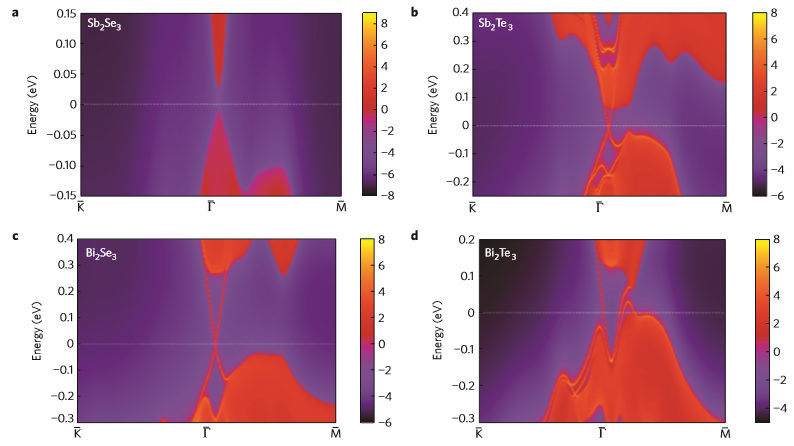
圖一 (a) Sb2Se3 (b) Sb2Te3 (c) Bi2Se3 (d) Bi2Te3的能帶理論計算[10]
拓樸絕緣體的能帶結構與輸運特性介紹
雖然二維拓樸絕緣體的理論預測早於三維拓樸絕緣體,但在實驗上的研究卻是比較少的。至今碲化汞量子井仍然是唯一被實驗證實有量子自旋霍爾效應的二維材料。然而,碲化汞量子井在本質二維材料的特性中是難以像石墨烯一樣觀測此效應的,再者其塊體 (bulk) 的能隙太小了,導致其量子自旋霍爾效應只能在非常低溫的條件下觀察到。
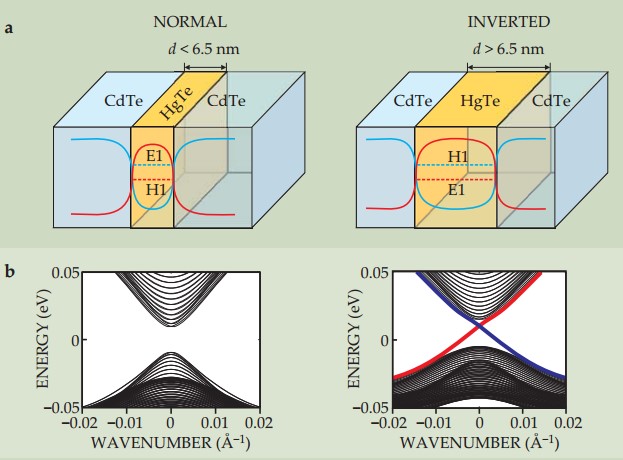
圖二 量子自旋霍爾邊緣態的出現和碲化汞層的厚度有關,實驗顯示當碲化汞厚度大於6.5nm時,量子井會形成一種二維拓樸絕緣體[14]
當碲化汞的薄膜超過一個特定的厚度時,碲化汞的量子井會形成一種拓樸絕緣體[5]。這個系統中的自旋軌道耦合效應是夠強到產生價帶分裂,其中能量較高的能帶會進而變成s波的導帶。圖二顯示了碲化汞-碲化鎘系統之下的能譜示意圖[14],當碲化汞的厚度大於6.5nm時,帶著相反自旋的邊緣態將會出現,此時的量子井具有量子化電阻率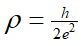 ,或電導是
,或電導是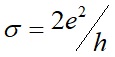 [6][14][15]。
[6][14][15]。
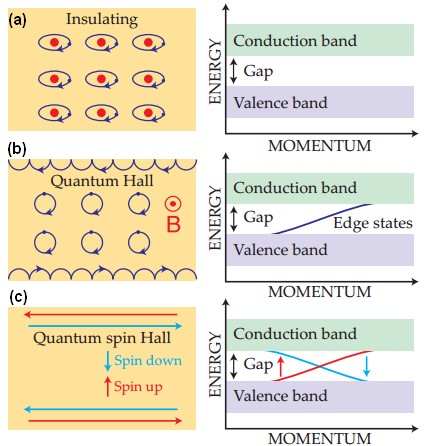
圖三 不同的電子能態及其對應圖(a) 絕緣體 (b)量子霍爾效應 (c)量子自旋霍爾效應[14]
/h加上2/h:藍色「自旋向下」帶的頂部的e2/h為單位。然而在量子自旋霍爾效應中 (圖三(c)),電導卻是2e2圖三說明了不同拓樸性的電子態。在量子霍爾效應中 (圖三(b)),邊緣態的電導是量子化的,以e
三維拓樸絕緣體的表面態也是源於自身材料的強自旋軌道耦合。以一般的半導體來說,價帶 (Valence band) 的產生來自p軌域的電子貢獻,導帶 (Conduction band) 產生來自s軌域的電子貢獻。然而對於質量較大的元素,由於自旋軌道耦合比較強,導致p軌域的能帶可以跑到了s軌域的能帶上方,造成能帶倒置(Band inversion) [14]。
二維(2D)拓樸絕緣體的拓樸絕緣體的邊緣態和三維(3D)拓樸絕緣體的表面態受到時間反演對稱性的保護,其表面態的載子若落在塊材的能隙之中,則這些電子的動量與自旋維持一定方向鎖定關係(Spin-Momentum Locking, SML),意即電子的行進方向決定了自旋的方向,這也是本質自旋流造成的原因。由於邊緣態/表面態被時間反演對稱性的保護,導致其不受雜質以及幾何結構缺陷的影響,強烈地抑制了背向散射(back scattering),所以其輸運傳導是高度金屬性的[15]。這些因素造成拓樸絕緣體在先進自旋電子學元件之研究和應用上扮演非常重要的角色。
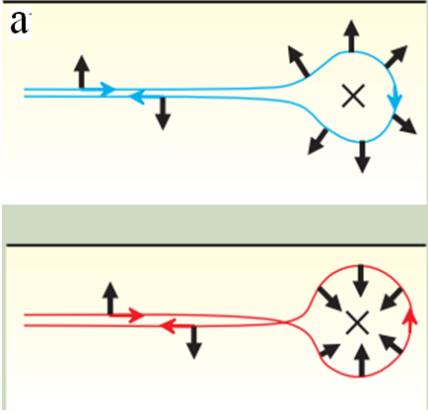

圖四 (a) 量子自旋霍爾效應的邊緣態/表面態,由於時間反演對稱性,電子經由兩種不同路徑會產生 相位差,造成了破壞性干涉。 (b) 邊緣態/表面態在外加磁場下表現出弱局域化效應 (WAL)。[15]
相位差,造成了破壞性干涉。 (b) 邊緣態/表面態在外加磁場下表現出弱局域化效應 (WAL)。[15]
圖四 (a) 簡單地圖解說明在邊緣態/表面態電子之非磁性雜質的背向散射是不被允許的。處在量子自旋霍爾效應的邊緣態/表面態的電子,遇到雜質時會經由順時針或是逆時針的機制被散射,這兩個反向路徑個別會有相位 或是-
或是- 的相位,同時發生的時候則會形成一種量子干涉效應。量子系統中若存在時間反演對稱性,當電子路徑的相位差為
的相位,同時發生的時候則會形成一種量子干涉效應。量子系統中若存在時間反演對稱性,當電子路徑的相位差為 時,這兩個路徑的波函數是呈破壞性干涉的,導致邊緣態/表面態的電子不會因雜質產生背向散射,也造成了拓樸絕緣體表面態良好的傳導性質。而當外加磁場時,破壞了SML及時間反演對稱性,使背向散射的機率增加,所以電導會下降(電阻率上升),這種傳輸行為就是所謂弱侷域化效應(Weak-AntiLocalization, WAL),如圖四(b)所示。但是在一般的材料中,電子在這兩個反向路徑同時發生的時候則會形成一種建設性干涉,呈現侷域化的行為(weak localization, WL);而當外加磁場時,這種建設性干涉會被抑制,所以電導會上升(電阻率下降)。
時,這兩個路徑的波函數是呈破壞性干涉的,導致邊緣態/表面態的電子不會因雜質產生背向散射,也造成了拓樸絕緣體表面態良好的傳導性質。而當外加磁場時,破壞了SML及時間反演對稱性,使背向散射的機率增加,所以電導會下降(電阻率上升),這種傳輸行為就是所謂弱侷域化效應(Weak-AntiLocalization, WAL),如圖四(b)所示。但是在一般的材料中,電子在這兩個反向路徑同時發生的時候則會形成一種建設性干涉,呈現侷域化的行為(weak localization, WL);而當外加磁場時,這種建設性干涉會被抑制,所以電導會上升(電阻率下降)。
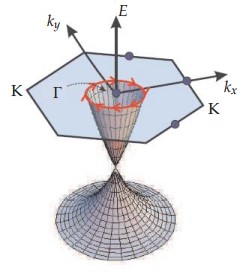
圖五 三維拓樸絕緣體Bi2Se3的在動量-能量空間的狄拉克錐示意圖[15]
量子自旋霍爾能態通常在三維拓樸絕緣體之表面態中都會出現,其中也包含了二維無質量的狄拉克費米子 (Dirac fermions),又因為其分散的形式成為一錐狀,因此三維拓樸絕緣體之表面態也被稱為狄拉克錐 (Dirac cone),如圖五所示。和二維拓樸絕緣體原理之邊緣態相似,三維拓樸絕緣體表面態是受到時間反演對稱性保護的。紅色箭頭表示其表面態的自旋方向,是垂直於其動量的方向。
三維拓樸絕緣體之晶體結構與能帶結構之異同
V2VI3 材料中的Bi2Se3、Bi2Te3、Sb2Te3都是三維拓樸絕緣體。它們的晶體結構非常相似,皆為菱形六面體 (rombohedral) 結構,在c軸方向為六方最密堆積的週期堆積結構,屬於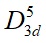 (
(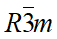 )空間群[16]。其中紅色方框內的五層原子構造為V2VI3著名的Quintuple Layer (QL) 結構:其最大的特點是,在QL內的原子層之間作用力非常的強,可是QL之間的作用力卻是較弱的凡得瓦力,1QL的厚度約為1nm (10
)空間群[16]。其中紅色方框內的五層原子構造為V2VI3著名的Quintuple Layer (QL) 結構:其最大的特點是,在QL內的原子層之間作用力非常的強,可是QL之間的作用力卻是較弱的凡得瓦力,1QL的厚度約為1nm (10 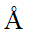 )[10]。以圖六Bi2Se3的晶體構造為參考,a軸及b軸的晶格常數約為4.4
)[10]。以圖六Bi2Se3的晶體構造為參考,a軸及b軸的晶格常數約為4.4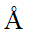 ,c軸約為30
,c軸約為30 
。
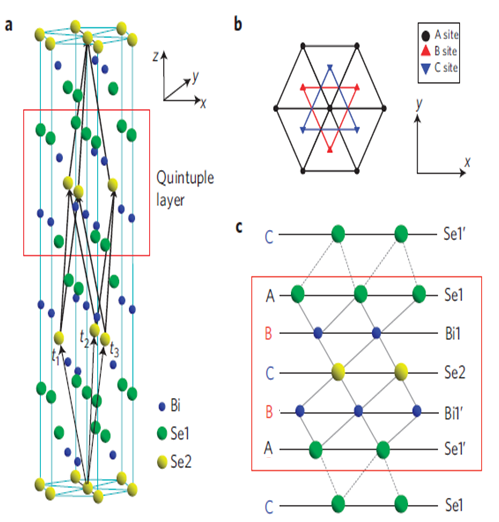
圖六 Bi2Te3的晶體結構。(a) 其原始晶格向量為t1、t2及t3。紅色方框內的Se1–Bi–Se2–Bi–Se1 五層原子為一個Quintuple Layer 結構。(b) 從z軸俯視的示意圖。(c) Quintuple Layer 結構的側面示意圖。[10]
雖然Bi2Te3和Sb2Te3的晶體結構與晶格常數和Bi2Se3非常相似,但是三者的能帶結構卻差異頗大 (圖一)。狄拉克錐的交叉點稱之為狄拉克點 (Dirac Point, DP)。Bi2Te3的DP位於價帶裡面,實驗不易觀察;Sb2Te3的DP位於能隙中間,但其能隙較小 (~ 0.2 eV)。在塊材中Sb2Te3的費米能階EF都位於能隙中間或下方,屬於p型材料 (輸運載子以電洞為主)。Bi2Se3的DP也位於能隙中間,其EF則位於導帶或能隙上方,屬於n型材料 (輸運載子以電子為主) ,且其能隙相對較大 (~ 0.3 eV)。本文以下內容以Bi2Se3為主之三維拓樸絕緣體薄膜和元件做作為研究討論主軸。
三維拓樸絕緣體的輸運性質與場效電晶體元件研究
最直接能確認三維拓樸絕緣體是否有表面態的實驗的則是使用角分辨光電子能譜 (ARPES),但是ARPES相當昂貴,甚至需要有同步輻射強光源,並不是容易方便量測,所以大部分的實驗室是先簡單透過電子輸運性質的研究來探討表面態。
由於Bi2Se3之EF 較高,會使得體態 (Bulk States) 跟表面態的載子濃度常一起貢獻在電性量測上。解決的方法是透過使用Sb的參雜或外加偏壓來調整費米能階,使得電子在傳輸的時候降低體態的貢獻,提升表面態的貢獻。以下舉兩個例子說明我們的實驗是如何做到的。
Bi2Se3場效電晶體元件
第一個例子,我們將Bi2Se3的拓樸絕緣體薄膜成長在非晶相的二氧化矽/矽晶(SiO2/Si) 的基板上,這樣的基板是半導體業界常用,非常方便製作成控制背閘極 (back gate) 的電晶體 (Field Effect Transistors, FET) 元件,如圖七 (a) 所示。藉由背閘極電壓的控制,可以將載子濃度下降到4 x1012cm-2 (圖七(b)),由於三維拓樸絕緣體的表面態行為,是一種二維電子氣的表現,在低維的介觀物理中,二維電子氣是以e2/h爲單位做量子化的特殊現象表徵,透過磁電導的量測能夠明顯地表現出量子干涉到無序的改變。
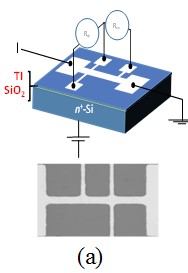

圖七 (a) Bi2Se3薄膜成長在SiO2/Si的場效電晶體元件,(b)藉由背閘極電壓的控制,可以將載子濃度下降到4 x 1012cm-2 。
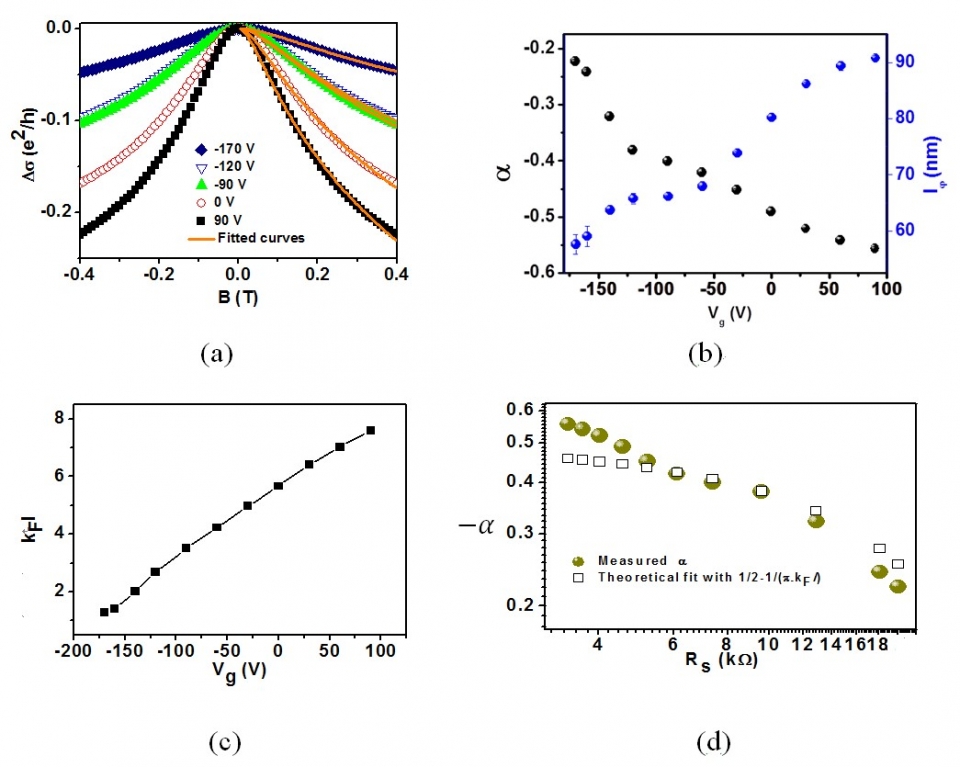
圖八 (a)在Bi2Se3場效電晶體元件的磁電導的量測中,可以觀察到WAL的行為,(b)描述同調性輸運通道特徵的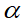 及
及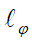 值隨著外加偏壓的變化,(c)
值隨著外加偏壓的變化,(c) 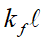 隨施加偏壓的變化,(d) 實驗和理論
隨施加偏壓的變化,(d) 實驗和理論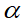 值的擬合
值的擬合
在Bi2Se3場效電晶體 (Field Effect Transistors, FET) 元件的磁電導的量測中,可以觀察到WAL的行為 (圖八(a))。拓樸絕緣體的WAL磁電導行為可以藉由Hikami-Larkin-Nagaoka (HLN) 方程式來描述[17]
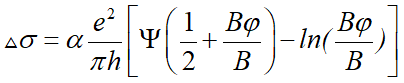 (1)
(1)
我們可以透過公式 (1) 擬合磁電導的行為,觀察表面態的變化。公式 (1) 中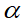 描述表面態數或輸運通道數,當
描述表面態數或輸運通道數,當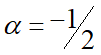 代表電子輸運有一個同調性的輸運通道 (coherent channel),在拓樸絕緣體中有一個表面態; 當
代表電子輸運有一個同調性的輸運通道 (coherent channel),在拓樸絕緣體中有一個表面態; 當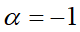 的時候代表電子輸運有二個coherent channel和二個表面態。
的時候代表電子輸運有二個coherent channel和二個表面態。 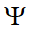 是數學函數中的 digamma 方程[18] ;
是數學函數中的 digamma 方程[18] ; 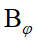 是特徵磁場
是特徵磁場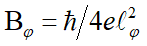 而
而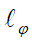 是相位相干特徵長度。
是相位相干特徵長度。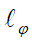 的意義是佔據某一個本徵態的電子,在完全失去相位相干性之前所傳播的平均距離。相位相干長度反映了電子在動力學過程保持相位相干性的最大範圍。通常施加負偏壓 (閘極電壓) Vg會將費米能階EF推往DP 方向移動,當EF越往下移動的時候,體態載子的貢獻越少,表面態載子的貢獻越多,因為比較不容易產生背向散射,所以可以維持相干性行走的更遠,若單單考慮此因素
的意義是佔據某一個本徵態的電子,在完全失去相位相干性之前所傳播的平均距離。相位相干長度反映了電子在動力學過程保持相位相干性的最大範圍。通常施加負偏壓 (閘極電壓) Vg會將費米能階EF推往DP 方向移動,當EF越往下移動的時候,體態載子的貢獻越少,表面態載子的貢獻越多,因為比較不容易產生背向散射,所以可以維持相干性行走的更遠,若單單考慮此因素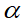 (絕對值) 應該要上升才是,但實驗上卻看到相反趨勢,
(絕對值) 應該要上升才是,但實驗上卻看到相反趨勢,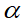 (絕對值) 隨著外加負偏壓卻越下降的趨勢 (圖八(b) )。在討論輸運性質時,還有一重要參數需考量,根據Ioffe-Regel criterion,
(絕對值) 隨著外加負偏壓卻越下降的趨勢 (圖八(b) )。在討論輸運性質時,還有一重要參數需考量,根據Ioffe-Regel criterion,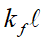 值決定不同輸運機制的極限; kF 是電子在費米能階之波向量值 (可由mobility決定),
值決定不同輸運機制的極限; kF 是電子在費米能階之波向量值 (可由mobility決定), 則是電子之平均自由路徑。當施加偏壓的時候,可以會將系統從
則是電子之平均自由路徑。當施加偏壓的時候,可以會將系統從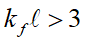 的量子擴散 (quantum diffusive) 範疇,調變到
的量子擴散 (quantum diffusive) 範疇,調變到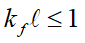 的無序 (disorder) 行為,如圖八(c) 所示。後者之輸運特徵接近一般絕緣體,在此情況下
的無序 (disorder) 行為,如圖八(c) 所示。後者之輸運特徵接近一般絕緣體,在此情況下 需要進行修正。根據Liao 等人在PRL一篇文章[19]提到
需要進行修正。根據Liao 等人在PRL一篇文章[19]提到 的修正公式如下
的修正公式如下
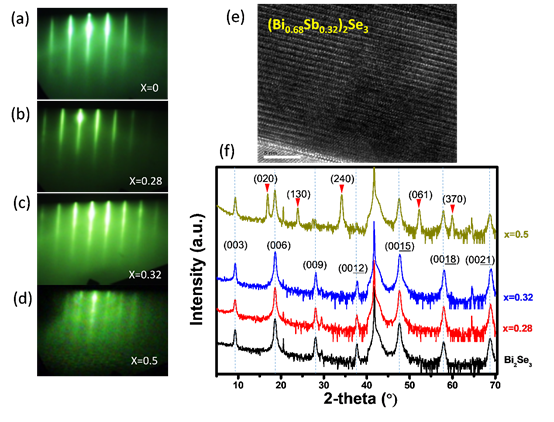
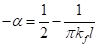 (2)
(2)
(圖八(d)) 可以看到在低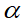 值的情況下擬合的比較好。主要原因有兩個,一是因為Bi2Se3成長在沒有晶相的SiO2基板上,原子排列比較混亂,再者此元件之Bi2Se3薄膜厚度剛好在7nm,介於三維拓樸絕緣體上下表面態耦合的臨界厚度。
值的情況下擬合的比較好。主要原因有兩個,一是因為Bi2Se3成長在沒有晶相的SiO2基板上,原子排列比較混亂,再者此元件之Bi2Se3薄膜厚度剛好在7nm,介於三維拓樸絕緣體上下表面態耦合的臨界厚度。
(Bi1-xSbx)2Se3場效電晶體元件
第二個例子,我們將高品質(Bi1-xSbx)2Se3拓樸絕緣體薄膜成長在三氧化二鋁 (Al2O3)的基板上,透過Sb參雜可以降低母體拓樸絕緣體Bi2Se3的載子濃度; 再藉由改變(Bi1-xSbx)2Se3的厚度則可增加其表面態的貢獻。如此可以達到更大的元件操控範圍。在拓樸絕緣體薄膜成長過程中調整Sb流量,可以得到了不同比例的 (Bi1-xSbx)2Se3拓樸絕緣體薄膜,從圖九中之電子繞射與X光繞射可以看到太高比例的Sb參雜(x > 0.5),會產生非拓樸絕緣體之雜相Sb2Se3的繞射峰。
圖九 30nm (Bi1-xSbx)2Se3的 (a)-(d) 電子繞射與 (f)X光繞射。(e) 原子解析TEM結構
圖十 (a)-(d) 30nm (Bi1-xSbx)2Se3拓樸絕緣體薄膜隨Sb參雜之電性量測
從電性的量測觀察到隨Sb參雜增加到x ~0.3,(Bi1-xSbx)2Se3薄膜之霍爾電阻(Rxy)之非線性部分(圖十(a))及電阻率(Rs或Rxx,圖十(b)) 隨之增加;載子濃度也大幅度的下降約75%(圖十(c));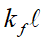 則從降100到10,尚在量子擴散輸運範疇。隨Sb參雜增加到x ~0.3,ARPES的量測 (圖十一) 觀察到 (Bi1-xSbx)2Se3保有良好的表面態,並且費米能階也隨著Sb參雜而明顯降低,與電性量測相當吻合。
則從降100到10,尚在量子擴散輸運範疇。隨Sb參雜增加到x ~0.3,ARPES的量測 (圖十一) 觀察到 (Bi1-xSbx)2Se3保有良好的表面態,並且費米能階也隨著Sb參雜而明顯降低,與電性量測相當吻合。
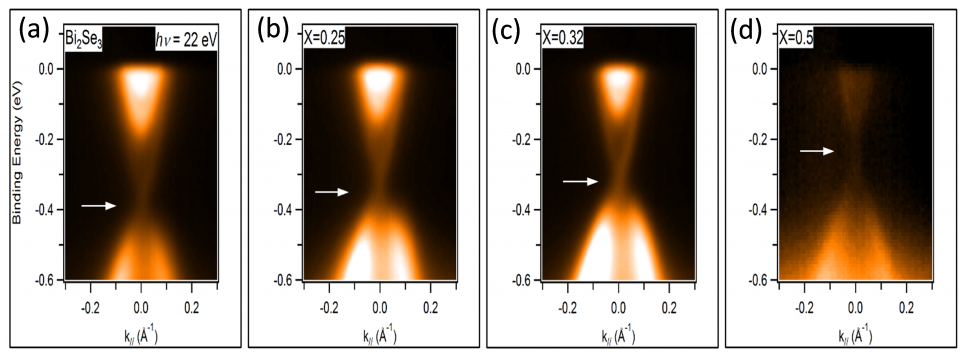
圖十一 (a)-(d) (Bi1-xSbx)2Se3拓樸絕緣體薄膜隨Sb參雜之ARPES量測
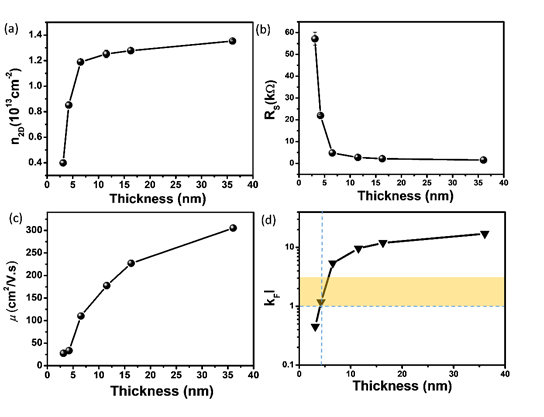
圖十二 (a)-(d) (Bi0.68Sb0.32)2Se3的拓樸絕緣體薄膜隨其厚度變化之電性量測
接著我們挑選比例為 (Bi0.68Sb0.32)2Se3的拓樸絕緣體薄膜改變其厚度作電性量測(圖十二)。隨著厚度減少,(Bi0.68Sb0.32)2Se3之載子濃度更大幅度下降 (圖十二(a)); 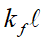 可以從量子擴散 (
可以從量子擴散 (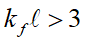 ) 轉變到一般絕緣體 (
) 轉變到一般絕緣體 (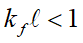 )的行為 (圖十二(d))。最後我們選擇厚度 (~5nm) 和
)的行為 (圖十二(d))。最後我們選擇厚度 (~5nm) 和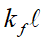 ~3左右的 (Bi0.68Sb0.32)2Se3薄膜,並以用高介電材料SrTiO3基板取代Al2O3做FET場效調控的量測。在電阻率對偏壓的量測我們觀察到一個非常巨大的 (25000%) 的開關比 (On/Off ratio),如圖十三 (a) 所示。然而圖中為什麼會出現多重迴路的現象? 可能的原因是SrTiO3基板表面的氧離子電偶矩所造成的電滯效應,第一次加偏壓時需要較大的電壓去克服氧離子電偶矩帶來的電場,之後就不需要。而為什麼有這麼大的開關比呢?主要是因為拓樸絕緣體在薄膜超薄的情況下,上下表面容易產生耦合,導致表面態會打開會形成一個能隙。當施加偏壓調控費米能階,使之剛好落在表面態會打開能隙中,就會觀測到非常巨大的場效。根據不同厚度的
~3左右的 (Bi0.68Sb0.32)2Se3薄膜,並以用高介電材料SrTiO3基板取代Al2O3做FET場效調控的量測。在電阻率對偏壓的量測我們觀察到一個非常巨大的 (25000%) 的開關比 (On/Off ratio),如圖十三 (a) 所示。然而圖中為什麼會出現多重迴路的現象? 可能的原因是SrTiO3基板表面的氧離子電偶矩所造成的電滯效應,第一次加偏壓時需要較大的電壓去克服氧離子電偶矩帶來的電場,之後就不需要。而為什麼有這麼大的開關比呢?主要是因為拓樸絕緣體在薄膜超薄的情況下,上下表面容易產生耦合,導致表面態會打開會形成一個能隙。當施加偏壓調控費米能階,使之剛好落在表面態會打開能隙中,就會觀測到非常巨大的場效。根據不同厚度的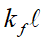 量測,我們可以做出一個厚度改變跟傳輸性質的相圖 (圖十三(b)),在5到12奈米的薄膜厚度區間,是最接近理想元件中的區域,可將從
量測,我們可以做出一個厚度改變跟傳輸性質的相圖 (圖十三(b)),在5到12奈米的薄膜厚度區間,是最接近理想元件中的區域,可將從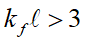 改變至
改變至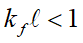 ,亦即輸運特性可從拓樸絕緣體表面態主導轉變到像一般絕緣體的行為,這種改變稱之為拓樸相變 (Topological Phase Transition, TPT)。
,亦即輸運特性可從拓樸絕緣體表面態主導轉變到像一般絕緣體的行為,這種改變稱之為拓樸相變 (Topological Phase Transition, TPT)。
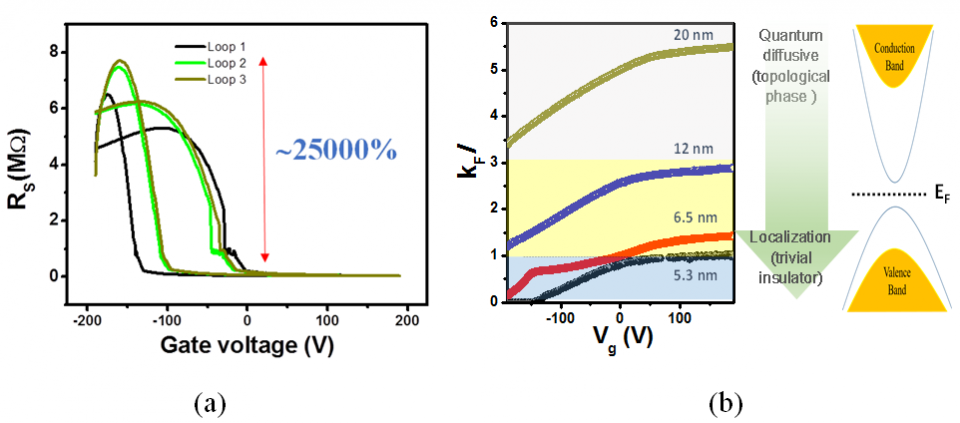
圖十三 5nm (Bi0.68Sb0.32)2Se3的拓樸絕緣體電晶元件 (a) 電阻率和 (b) 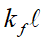 隨施加偏壓的變化
隨施加偏壓的變化
結語
由於拓樸絕緣體之表面態具有時間反演對稱性的保護,電子的動量與自旋維持一定方向鎖定關係 (SML)。所以利用拓樸絕緣體作成場效電晶體元件,除了可以作電子數量的開關,還可以做電子自旋的操控。再者,表面態電子不會與雜質產生背向散射,在低能耗元件(如量子電腦)之應用上可能深具潛力。
圖十四是一個結合拓樸絕緣體和磁性電極之自旋閥 (Spin Valve) 元件的示意圖[20],由於SML,電子的自旋方向跟電流前進方向會形成一個固定的夾角 (90度),藉由外加場可以調控磁性電極的磁化方向,當電子自旋與磁性電極同向或是反向的時候,產生通過或不通過磁性電極的行為,此效應通稱為自旋閥效應。此外,我們可以透過施加偏壓調整拓樸絕緣體從拓樸絕緣體表面態主導轉變到像一般絕緣體的行為,結合自旋閥的原理,偵測電子從自旋有序到無序的改變,這些結果已應用到自旋電晶體 (Spin Transistor) 和許多自旋電子元件。拓樸絕緣體不僅是正被熱烈研究的量子材料,在應用上也是非常值得期待的明日之星!
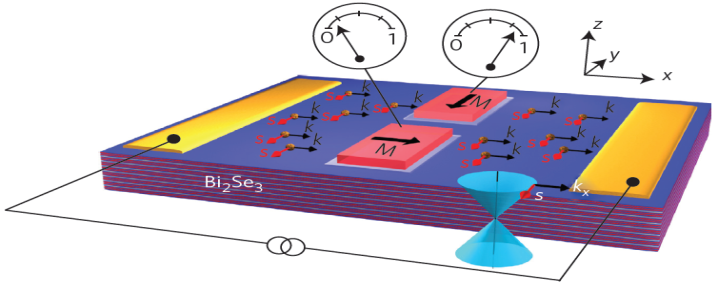
圖十四 結合拓樸絕緣體和磁性電極之自旋閥 (Spin Valve) 元件示意圖[20]
還可以閱讀:拓樸超導體,拓樸材料與拓樸能帶理論,2016年諾貝爾物理學獎:相變與拓樸相變介紹,拓樸物質的理論研究發現,自旋角動量:從愛因斯坦-德哈斯實驗講起,磁性薄膜中之磁矩方向操控
參考論文
- X. L. Qi and S.C.Zhang, phys.today, 63,33 (2010)
- Shuichi Murakami, et al., Science, 301,1348 (2003)
- Jairo Sinova, et al., Phys.Rev.Lett., 92,126603 (2004)
- C. L. Kane, E.J.Mele, Phys.Rev.Lett., 95,226801 (2005)
- B. A. Bernevig, et al., Science, 314, 1757 (2006)
- Markus König, et al., Science, 318, 5851 (2007)
- C. L. Kane, E. J. Mele, Phys.Rev.Lett., 95,146802 (2005)
- L. Fu and C. L. Kane, Phys.Rev.B, 76, 045302 (2007)
- D. Hsieh, et al., Nature, 452, 970 (2008)
- H. Zhang, et al., Nature phys., 5, 438 (2009)
- Y. Xia, et al., Nature phys., 5, 398 (2009)
- D. Hsieh, et al., Phys.Rev.Lett., 103, 146401 (2009)
- Q. L. He, et al., Science, 357, 6348 (2017)
- X. L. Qi and S. C. Zhang, Physics Today, 63 (1), 33 (2010)
- Charles Day, Physics Today, 61(1), 19 (2008)
- Z. G. Chen, et al., Natural Science, 22(6), 535-549 (2012)
- S. Hikami, A. I. Larkin, Y. Nagaoka, "Spin–Orbit Interaction and Magnetoresistance in the Two-Dimensional Random System", Progress of Theoretical Physics. 63 (2) , 707–710 (1980)
- The digamma function is defined as the logarithmic derivative of the gamma function. See "Handbook of Mathematical Functions and Formula, Graphs, and mathematical Tables" (10th ed.). New York: Dover. pp. 258–259. (1972)
- J. Liao, et al. Phys. Rev. Lett. 114, 21660 (2015).
- C. H. Li, et al. Nat Nanotechnol. 9, 218 (2014)