
描繪質子內部立體風景的部分子物理
- 物理專文
- 撰文者:高崇文
- 發文日期:2020-12-16
- 點閱次數:1460
質子在101年前被發現時,與電子一樣被當作是構成世界的惟“二”的基本粒子。雖然在1930年代,科學家透過測量質子的磁偶矩,發現質子的g值並非狄拉克方程式所預測的值以後,才知道質子並非“基本粒子”,而是由更小的粒子所組成,但由於質子的體積極小,實在難以探究其內在的結構。直到五零年代末,美國物理學家羅伯特·霍夫施塔特(英語:Robert Hofstadter,1915年2月5日-1990年11月17日)才藉由電子-質子的彈性碰撞測量出質子的電磁形狀因子 (electromagnetic form factors)。這代表質子內的電荷有著特定的分佈。事實上,就算質子與電子都沒有被極化,利用神奇的Rosenbluth分離公式,科學家還是能是擷取出電的形狀因子與磁的形狀因子。這些決定形狀因子的變數是電子在碰撞前後的四動量的差的平方,這個變數通常寫作Q2,只要知道電子入射的能量與質子與電子的散射角就可以決定出Q2。這等於是給質子畫一個地圖,描繪它內部的電荷與磁矩的分佈。這些資訊雖然肯定了質子內部的確擁有複雜的結構,但是卻沒有透露形成這些結構的組成粒子的任何訊息。
真正揭露質子內部神秘面紗的實驗,是在六零年代末在史丹佛大學的直線加速器(Stanford Linear Accelerator Center, 簡稱SLAC)進行的質子-電子的深度非彈性碰撞(Deep Inelastic Scattering,簡稱DIS)。所謂的深度,是指Q2 值很高,而非彈性則是指碰撞前後的動能不守恒,實際上,由於巨大的動量從電子傳到質子,在碰撞後質子幾乎都被撞碎了。
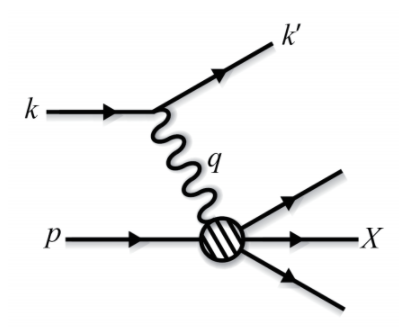
DIS奇特的實驗結果一開始讓物理學家感到十分困惑,然而很快地,大物理學家費恩曼 (Richard Feynman) 提出一個絕妙的解答,只要把電子與質子的DIS看成是眾多獨立的電子與質子中帶有電荷的基本粒子的彈性碰撞,具體地講,就是電子與質子的DIS的散射截面在Bjorken極限時會等於是質子與組成質子的點狀粒子的散射截面的和。這樣Bjorken的觀察就可以說得通了!
通常一個複合粒子參與一個物理過程,假設只有一個組成粒子牽扯在碰撞過程中,那應該是將各個組成粒子的散射振幅加起來再平方得到散射截面,可是在DIS這裡卻是將各別的射振幅平方後再相加。更神奇的是這個新的變數x = Q2 / 2Mν,0 ≦ x ≦ 1,居然等於這個點狀粒子帶的動量與原先初態的質子動量的比。不過要注意的是這個結論是在無限動量座標系 (infinite momentum frame, IMF) 才會成立的。這說明了結構函數只會是x的函數。
這個點狀粒子則被費恩曼稱為部分子 (parton),一開始這個模型就被稱為是部分子模型 (parton model)。在這個模型中,結構函數只會有一個是獨立的,而且它的意義是帶著動量為原始質子動量的x的部分子與光子作用的機率。這個函數被稱為“部分子分佈函數”(Parton Distribution Functions, 簡稱 PDFs)。的確,在高Q2與ν值的運動條件下,兩個結構函數F1、F2果然滿足一個稱為Callan-Cross關係,所以原則上在Bjorken極限時DIS的散射截面可以擷取出質子中的組成粒子的PDF。於是乎,質子電子的DIS打開了一扇門,讓物理學家得以一探構成質子的組成粒子的相關資訊。
然而部分子模型有一點叫人不解,就是部分子彼此之間是沒有交互作用的! 那等於說質子是一束自由的帶電基本粒子。但是自由的點狀粒子如何能形成一個像質子如此緊緻的物體呢?而且從質子的靜止座標系來看,明明是一個自旋二分之一,質量是938 MeV,帶有特定磁矩的的粒子。明明是同一個物體,怎麼在兩個座標系看,卻有著天淵之別呀? 這些難題要等到1973年理論物理學家發現了所謂“漸進自由”(asymptotic freedom) 才逐漸得到解答。要說明這件事,只能從頭說起了…
其實早在DIS實驗之前,就有物理學家懷疑質子是由自旋為二分之一的基本粒子所組成。六零年代初,物理學家Murray Gell-Mann就從性質類似的重子與介子的性質下手,運用數學的群論,歸納出夸克模型 (Quark Model)。在夸克模型中質子是由兩個u夸克(帶+2/3個基本電荷)與一個d夸克(帶-1/3個基本電荷)所組成。但是實驗室從來沒有發現帶著+2/3或-1/3個基本電荷的粒子,所以許多人對夸克的真實性存疑,直到DIS的實驗以及費恩曼的部分子模型之後,科學界才慢慢地接受夸克。至於夸克透過何種交互作用而形成質子呢?答案卻藏在夸克模型中。
科學家在研究夸克模型曾經踢到一塊鐵板,就是核子共振態Δ++ (1232)。這個共振態的自旋是3/2,夸克模型中這個共振態的波函數必定是對稱的,因為它只能是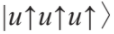 ,但是自旋統計定理告訴我們,自旋是半整數的粒子的波函數,必需是反對稱的。所以韓國的物理學家韓武榮與日本的物理學家南部陽一郎就以此假設,夸克還帶有隱藏的自由度,由此建構出對稱群為SU(3) 的規範場論,這個理論中,夸克透過交換無質量且自旋為一的規範玻色子,膠子 (gluon),來彼此作用,就如同電子之間交換光子一般。由於SU(3) 是不可交換群,所以膠子彼此也會交互膠子來作用。這就是強作用力的基本理論:量子色動力學(Quantum Chromodynamics,簡稱QCD)。但是膠子雖然帶有SU(3) 理論中的色荷,卻不帶電荷,不會與光子作用,所以在質子-電子的DIS是無法直接測量的到。
,但是自旋統計定理告訴我們,自旋是半整數的粒子的波函數,必需是反對稱的。所以韓國的物理學家韓武榮與日本的物理學家南部陽一郎就以此假設,夸克還帶有隱藏的自由度,由此建構出對稱群為SU(3) 的規範場論,這個理論中,夸克透過交換無質量且自旋為一的規範玻色子,膠子 (gluon),來彼此作用,就如同電子之間交換光子一般。由於SU(3) 是不可交換群,所以膠子彼此也會交互膠子來作用。這就是強作用力的基本理論:量子色動力學(Quantum Chromodynamics,簡稱QCD)。但是膠子雖然帶有SU(3) 理論中的色荷,卻不帶電荷,不會與光子作用,所以在質子-電子的DIS是無法直接測量的到。
那麼量子色動力學如何解釋質子在深度非彈性碰撞與低Q2值的彈性碰撞中表現出來截然不同的樣貌呢?這是因為在規範場論中,耦合係數ɑs其實是隨著交換的規範玻色子四動量平方而改變。在量子電動力學中,耦合係數隨著交換動量平方增加而增加,但是David Gross、David Politzer和Frank Wilczek卻發現量子色動力學中的耦合常數(只要夸克種類不多於16種)隨著交換動量平方增加而減少,這就完美地解釋了為何質子在靜止座標係是個緊緻的束縛態,到了無限動量座標系卻像是一叢自由粒子。因為在無限動量座標系夸克交換膠子的動量平方都很大,而在靜止座標夸克交換膠子的動量平方都很小,所以在前者夸克幾乎是自由的,在後者耦合係數則變成很大。這就是有名的“漸進自由”。
有了QCD,照理說,質子的一切性質都可以利用這個基本理論來計算才對。可惜的是,不要說質子的形狀因子我們算不出來,就連質子的質量這麼基本的物理量,也無法用QCD來計算。因為當偶合係數大於一的時候,傳統使用的微擾展開就失效。這與量子電動力學的成功成了鮮明的對比。那麼深度非彈性碰撞散射的主角,部分子分佈函數 (PDFs) 能不能用QCD來算呢?殘念,答案依然是不行!理由在後頭我再詳述。然而QCD倒是可以算出PDFs怎麼隨著Q2改變。這個方程式叫DGLAP方程式,分別用了五位作者的頭文字 (Dokshitzer–Gribov–Lipatov–Altarelli–Parisi)。在Bjorken 極限時PDF 的確與Q2 無關,然而實驗總是在有限的Q2的條件下作的,得到的結果當然還是隨著Q2值改變而改變。科學家只能用DIS實驗的結果來擷取結構函數,再從結構函數中擷取質子中夸克的PDF,而DGLAP 方程式則幫助物理學家們將在不同Q2值得到的實驗數據統合在一起,得到精準的PDFs。
這事說來容易,做起來可不簡單。因為在DIS中,所有夸克的貢獻都加在一起,怎麼將u夸克與d夸克的PDF分別出來?這只能仰賴中子的DIS實驗,但是自由中子會衰變,所以只能用氘核的DIS。更進一步,在質子中u夸克與d夸克能發射出膠子,膠子能放出夸克-反夸克對,所以質子中有膠子與反u夸克、反d夸克,還有s夸克、反s夸克,甚至還可能有微量的c夸克與反c夸克。所以除了電子-質子(氘核)DIS之外,微中子-質子(氘核)DIS 也要派上用場。微中子與質子交換的不是光子,(因為微中子不帶電),而是交換得是弱作用的媒介,W與Z玻色子。s夸克雖然與d夸克的電荷相同,但是與W與Z玻色子的耦核係數不同,這就讓科學家區分s夸克與d夸克的PDF。膠子不跟光子,也不跟W與Z玻色子發生作用,它的PDF只能從不同Q2值得到的實驗數據中去擷取,因為它出現在DGLAP 方程式中。或是利用所謂的Drell-Yan 過程來擷取。所謂Drell-Yan 過程是利用兩個強子的非彈性碰撞而在末態產生輕子對,在特定的運動條件下,這個過程可以視為強子的部分子(夸克與反夸克)相互湮滅成光子或是Z玻色子再對生輕子對。DIS與Drell-Yan 過程所擷取的PDF 理當是相同的物理量,這是部分子物理的一大挑戰。
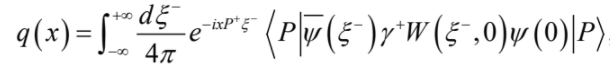
在此, ξ -=ξ0 -ξ3/21/2 , ξ+=ξ0+ξ3 /21/2 。非局所算子之所以是非局所乃是因為它定義在兩點之間 (0,ξ),而且ξ+=ξ1=ξ2=0。換句話說這個算子是定義在光錐上的兩個點,兩點之間完全沒有橫向的距離。為了讓這個算子保持規範不變性,還要再加上定義如下W(ξ-,0)
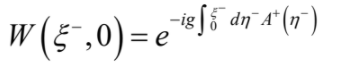
A 代表的是膠子場。這是所謂的Wilson Line。它代表的是帶著xp動量的部分子與質子的其他部份交換低動量平方的膠子的效應。一般我們會選擇光錐規範條件:A+ = 0,這樣Wilson Line 等於1就可以不必理會它了。不過在更一般的情況,就沒辦法不管它了。後頭我們會再討論它的。
雖然PDF的研究已經持續了超過半世紀,不管是理論,還是實驗都累積了許多成果,然而所得到的基本上都只有縱向的資訊。至於橫向的資訊則是一片空白。但是若想要想擴展部分子的知識到橫向,卻比想像中困難多了。不只是實驗更加困難,就是在理論層面上也要複雜許多。這是由於在無窮動量座標系中,只有一個相關的能量規模,就是質子的動量p,所有的量都是以它為基準,這簡化了整個分析。但是一旦將橫向的分布放進考慮,等於引進了第二個的能量規模,這讓整個分析起了巨大的變化。此外還有一個重要的因素,就是夸克,膠子都是擁有自旋的基本粒子,所以就算我們不考慮部分子的橫向動量與位置,僅僅讓部分子的自旋指向與其動量垂直的方向,就會浮現新的困難。舉例來講,DIS即使在扭度展開的首階,也有三個不同的PDF,可以圖示如下
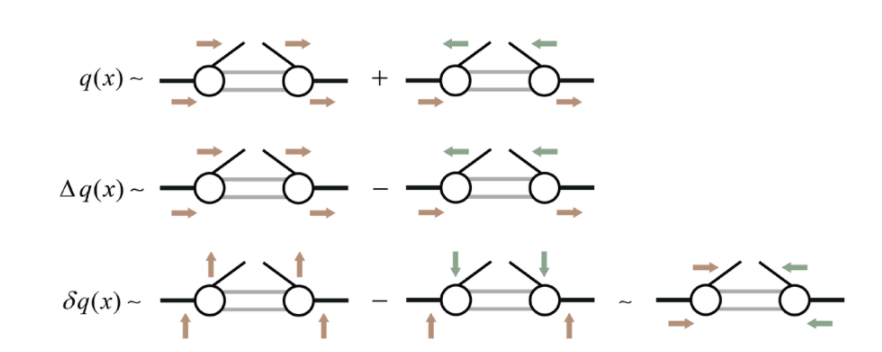
圖四:扭度展開首階的三種PDF
紅色橫向的箭頭代表自旋與其動量平行(helicity 為正),綠色代表反平行(helicity為負),上下的箭頭代表的是自旋與動量垂直。橫向自旋的本徵態是縱向自旋的本徵態的線性疊加。第一種是我們之前談論的PDF。第二種PDF稱之為極化部分子分佈,第三種PDF稱之為橫向部分子分佈(Transversity parton distribution function)。極化部分子分佈可以藉由縱向極化的電子與質子的DIS來測量,然而橫向部分子分佈卻無法由DIS來擷取,因為光子的作用不會改變粒子的helicity,只有部分子的質量能改變helicity。但是u、d夸克的質量非常小,所以要量到這個PDF,只能藉由被極化的質子的Drell-Yan過程,或是讓末態的部分子透過強子化(hadronization)來改變helicity了。這讓橫向部分子分佈的擷取幾乎成了mission impossible!

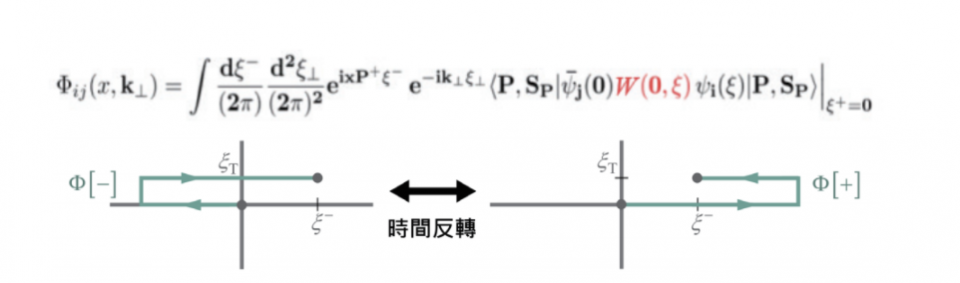
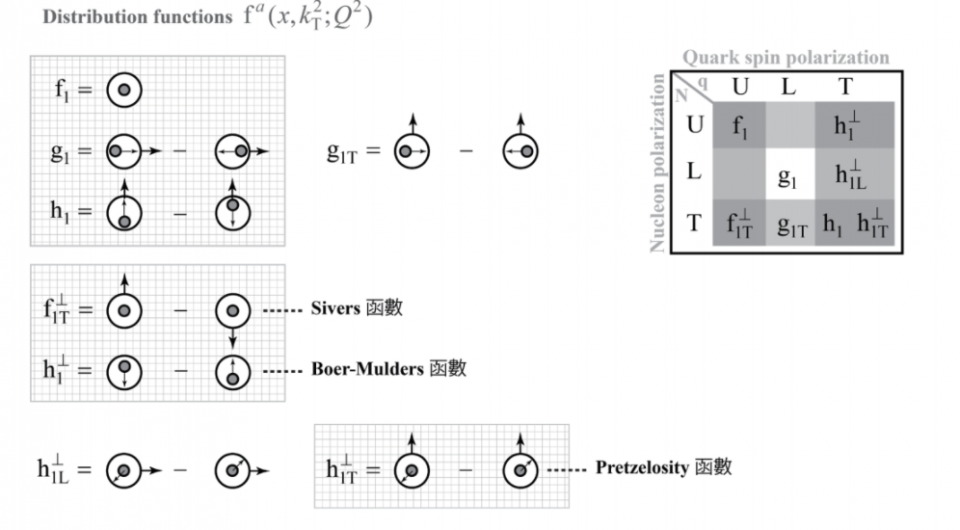
依照質子與夸克的自旋指向,我們可以得到在扭度展開下的首階有八個TMD-PDFs。 f1,g1與h1這三個函數對部分子橫向動量kT積分以後就是原先的三種PDFs。此外還有五個新的函數,如果對對部分子橫向動量積分以後會得到零。其中受到最多注目的是Sivers 函數 f1T。這是橫向極化的質子的非極化夸克分佈。它之所以受到注目是因為它是naive T-odd。也就是說,乍看之下,在實行時間反轉的變換後,Sivers 函數會多出一個負號,既然QCD是時間反轉不變的理論,那麼Sivers 函數就該為零才對,但是這個推論忽略了一點,就是Wilson Line。先前我們提過,若是採用光錐規範Wilson Line的值為1,但是如果是連接Wilson Line的兩點有橫向位移的話,這個結論就不成立了,因為光錐規範無法完全決定膠子場,考慮Wilson Line的標準途徑,Wilson Line 會變成複數,在考慮時間反轉時,物理量要取複數共軛, Wilson Line提供的相位就使得Sivers 函數不為零也不會違反時間反轉不變性。除了Sivers 函數以外,Boer-Mulders 函數h1也是naive T-odd。基於相同原因,也不會因時間反轉不變性而被排除。Boer-Mulders 函數是非極化質子中橫向極化部分子的分佈,與Sivers函數恰恰相反。
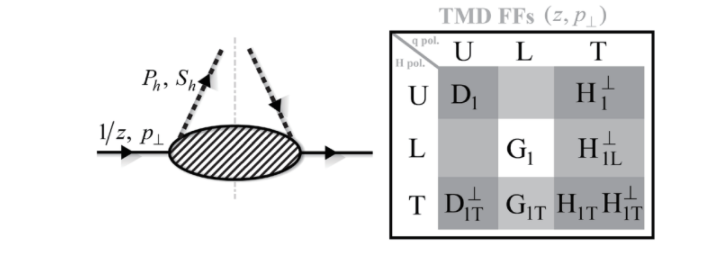
這麼多未知的TMD-PDFs,要從哪些實驗數據來擷取它們呢? 主要是從兩種實驗來下手。一種是極化的質子的Drell-Yan 過程,另外一個實驗就是所謂的半包容性深度非彈性碰撞(semi-inclusive Deep inelastic scattering, 簡稱SIDIS)。前者的困難在於散射截面很小,測量不易。而且不同種類的夸克的貢獻加總在一起。後者的難處則在於散射截面是TMDPDFs 與 TMDFFs (Transverse momentum dependent fragmentation functions)的捲積(convolution)。所謂碎形函數 (fragmentation functions) 指的是動量為P的夸克放出動量為zP的強子的機率。一般是從正負電子湮滅成虛光子再對生正負夸克對,夸克與反夸克放出強子的過程來反推碎形函數。不意外的, TMDFFs 也有八種。其中最重要的,除了非極化的TMPFF,D1之外就屬科林斯 (Collins) 函數H1了。這是由於即使用非極化的電子與質子,散射截面中還是有一項是Boer-Mulders 函數h1與科林斯函數H1的捲積。
如果將質子橫向極化的話,可以由不同極化方向結果的差來擷取Sivers函數與D1捲積;Transversity 函數與科林斯函數H1的捲積,以及Pretzelosity 函數 h1T的捲積。第一個組合隨著sin(ϕh-ϕs),第二個組合隨著sin(ϕh+ϕs),第三個組合隨著sin(3ϕh-ϕs)。縱向極化的質子則能提供h1L與科林斯函數的捲積。若是同時讓電子與質子都極化的話,可以得到g1與g1T與D1的捲積。
至於Drell-Yan 過程中可以藉由質子極化方向來擷取Boer-Mulders 函數,Siversc 函數,Transversity 以及Pretzelosity 函數。從Drell-Yan 過程的結果來擷取的好處是不需要擁有任何碎形函數的知識。但是由於Wilson Line 的路徑與SIDIS不同的關係,物理學家預測由Drell-Yan 過程得到的Siversc 函數與從SIDIS得到的,會存在著一個負號的差異! 這個預測正初步與實驗結果吻合,但是仍需要更精確的實驗數據來支持。TMDPDF 如何隨Q2 演化是個理論難題,甚至將SIDIS的實驗條件並不是如DIS那樣容易判斷是否能採用“手提袋近似”,放出強子的夸克也未必是被虛光子打到的部分子,這都是TMDPDF 研究遇到的障礙,這些專門的問題,這裡就不多說了。
雖然有五花八門的TMD-PDFs, 但是這些卻沒有辦法告訴我們部分子在橫向位置上的分佈。所以我們需要從別的物理量來探索這方面的訊息。這個物理量稱之為廣義部分子分佈(Generalized Parton Distributions, 簡稱為GPD)。這個物理量是這樣定義的
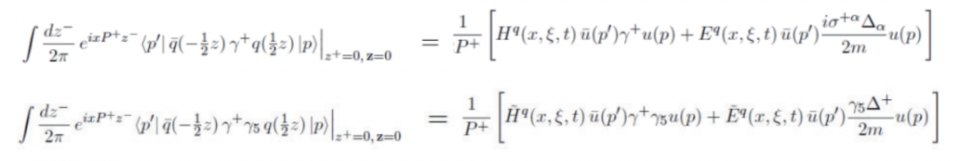
圖十一:GPD示意圖
GPDs 有許多神奇的性質。首先GPD提供了一個連接形狀因子與PDF的橋樑。當Δ=0, GPD 自然回到PDF。這個稱為forward limit。另一方面,如果我們講GPD對x作積分,從-1積到1,將會得到如下的結果:
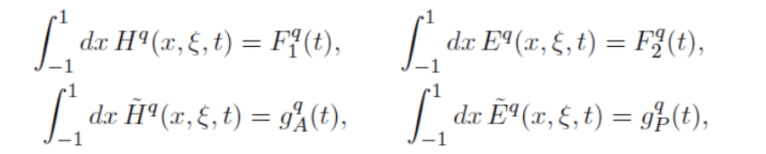
圖十二:形狀因子與 GPD 的關係。
F1(t) 是所謂的Dirac form factor,F(t) 是Pauli form factor,而電的形狀因子是GE(t) = F1(t) - τF2(t),τ = Q2/4M2, 磁的形狀因子則是GM(t) = F1(t) + F2(t)。
GPD另外一個神奇的性質是H(t = 0) 與E(t = 0) 的和的二次矩居然等於部分子的總角動量! 事實上,部分子如何組合成一個自旋為二分之一的質子一直是強子物理界的一個大謎題。因為質子的自旋照理說是夸克的自旋角動量加上夸克的軌道角動量再加上膠子的總角動量,因為規範玻色子的角動量雖然可以分成自旋角動量與軌道角動量,但是這個區分是無法維持規範不變性的。從實驗中得知夸克的自旋角動量只貢獻了約莫百分之三十的質子自旋。所以膠子與夸克的GPD成了許多研究的焦點。此外,如果在ξ = 0,對初態與末態橫向動量差作傅利葉變換的話,就得到了部分子在橫向位置b 如何分佈的資訊了:
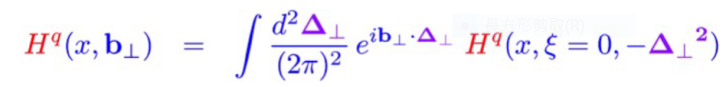
GPD的Q2演化比起TMDPDF單純多了,而判斷實驗條件是否符合手提袋近似也比TMDPDF來得容易,問題是擁有這些神奇性質的物理量GPD好不好量呢? 答案是非常困難。估且不論GPD本身是三個變數的函數,光是必須從排斥性過程的實驗來擷取就讓整個擷取過程變得比PDF困難多了。最常見的是從深度康普頓散射(Deep Virtual Compton Scattering, 簡稱 DVCS)的實驗結果來處理。DVCS是電子與質子交換一個動量平方很高的光子,然後質子釋放一個光子的散射過程。另外一個可能的實驗室光致介子生成(Hard Exclusive Meson Production)。
利用DVCS的難處在於大部分的散射截面都是Bethe-Heitler (BH) 過程,即末態的光子從電子發出,而非從質子放出。所以科學家必須從BH過程與DVCS過程的干涉項來擷取GPD。另外一個問題是在DVCS中,個種夸克的貢獻都加總在一起。 從HEMP擷取GPD的問題則是散射截面與GPD的乘積有關,但在DVCS則是GPD與質子形狀因子的乘積。此外要從HEMP擷取GPD 還需要知道屆子的distribution amplitude(簡稱DA), 這又帶來新的麻煩。科學家努力擷取GPD也超過了二十年了,成果卻還遠遠部如PDF的豐碩,實在是個相當艱難的任務。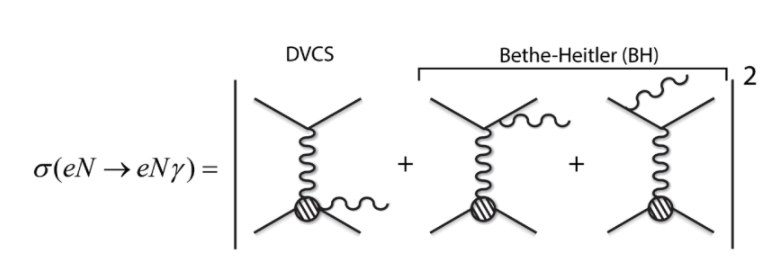
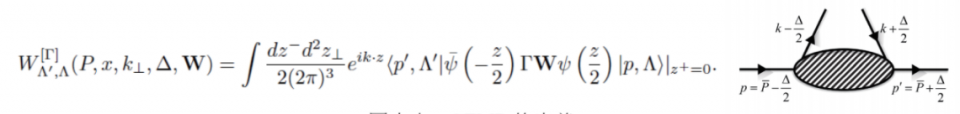
作者:高崇文 教授中原大學物理系
真正揭露質子內部神秘面紗的實驗,是在六零年代末在史丹佛大學的直線加速器(Stanford Linear Accelerator Center, 簡稱SLAC)進行的質子-電子的深度非彈性碰撞(Deep Inelastic Scattering,簡稱DIS)。所謂的深度,是指Q2 值很高,而非彈性則是指碰撞前後的動能不守恒,實際上,由於巨大的動量從電子傳到質子,在碰撞後質子幾乎都被撞碎了。

圖一:DIS示意圖
很難想像這樣的實驗居然會提供任何有用的資訊,但是非常幸運的是SLAC的理論物理學家James D Bjorken觀察到一件重要的事實:原本電子-質子DIS的散射截面決定於兩個結構函數 (structure functions),這兩個結構函數原本應該是這兩個變數:ν,電子碰撞前後的能量差(在靶為靜止的實驗座標系測量)與Q2的函數,但是在Q2很高的情況下,結構函數卻似乎逐漸與Q2無關!James D Bjorken Q2提出一個假設,假設Q2與ν都趨向無窮大,但是兩者比值固定,換言之,如果採用新的變數x = Q2 / 2Mν,0 ≦ x ≦ 1,那麼兩個結構函數F1與F2都只是x的函數。這個極限被稱為Bjorken 極限。DIS奇特的實驗結果一開始讓物理學家感到十分困惑,然而很快地,大物理學家費恩曼 (Richard Feynman) 提出一個絕妙的解答,只要把電子與質子的DIS看成是眾多獨立的電子與質子中帶有電荷的基本粒子的彈性碰撞,具體地講,就是電子與質子的DIS的散射截面在Bjorken極限時會等於是質子與組成質子的點狀粒子的散射截面的和。這樣Bjorken的觀察就可以說得通了!
通常一個複合粒子參與一個物理過程,假設只有一個組成粒子牽扯在碰撞過程中,那應該是將各個組成粒子的散射振幅加起來再平方得到散射截面,可是在DIS這裡卻是將各別的射振幅平方後再相加。更神奇的是這個新的變數x = Q2 / 2Mν,0 ≦ x ≦ 1,居然等於這個點狀粒子帶的動量與原先初態的質子動量的比。不過要注意的是這個結論是在無限動量座標系 (infinite momentum frame, IMF) 才會成立的。這說明了結構函數只會是x的函數。
這個點狀粒子則被費恩曼稱為部分子 (parton),一開始這個模型就被稱為是部分子模型 (parton model)。在這個模型中,結構函數只會有一個是獨立的,而且它的意義是帶著動量為原始質子動量的x的部分子與光子作用的機率。這個函數被稱為“部分子分佈函數”(Parton Distribution Functions, 簡稱 PDFs)。的確,在高Q2與ν值的運動條件下,兩個結構函數F1、F2果然滿足一個稱為Callan-Cross關係,所以原則上在Bjorken極限時DIS的散射截面可以擷取出質子中的組成粒子的PDF。於是乎,質子電子的DIS打開了一扇門,讓物理學家得以一探構成質子的組成粒子的相關資訊。
然而部分子模型有一點叫人不解,就是部分子彼此之間是沒有交互作用的! 那等於說質子是一束自由的帶電基本粒子。但是自由的點狀粒子如何能形成一個像質子如此緊緻的物體呢?而且從質子的靜止座標系來看,明明是一個自旋二分之一,質量是938 MeV,帶有特定磁矩的的粒子。明明是同一個物體,怎麼在兩個座標系看,卻有著天淵之別呀? 這些難題要等到1973年理論物理學家發現了所謂“漸進自由”(asymptotic freedom) 才逐漸得到解答。要說明這件事,只能從頭說起了…
其實早在DIS實驗之前,就有物理學家懷疑質子是由自旋為二分之一的基本粒子所組成。六零年代初,物理學家Murray Gell-Mann就從性質類似的重子與介子的性質下手,運用數學的群論,歸納出夸克模型 (Quark Model)。在夸克模型中質子是由兩個u夸克(帶+2/3個基本電荷)與一個d夸克(帶-1/3個基本電荷)所組成。但是實驗室從來沒有發現帶著+2/3或-1/3個基本電荷的粒子,所以許多人對夸克的真實性存疑,直到DIS的實驗以及費恩曼的部分子模型之後,科學界才慢慢地接受夸克。至於夸克透過何種交互作用而形成質子呢?答案卻藏在夸克模型中。
科學家在研究夸克模型曾經踢到一塊鐵板,就是核子共振態Δ++ (1232)。這個共振態的自旋是3/2,夸克模型中這個共振態的波函數必定是對稱的,因為它只能是
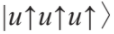 ,但是自旋統計定理告訴我們,自旋是半整數的粒子的波函數,必需是反對稱的。所以韓國的物理學家韓武榮與日本的物理學家南部陽一郎就以此假設,夸克還帶有隱藏的自由度,由此建構出對稱群為SU(3) 的規範場論,這個理論中,夸克透過交換無質量且自旋為一的規範玻色子,膠子 (gluon),來彼此作用,就如同電子之間交換光子一般。由於SU(3) 是不可交換群,所以膠子彼此也會交互膠子來作用。這就是強作用力的基本理論:量子色動力學(Quantum Chromodynamics,簡稱QCD)。但是膠子雖然帶有SU(3) 理論中的色荷,卻不帶電荷,不會與光子作用,所以在質子-電子的DIS是無法直接測量的到。
,但是自旋統計定理告訴我們,自旋是半整數的粒子的波函數,必需是反對稱的。所以韓國的物理學家韓武榮與日本的物理學家南部陽一郎就以此假設,夸克還帶有隱藏的自由度,由此建構出對稱群為SU(3) 的規範場論,這個理論中,夸克透過交換無質量且自旋為一的規範玻色子,膠子 (gluon),來彼此作用,就如同電子之間交換光子一般。由於SU(3) 是不可交換群,所以膠子彼此也會交互膠子來作用。這就是強作用力的基本理論:量子色動力學(Quantum Chromodynamics,簡稱QCD)。但是膠子雖然帶有SU(3) 理論中的色荷,卻不帶電荷,不會與光子作用,所以在質子-電子的DIS是無法直接測量的到。那麼量子色動力學如何解釋質子在深度非彈性碰撞與低Q2值的彈性碰撞中表現出來截然不同的樣貌呢?這是因為在規範場論中,耦合係數ɑs其實是隨著交換的規範玻色子四動量平方而改變。在量子電動力學中,耦合係數隨著交換動量平方增加而增加,但是David Gross、David Politzer和Frank Wilczek卻發現量子色動力學中的耦合常數(只要夸克種類不多於16種)隨著交換動量平方增加而減少,這就完美地解釋了為何質子在靜止座標係是個緊緻的束縛態,到了無限動量座標系卻像是一叢自由粒子。因為在無限動量座標系夸克交換膠子的動量平方都很大,而在靜止座標夸克交換膠子的動量平方都很小,所以在前者夸克幾乎是自由的,在後者耦合係數則變成很大。這就是有名的“漸進自由”。
有了QCD,照理說,質子的一切性質都可以利用這個基本理論來計算才對。可惜的是,不要說質子的形狀因子我們算不出來,就連質子的質量這麼基本的物理量,也無法用QCD來計算。因為當偶合係數大於一的時候,傳統使用的微擾展開就失效。這與量子電動力學的成功成了鮮明的對比。那麼深度非彈性碰撞散射的主角,部分子分佈函數 (PDFs) 能不能用QCD來算呢?殘念,答案依然是不行!理由在後頭我再詳述。然而QCD倒是可以算出PDFs怎麼隨著Q2改變。這個方程式叫DGLAP方程式,分別用了五位作者的頭文字 (Dokshitzer–Gribov–Lipatov–Altarelli–Parisi)。在Bjorken 極限時PDF 的確與Q2 無關,然而實驗總是在有限的Q2的條件下作的,得到的結果當然還是隨著Q2值改變而改變。科學家只能用DIS實驗的結果來擷取結構函數,再從結構函數中擷取質子中夸克的PDF,而DGLAP 方程式則幫助物理學家們將在不同Q2值得到的實驗數據統合在一起,得到精準的PDFs。
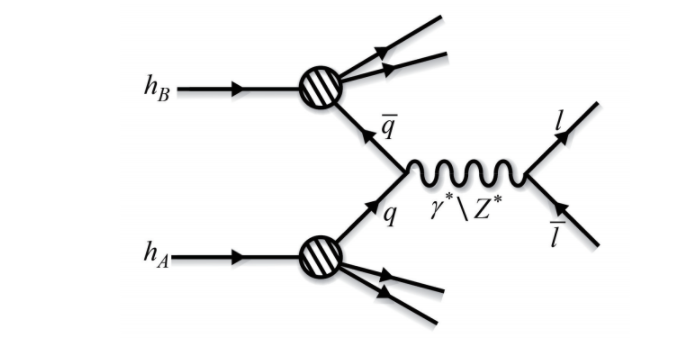
這事說來容易,做起來可不簡單。因為在DIS中,所有夸克的貢獻都加在一起,怎麼將u夸克與d夸克的PDF分別出來?這只能仰賴中子的DIS實驗,但是自由中子會衰變,所以只能用氘核的DIS。更進一步,在質子中u夸克與d夸克能發射出膠子,膠子能放出夸克-反夸克對,所以質子中有膠子與反u夸克、反d夸克,還有s夸克、反s夸克,甚至還可能有微量的c夸克與反c夸克。所以除了電子-質子(氘核)DIS之外,微中子-質子(氘核)DIS 也要派上用場。微中子與質子交換的不是光子,(因為微中子不帶電),而是交換得是弱作用的媒介,W與Z玻色子。s夸克雖然與d夸克的電荷相同,但是與W與Z玻色子的耦核係數不同,這就讓科學家區分s夸克與d夸克的PDF。膠子不跟光子,也不跟W與Z玻色子發生作用,它的PDF只能從不同Q2值得到的實驗數據中去擷取,因為它出現在DGLAP 方程式中。或是利用所謂的Drell-Yan 過程來擷取。所謂Drell-Yan 過程是利用兩個強子的非彈性碰撞而在末態產生輕子對,在特定的運動條件下,這個過程可以視為強子的部分子(夸克與反夸克)相互湮滅成光子或是Z玻色子再對生輕子對。DIS與Drell-Yan 過程所擷取的PDF 理當是相同的物理量,這是部分子物理的一大挑戰。

圖二:Drell-Yan 過程示意圖
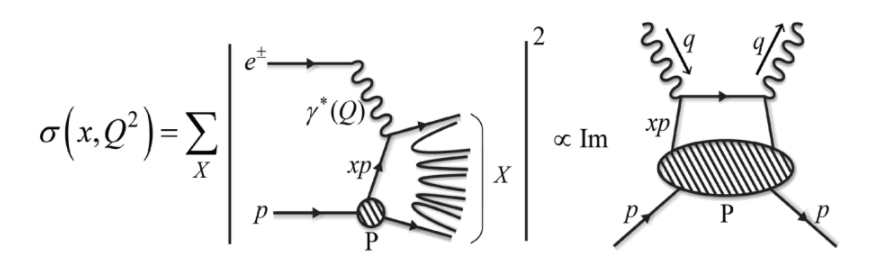
用心的讀者一定會追問,為什麼PDF不能直接用QCD來算呢?首先由於光子的動量很大,所以只能與一個部分子作用,這個近似稱為“手提袋近似”(handbag approximation)。在量子理論的架構下,DIS 的散射截面,在手提袋近似下,可以寫成散射角為零的康普頓散射的振幅的虛部(如圖),而這個振幅分成兩部分,光子與部分子發生作用的部分,還有底下標示著“P”的部分。第二個部分代表的是從質子(動量為p)中“拿”出一個動量為xp的部分子再放回去的機率。光子與部分子交互作用的部分是可以用QCD計算的部分,然而標示著“P”的部分卻是無法用微擾展開來計算的。
圖三:DIS散射截面與康普頓散射
更具體一點地說,這個部分可以寫成兩個代表“流”(current) 的乘積的矩陣元素。利用量子場論的算子乘積展開(Operator Product Expansion,簡稱OPE)可以展開得到隨著(1/ Q2 )n 的各項。這個展開稱之為扭度展開(Twist-expansion)。當Q2 趨近於無窮時,只有展開的首項 (n=0) 能夠存留,對應到結構函數,就可以發現PDF可以寫成是一個非局所 (non-local) 算子的矩陣元素如下: 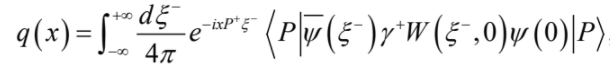
在此, ξ -=ξ0 -ξ3/21/2 , ξ+=ξ0+ξ3 /21/2 。非局所算子之所以是非局所乃是因為它定義在兩點之間 (0,ξ),而且ξ+=ξ1=ξ2=0。換句話說這個算子是定義在光錐上的兩個點,兩點之間完全沒有橫向的距離。為了讓這個算子保持規範不變性,還要再加上定義如下W(ξ-,0)
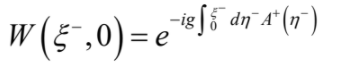
A 代表的是膠子場。這是所謂的Wilson Line。它代表的是帶著xp動量的部分子與質子的其他部份交換低動量平方的膠子的效應。一般我們會選擇光錐規範條件:A+ = 0,這樣Wilson Line 等於1就可以不必理會它了。不過在更一般的情況,就沒辦法不管它了。後頭我們會再討論它的。
雖然PDF的研究已經持續了超過半世紀,不管是理論,還是實驗都累積了許多成果,然而所得到的基本上都只有縱向的資訊。至於橫向的資訊則是一片空白。但是若想要想擴展部分子的知識到橫向,卻比想像中困難多了。不只是實驗更加困難,就是在理論層面上也要複雜許多。這是由於在無窮動量座標系中,只有一個相關的能量規模,就是質子的動量p,所有的量都是以它為基準,這簡化了整個分析。但是一旦將橫向的分布放進考慮,等於引進了第二個的能量規模,這讓整個分析起了巨大的變化。此外還有一個重要的因素,就是夸克,膠子都是擁有自旋的基本粒子,所以就算我們不考慮部分子的橫向動量與位置,僅僅讓部分子的自旋指向與其動量垂直的方向,就會浮現新的困難。舉例來講,DIS即使在扭度展開的首階,也有三個不同的PDF,可以圖示如下

圖四:扭度展開首階的三種PDF

圖五:Chiral-odd PDF擷取需要helicity-flip 的過程
單單讓部分子的自旋指向橫向,就產生這麼大的困難,可以想像當我們把部分子的橫向動量考慮進來以後,會遇到多少的麻煩了吧。接下來我們就來介紹橫向動量相關的部分子分佈(Transverse-momentum-dependent parton distribution functions, 簡稱TMD-PDFs)。概念上TMD-PDFs 並不難理解,但是要給出一個在量子場論上準確的定義可沒那麼容易,重點在於非局所算子定義的兩點之間的橫向距離不再是零,經過傅利葉變換就可以得到TMD-PDFs。
圖六:TMDPDF 的Wilson Line 路徑與時間反轉
依照質子與夸克的自旋指向,我們可以得到在扭度展開下的首階有八個TMD-PDFs。 f1,g1與h1這三個函數對部分子橫向動量kT積分以後就是原先的三種PDFs。此外還有五個新的函數,如果對對部分子橫向動量積分以後會得到零。其中受到最多注目的是Sivers 函數 f1T。這是橫向極化的質子的非極化夸克分佈。它之所以受到注目是因為它是naive T-odd。也就是說,乍看之下,在實行時間反轉的變換後,Sivers 函數會多出一個負號,既然QCD是時間反轉不變的理論,那麼Sivers 函數就該為零才對,但是這個推論忽略了一點,就是Wilson Line。先前我們提過,若是採用光錐規範Wilson Line的值為1,但是如果是連接Wilson Line的兩點有橫向位移的話,這個結論就不成立了,因為光錐規範無法完全決定膠子場,考慮Wilson Line的標準途徑,Wilson Line 會變成複數,在考慮時間反轉時,物理量要取複數共軛, Wilson Line提供的相位就使得Sivers 函數不為零也不會違反時間反轉不變性。除了Sivers 函數以外,Boer-Mulders 函數h1也是naive T-odd。基於相同原因,也不會因時間反轉不變性而被排除。Boer-Mulders 函數是非極化質子中橫向極化部分子的分佈,與Sivers函數恰恰相反。

圖七:八種TMDPDF 的名稱與性質
另外還有Pretzelosity 函數 h1T,它是chiral-odd 但是T-even的TMD-PDF。而worm-gear functions 則是指g1T與h1L。這個名稱是來自於靶與部分子的極化方向相垂直,有如變換方向的齒輪一般。一個是在縱向極化的質子中橫向極化夸克的分佈,另一項是橫向極化的質子中縱向極化夸克的分佈。這麼多未知的TMD-PDFs,要從哪些實驗數據來擷取它們呢? 主要是從兩種實驗來下手。一種是極化的質子的Drell-Yan 過程,另外一個實驗就是所謂的半包容性深度非彈性碰撞(semi-inclusive Deep inelastic scattering, 簡稱SIDIS)。前者的困難在於散射截面很小,測量不易。而且不同種類的夸克的貢獻加總在一起。後者的難處則在於散射截面是TMDPDFs 與 TMDFFs (Transverse momentum dependent fragmentation functions)的捲積(convolution)。所謂碎形函數 (fragmentation functions) 指的是動量為P的夸克放出動量為zP的強子的機率。一般是從正負電子湮滅成虛光子再對生正負夸克對,夸克與反夸克放出強子的過程來反推碎形函數。不意外的, TMDFFs 也有八種。其中最重要的,除了非極化的TMPFF,D1之外就屬科林斯 (Collins) 函數H1了。這是由於即使用非極化的電子與質子,散射截面中還是有一項是Boer-Mulders 函數h1與科林斯函數H1的捲積。

圖八:八種 TMD 碎形函數
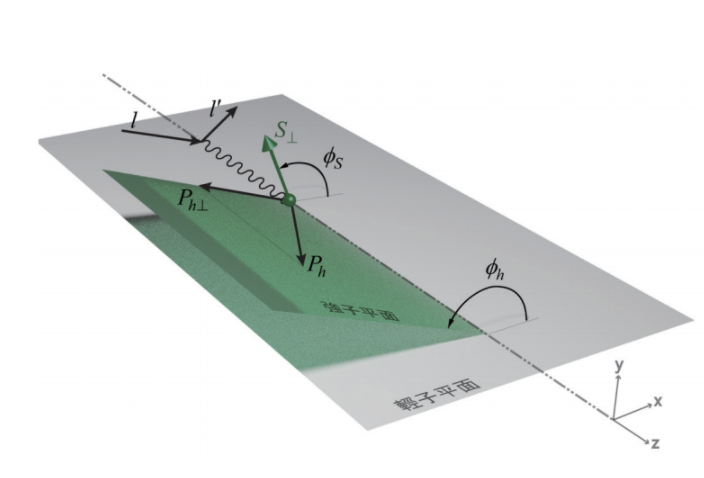
如果將質子橫向極化的話,可以由不同極化方向結果的差來擷取Sivers函數與D1捲積;Transversity 函數與科林斯函數H1的捲積,以及Pretzelosity 函數 h1T的捲積。第一個組合隨著sin(ϕh-ϕs),第二個組合隨著sin(ϕh+ϕs),第三個組合隨著sin(3ϕh-ϕs)。縱向極化的質子則能提供h1L與科林斯函數的捲積。若是同時讓電子與質子都極化的話,可以得到g1與g1T與D1的捲積。

圖九:SIDIS的運動條件。ϕh代表強子平面與輕子平面的夾角,ϕs代表質子極化方向與輕子平面的夾角。輕子平面是由輕子碰撞前後動量所張出的平面,強子平面是碰撞產生強子的動量與虛光子動量張出的平面。
至於Drell-Yan 過程中可以藉由質子極化方向來擷取Boer-Mulders 函數,Siversc 函數,Transversity 以及Pretzelosity 函數。從Drell-Yan 過程的結果來擷取的好處是不需要擁有任何碎形函數的知識。但是由於Wilson Line 的路徑與SIDIS不同的關係,物理學家預測由Drell-Yan 過程得到的Siversc 函數與從SIDIS得到的,會存在著一個負號的差異! 這個預測正初步與實驗結果吻合,但是仍需要更精確的實驗數據來支持。TMDPDF 如何隨Q2 演化是個理論難題,甚至將SIDIS的實驗條件並不是如DIS那樣容易判斷是否能採用“手提袋近似”,放出強子的夸克也未必是被虛光子打到的部分子,這都是TMDPDF 研究遇到的障礙,這些專門的問題,這裡就不多說了。
雖然有五花八門的TMD-PDFs, 但是這些卻沒有辦法告訴我們部分子在橫向位置上的分佈。所以我們需要從別的物理量來探索這方面的訊息。這個物理量稱之為廣義部分子分佈(Generalized Parton Distributions, 簡稱為GPD)。這個物理量是這樣定義的
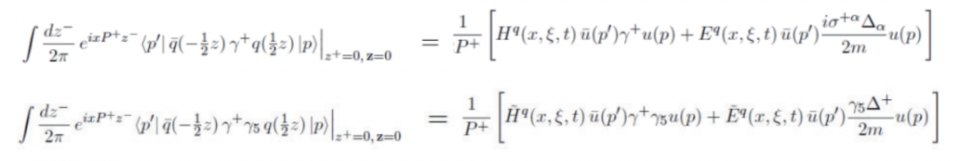
圖十:GPD的定義
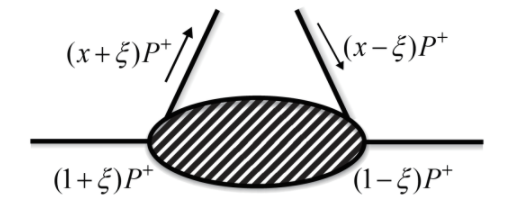
GPD與一般PDF 不同的是它是初態與末態不同的矩陣元素,所以要擷取這個物理量不可能仰賴包容性散射,而是必須從排斥性過程(exclusive process,也就是初態、末態都必須被測量,決定其能量與動量的散射過程)。而且它是三個變數的函數。在此P=1/2(p+p') ; ∆=(p−p') ; t=∆2 而下圖中 ξ =p+− p'+/ p++ p'+。粗略地講,GPD是從質子拿出一個夸克再放回去一個動量不同的夸克回去的機率。由於裡頭的算子是定義在光錐上,沒有橫向的位移,所以Wilson Line在此就不用去擔心了。
圖十一:GPD示意圖
GPDs 有許多神奇的性質。首先GPD提供了一個連接形狀因子與PDF的橋樑。當Δ=0, GPD 自然回到PDF。這個稱為forward limit。另一方面,如果我們講GPD對x作積分,從-1積到1,將會得到如下的結果:
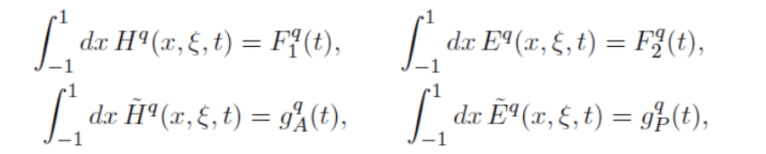
圖十二:形狀因子與 GPD 的關係。
GPD另外一個神奇的性質是H(t = 0) 與E(t = 0) 的和的二次矩居然等於部分子的總角動量! 事實上,部分子如何組合成一個自旋為二分之一的質子一直是強子物理界的一個大謎題。因為質子的自旋照理說是夸克的自旋角動量加上夸克的軌道角動量再加上膠子的總角動量,因為規範玻色子的角動量雖然可以分成自旋角動量與軌道角動量,但是這個區分是無法維持規範不變性的。從實驗中得知夸克的自旋角動量只貢獻了約莫百分之三十的質子自旋。所以膠子與夸克的GPD成了許多研究的焦點。此外,如果在ξ = 0,對初態與末態橫向動量差作傅利葉變換的話,就得到了部分子在橫向位置b 如何分佈的資訊了:
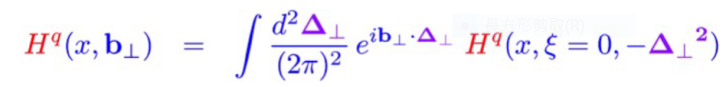
圖十三: GPD用撞擊參數表現的形式
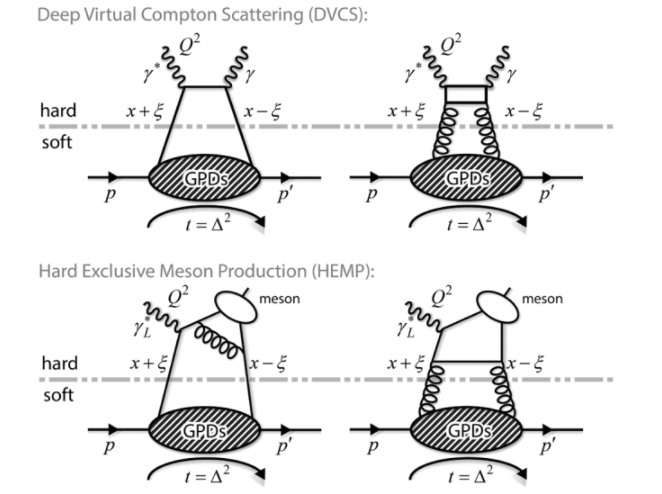
GPD的Q2演化比起TMDPDF單純多了,而判斷實驗條件是否符合手提袋近似也比TMDPDF來得容易,問題是擁有這些神奇性質的物理量GPD好不好量呢? 答案是非常困難。估且不論GPD本身是三個變數的函數,光是必須從排斥性過程的實驗來擷取就讓整個擷取過程變得比PDF困難多了。最常見的是從深度康普頓散射(Deep Virtual Compton Scattering, 簡稱 DVCS)的實驗結果來處理。DVCS是電子與質子交換一個動量平方很高的光子,然後質子釋放一個光子的散射過程。另外一個可能的實驗室光致介子生成(Hard Exclusive Meson Production)。

圖十四:GPD相關實驗(手提袋近似下)示意圖
利用DVCS的難處在於大部分的散射截面都是Bethe-Heitler (BH) 過程,即末態的光子從電子發出,而非從質子放出。所以科學家必須從BH過程與DVCS過程的干涉項來擷取GPD。另外一個問題是在DVCS中,個種夸克的貢獻都加總在一起。 從HEMP擷取GPD的問題則是散射截面與GPD的乘積有關,但在DVCS則是GPD與質子形狀因子的乘積。此外要從HEMP擷取GPD 還需要知道屆子的distribution amplitude(簡稱DA), 這又帶來新的麻煩。科學家努力擷取GPD也超過了二十年了,成果卻還遠遠部如PDF的豐碩,實在是個相當艱難的任務。

圖十五:DVCS 的散射
好奇的讀者也許會問,GPDs與 TMDPDFs之間有沒有什麼關聯呢?科學家發現可以最一般化的物理量稱之為Generalized Transverse Momentum Distributions (GTMD)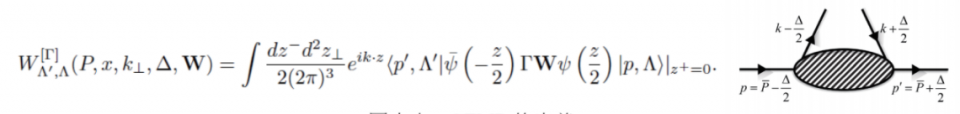
圖十六:GTMD的定義
將Z1取作零 GTMD即是GPD,但若是將Δ取作零,則是TMDPDF,所以其實這兩種物理量都是一個更一般物理量的兩個面相,所以GPD 與TMDPDF提供的是互補的訊息。而即將開始建造的EIC(電子-離子對撞機),它的科學任務就包含了提供更多質子內部三維的資訊,也就是它將進行更多與TMDPDF與GPD的相關實驗。而且它也將釐清質子中的膠子扮演的角色。EIC還將進一步研究原子核的部分子結構呢。也許有朝一天,物理學家能描繪出GTMD的完整面貌,給出完整的質子三維圖像,不過這還有待未來世代科學家的努力了。作者:高崇文 教授中原大學物理系