
量子四書(下) 從矩陣力學到量子場論
- 阿文開講
- 撰文者:高崇文
- 發文日期:2019-05-10
- 點閱次數:2908
上次阿文介紹了兩本source book,談到了從舊量子論到發展出矩陣力學的那一段過程,這次要接著介紹從矩陣力學到量子場論的這一段發展歷程,順便再介紹另外兩本source book。
上次提到由 B.L.Van Der Waerden 所編纂的 "Sources of Quantum Mechanics"的前十一篇都是與舊量子論相關,而第十二篇則是矩陣力學的開山之作。如果大家衝著"量子力學的奠基之作"這樣的名號去讀它,十之八九會跟少年阿文一樣,讀得一頭霧水。別氣餒,當年當海森堡寫出這篇文章時,他恐怕也不是那麼清楚他自己在幹嘛呢!據說他在投稿前還將論文草稿寄一份給他的老闆波恩看,他希望波恩決定要不要發表這一篇他自己都覺得"瘋狂"的論文,結果波恩看完以後受到很大的震撼,不僅要海森堡快快投稿,甚至自己跳下來跟著海森堡一起思考海森堡的新發現,到底這篇文章寫了什麼呢?
如果接著之前Kramers 與海森堡合寫的色散理論的論文來看的話,海森堡"似乎"只是重覆地得到了先前的結果,但是骨子裡頭卻大不相同喔!Kramers的做法是"假設"原子裡有許多"虛振子"在振動,利用古典力學得到振子的運動解,再利用量子化條件將"微分"改成"差分"而得到,但是海森堡主張量子物理需要的是一套新的"運動學",而不只是一套新的動力理論,這是只有二十五歲的少年郎才會講的"狂言"吧。他的作法是卻是將電子的位置寫成一個兩個指標的量(這是整篇文章最要緊,卻也是最難理解的地方!) 接著他利用量子化條件,直接就得到色散理論的公式!
問題是,電子的位置怎麼會有兩個指標呢? 這個古怪的想法源頭是來自於波爾的對應原則。技術上如果要利用波爾的對應原則,就必須對電子的運動做傅立葉分析,而傅立葉係數就對應到躍遷的機率。一般的傅立葉分析中出現的頻率都是某一個基本頻率的τ倍,τ是整數,而傅立葉係數Cτ對應的是從n 到m的躍遷,如果τ=n-m的話。但海森堡注意到,電子的運動頻率總是有兩個指標,因為波爾模型中的關鍵公式(稱之為波爾-愛因斯坦公式):
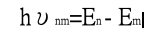
海森堡認為電子一定以這些頻率在作振動,既然電子的運動頻率總是有兩個指標,電子運動的傅立葉係數也理所當然應該有兩個指標,但是先前的想法是兩個指標是對應兩個"穩定軌道",原先的舊量子論是認為電子在幾個特別的軌道上穩定地運行,保持特定的能量,當電子"神秘"地發生躍遷時發出與能量差相等的電磁波,就在此處,海森堡作出最為關鍵的突破!他把原先波爾模型中的"軌道"先拋在一邊,接著他反其道而行,讓我們假設電子的運動是由這些特定頻率υnm的運動所組成的,那麼發生從n到m的躍遷機率自然是頻率υnm 相應的傅利葉係數Cnm , 只要將先前的量子化條件改寫成Cnm 必須滿足的限制,再加上古典電動力學中輻射的公式,海森堡就可以得到先前Kramers 的結果了!尤其重要的是,輻射公式需要計算位置的平方,而我們可以發現,要讓頻率滿足波爾-愛因斯坦公式,直接相乘是行不通的,只有下列這種組合才行
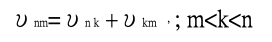
所以相應傅利葉係數的乘法也必須是
Cnm=Cnk x Ckm ,m
這正是矩陣的乘法! 矩陣力學之名也就是由此而來。(用今天的術語來講,海森堡在這裡"變"出來的矩陣是一個算子X夾在兩個本徵態:
[p, q]=pq-qp=h/2πi
這裡的p是動量而q是位置,但是兩者在量子理論中都是矩陣!這篇論文將矩陣力學的輪廓給鉤勒了出來,正如同這篇文章的標題"On Quantum Mechanics"一般,接著海森堡與波恩以及Pascal Jordan再合寫了一篇更完整的論文,被稱為"dreimaennerarbeit"。這篇文章將先前波恩與Pascal Jordan的論文推廣到多個自由度系統,發展出一般的量子力學微擾理論,也建構了量子力學的角動量理論,甚至在文章中,還討論了如何量子化無窮多個自由度系統的理論,Jordan特別分析了如何量子化一根弦的運動,更進一步他還以位置與對量的對易關係解釋了之前愛因斯坦針對普朗克分布產生的能量漲落可以寫成兩項,一項看起來像是波動的行為,另一項卻像是粒子行為的奇特現象!這一篇"dreimaennerarbeit"可以說是正式宣告了矩陣力學的誕生,唯一沒有完成的是由矩陣力學推導出氫原子能階。很快地這個艱巨的任務也被完成了!誰能完成這麼高難度的工作呢? 正是海森堡的師兄包立。第十六篇文章正式包立以矩陣力學的方法完整解出在庫倫位下的能量本徵值。包立還順手也把原子中的電子在外加電場(Stark effects)與磁場(Zemman effect)也算出來啦!此外這本書還收錄了兩篇狄拉克的文章,當時狄拉克還是劍橋的博士生,他發現了Hamiltonian Mechanics 中的Poisson bracket 與新發明的矩陣力學的對易關係根本遵守相同的代數關係,很快地這個沉默寡言的英國年輕學者成為量子物理的新星了!
量子力學出現後當然馬上有許多運用,然而引發量子革命的導火線終究是輻射問題,所以自然而然,電磁輻射如何被量子化是無可迴避的問題,而結果就是量子電動力學的誕生。接下來阿文要介紹的第三本Source book是由Arthur I. Miller 編纂的"Early Quantum Electrodynamics"。這本書說是Source book 還不如說是一本專門討論當年量子電動力學是如何萌芽,而又是如何與理論中陰魂不散的"發散"搏鬥的一本專門論著。這本書知道的人不多,但是阿文極力推薦。因為作者雖然是MIT的物理博士,卻變成專業的科學史學家,對於理念發展的歷史格外注重,所以常有別的書沒有提到的有趣論點。他特別重視海森堡與包立與其助手之間的互動,還常引用他們之間的通信,比起一般的Source book,這本書更像是一本科學史專著。而且收錄的文章凡是原文不是英文的都被翻成英文了。不過美中不足的是它在前面介紹中提及的文章,都沒有收錄在書中,反而是在許文格所編纂的那本赫赫有名的"Selected paper on Quantum Electrodynamics"裡頭可以找到,所以看官們可以參照地看,當然許文格這本書的視野不限於早期的量子電動力學,我們後頭還會再細細介紹它。

許文格(圖片來源:wikimedia common)
"Early Quantum Electrodynamics"這本書在簡單介紹量子力學的歷史後,第二章一開頭就提到了dreimaennerarbeit 中Jordan的工作,接著就介紹了狄拉克在1927年發明的電磁場的量子理論,(這一篇文章收錄在許文格的書中,而且排在第一篇!) Jordan將狄拉克的方法推廣到質量不為零的波色子,並與Wigner 一起將這個方法推廣到費米子。(這一篇也收錄在許文格的書中,第四篇),但是Arthur I. Miller 卻特別重視Jordan 與Klein 在處理波色子的庫倫自身能時利用改變算子排列的次序來削去一些無窮的技法,這個方法後來被系統性的發展,現在被稱為Normal order。第三章則是介紹狄拉克的相對性電子方程式以及狄拉克為了解決負能量的問題而引入了電子海的概念,以及在1931年狄拉克提出了電子的反粒子"正子"的概念。中間還穿插了海森堡與包立在1929年嘗試利用拉格蘭日公式寫下最早的量子電動力學,而且他們一開始就遇到了電子自身能發散的問題。Arthur I. Miller 收錄的第一與第二篇文章都是海森堡寫的相關文章。在這裡作者還簡單地介紹了二十世紀初羅倫茲等人從電磁輻射發展出的"電磁質量的概念。第三篇與第四篇則是狄拉克的正子理論。第三篇同時也收錄在許文格的書中,卻是法文。這一篇提出一種新的效應,就是電磁場引發正負電子對生旋即湮滅而造成的真空極化效應,而這個效應用量子電動力學一算,也是發散!
第四章則是正式介紹量子電動力學,作者著墨於高階計算出現的各種發散的問題。比較特別的是他特地介紹了狄拉克與海森堡早期嘗試利用重新定義算子乘積的方法來削去這些發散的工作,其中海森堡的文章被收錄,列在第六篇。此外還有包立當時的助手Weisskopf 用狄拉克發展的電子海理論分析電子自身能發散的論文,這一篇收錄在書中(第五篇),然後還提到了包立與Weisskopf重新讓Klein-Gordon 方程式復活的故事。這一篇也有收錄,是第七篇。這個故事各位看官不妨參考阿文之前寫的"自旋物語"一文。
比較稀奇的是這本書的作者還提到了海森堡與Euler 研究光與光的散射,還寫出有名的Heisenberg-Euler Lagrangian,這本書收錄的第八篇文章是Weisskopf一篇非常漂亮的論文,他用很簡單的方法得到了海森堡與Euler的結果,這一篇也被許文格收錄在許文格的那本書中,卻是德文。至於Arthur I. Miller收錄的第九篇論文則是包立與他的助手Marcus Fierz處理所謂"紅外災難",也就是在末態的電子發射無限多個能量無限小的光子的問題,一般大家熟知這個問題是由Felix Bloch 與Arnold Nordieck 首先找到解決的方法的,而第十篇文章則是海森堡試圖引入一個新的"universal length" 來解決量子場論的發散問題,當然,這想法並不奏效。最後一篇文章則是H. A. Kramers 在1937年發表的一篇提倡"再重整化"的短文。Kramers 特別主張實驗上量到的電子質量是電子的"力學質量"以及"電磁質量"的總和。量子電動力學中出現的無限大自身能是"電磁質量"的一部分,但是Kramers 認為電子的力學質量是一個只出現在拉格蘭日函數的數字,而這個數字如果是無限大的話,由於電磁質量與力學質量的正負號相反,很有可能可以得到一個有限的"總質量"。這個聽起來非常古怪的建議在戰後扮演了一個關鍵的角色,但是Arthur I. Miller的書只談到這裡為止,接下來的發展,阿文要鄭重推薦許文格編纂的這本 source book, "Selected paper on Quantum Electrodynamics"。當年阿文第一次接觸量子電動力學,看的就是這本書!

許文格編的這本書收錄了三十四篇文章,時間從1927年到1953年,可以說涵蓋了量子電動力學整個發展的過程。前面許文格只寫了十一頁的序當作介紹,卻稱得上是字字珠璣。前面九篇基本上是戰前量子場論的發展,第九篇正是Felix Bloch 與Arnold Nordieck 解決紅外災難的論文。從第十篇開始則是量子電動力學在戰後的發展記錄。
首先上場的是兩篇實驗的文章,第十篇是H. M. Foley 與 Polycap Kusch 寫的有關電子的磁偶矩測量的結果。Polycap Kusch 出生於德國,後來全家移民到美國的美國物理學家,當時他在紐約的哥倫比亞大學,在拉比的指導下從事分子束的實驗,拜戰時長足進步的微波技術之賜,讓他發現了電子的磁偶矩與狄拉克方程式所預測的值有非常微小的差異。而第十一篇則是威廉‧蘭姆與Robert C. Retherford 有關蘭姆位移的實驗結果。蘭姆位移是兩個氫原子能階,2S1/2 與 2P1/2之間的能量差,這兩個能階依照狄拉克方程式的計算結果應該是相同的,所以量子電動力學如果不能解決原先的發散問題,就根本無法解釋這兩個現象了,這就是觸發戰後量子電動力學突破性發展的機緣,科學就是這樣子,有挑戰,才有回應!
第十二篇是H.A.Bethe 在開完Shelter Island 會議在回程的火車上嘗試將Kramers 的想法落實的結果,他利用非相對性量子力學算了自由電子與束縛在氫原子中的電子的自身能的差,雖然這兩者的自身能都是發散的積分,但是它們的差卻是有限的,更要緊的是這個差與隨著電子能階不同而有所不同!如此一來,這個效應就足以來解釋原本簡併的兩個能階會產生能量差。Bethe 估計高能量光子的貢獻是與虛光子最高的能量成對數的關係,這是之前Weisskop的論文就推導過的結果,照理說這個截止的電子能量應該是無限大,但是Bethe隨意地取了一個能量上限,mc2 (m 是電子的質量),卻神奇地給出1040MHz的答案!(當時的實驗值是1057 MHz!)這篇短短三頁的論文卻接著兩篇分別只有一頁與兩頁的論文,而且都是許文格自己寫的論文!第十三篇是許文格以類似的方法求得電子磁偶矩的精確值的報告,而第十四篇則是在庫倫力場下電子散射的輻射修正,但是在這一篇文章的腳註中,許文格卻宣稱這個計算中為了讓結果滿足相對論不變性,他必須加上一項額外的磁偶矩的貢獻,這是因為與Bethe一樣,許文格在此的計算並沒有真正滿足相對論不變性,而第十五篇則是歐本海默在1948年Solvay 會議的報告,這篇報告簡明地總括了Bethe與許文格的成果,卻也指出必須發展出擁有相對論不變性以及規範不變性的完整量子電動力學計算的重要性。
當然,許文格後來的確發展出擁有相對論不變性以及規範不變性的完整量子電動力學,但是第十六篇他卻是放了朝永振一郎有關"超多時間理論"(super-many-time theory)的論文,(名字聽起來很酷,但其實它只是一個將Hamiltonian formalism 改寫成一個明顯滿足相對論不變性的形式而已啦) 而接下來這篇才是整本書的最高潮,許文格用擁有相對論不變性以及規範不變性的完整量子電動力學去計算電子散射的輻射修正項。但是各位看官要是興沖沖去讀的話,我保證你大失所望,因為這是一系列文章的最終章,但是前兩篇許文格卻沒有將它們收錄進來,你得自己把它們找出來先好好研讀一番,才知道第三篇在幹嘛!阿文一直覺得編者好像在跟讀者開了一個玩笑一般。(阿文當年當兵時把這三篇論文放在枕頭下讀了兩年,可以說是刻骨銘心的回憶呢。)
接著是一篇一頁的短文,作者又是朝永振一郎,主要是概述他們得到與許文格一樣的結果。第十九篇則是包立與助手F. Villars 一起發展出對付發散積分的數學技巧,好處是比起直接放個積分上限的土方法,這個新方法可以維持規範不變性,再來則是許文格寫的非常優美的名文:" 論規範不變性與真空極化",關於這一篇,阿文建議讀者參考孤高的物理學家:許文格(三) 獨向斜陽嘆白頭,那裡有詳細的介紹。這裡就不多說了。
截至目前,怎麼都沒看到另一位主角費恩曼的蹤跡?別急,從第二十一篇開始,連續三篇都是費恩曼的大作,接著兩篇則是F.J.Dyson 的文章,證明費恩曼的方法與許文格以及朝永振一郎的方法是等價的。對現代的讀者而言,這五篇文章簡直是久旱逢甘霖,一下子見到老朋友的感覺油然而生,阿文記得第一次讀這本書實是升大四的暑假,讀到這裡才稍稍恢復信心,總算有看得懂得東西出現了! 接著許文格又放了狄拉克一篇關於量子力學與拉格蘭日力學的關聯的文章,這文章可不得了,因為費恩曼的量子力學的路徑積分公式以及許文格的量子作用量原理都是從這篇文章得到靈感的。所以順理成章,接下來三篇文章分明就是費恩曼與許文格的文章。第三十篇是包立寫的自旋統計定理,而接在後頭的卻是許文格的格林函數的文章,然後是許文格的兩個助手Robert Kaplus 還有Abraham Klein 算Lamb位移算到下一階的文章,最後一篇則是William M Kroll與蘭姆合寫關於蘭姆位移計算蘭姆位移的文章,許文格還特別注明這一篇應該排到第十三篇,卻"for reasons beyond my editorial control",被放到最後,不知道背後有沒有故事呢?
回頭看這四本source book, 阿文真心覺得現代的讀者真是幸福,過去要親炙這些大家文章,得靠這些編者的精心選擇,現在網路世界四通八達,要看什麼文章都不費吹灰之力,但是阿文卻很少聽說有年輕學子願意去一探量子理論的究竟,在此野人獻曝,希望有年輕學生,在看完阿文的介紹後,也能發願好好拜讀這些原始論文,感受一下,這場人類史上少有的驚濤駭浪的知識革命帶來的衝擊!尤其是當時的科學論文寫作還蠻重視風格的,在講求時效的今天,科學論文愈來愈技術化,也愈來愈索然無味,能夠讀一些"名文",對提升自己的物理品味,也是會有幫助的!
延伸閱讀
量子四書(上) 從量子論到量子力學