
相對論裡的兩種時間 — 淺談孿生子悖論
- 皮皮老師的物理心得
- 撰文者:欒丕綱
- 發文日期:2021-04-08
- 點閱次數:5989

狹義相對論發表至今已經超過一個世紀,它所帶來的時空觀念與相關的物理效應也早已是近代物理教科書裡的標準內容。透過推導羅倫茲轉換或是學習時空圖 (space-time diagram),要掌握這個時空觀念並不困難。很多的 Youtube 影片對相對論的科普也做出了貢獻。不過,在面對這些跟日常經驗衝突的觀念時,難免會讓人感到困惑。人們在理智上很容易接受科學實驗的結果或是權威的意見,但在心理上或許較難被理論本身的邏輯結構說服。在本文中,筆者將對狹義相對論 (special relativity) 裡的時空概念與「孿生子悖論」(twin paradox) 問題做一番分析,希望能讓更多朋友理解相對論的邏輯內涵與物理概念。
首先從日常生活中的時間的概念談起。一般人對時間的熟悉程度應該已達到可以不假思索地運用自如的地步。當兩個信守承諾的朋友相約「明早九點咖啡館見」時,他們會預期當他們的手錶在明天上午顯示九點整時,在他們相約的咖啡館裡一定可以見到對方,而此刻咖啡館裡的時鐘一定會正常顯示著九點,除非那個時鐘壞了,或是之前就沒有對準。當一個人要去某地處理事情,出門前他先比對自己的手錶與網路上的時間,發現都是下午三點鐘。當他到達目的地,手錶顯示下午五點鐘。此時若檢查網路時間,一定也會是五點鐘,除非他的手錶壞了。
當我與倫敦的朋友在線上討論問題時,我知道我們的時鐘顯示的時間因不同時區而差了八小時。我們只要做一個加減八小時的簡單轉換,就可以認同彼此是在「相同的時間」討論問題。此外,我在台灣過了一秒鐘,他也會過一秒鐘。我不會看到他以慢動作行動或是增速跟我講話,除非網路有訊號延遲的問題。好天氣的日子裡,當我望向太陽時,我知道我看到的是它在 8 分 20 秒前的樣子,因為太陽光傳到地球需要花這麼多時間。只要把這時間差修正掉,就可以談論地球與太陽在「同一個時間」發生的事情。而我會很有信心地認為地球上的一秒與太陽上的一秒並無不同。
在上述這種簡單的時間觀念裡,時間是一個放諸四海皆準的概念,具有絕對性,與我們使用移動的手錶還是固定在車站的時鐘測量時間並無關係。這個絕對時間的概念,搭配上剛體 (rigid body) 具有絕對長度的概念,就導出了以下的伽利略轉換 (Galilean transformation):

這個轉換說明的是在兩個彼此有相對速度的慣性參考系 (inertial frames) S與 S' 中進行物理測量時,兩系對「同一地點,同一時間」的事件 (event) 測得的空間座標與時間座標的轉換關係。在轉換式中,我們假定的 S' 系相對於 S 系的速度 v 是在 x 方向,而兩個參考系的座標軸平行或重合,設定如下圖:
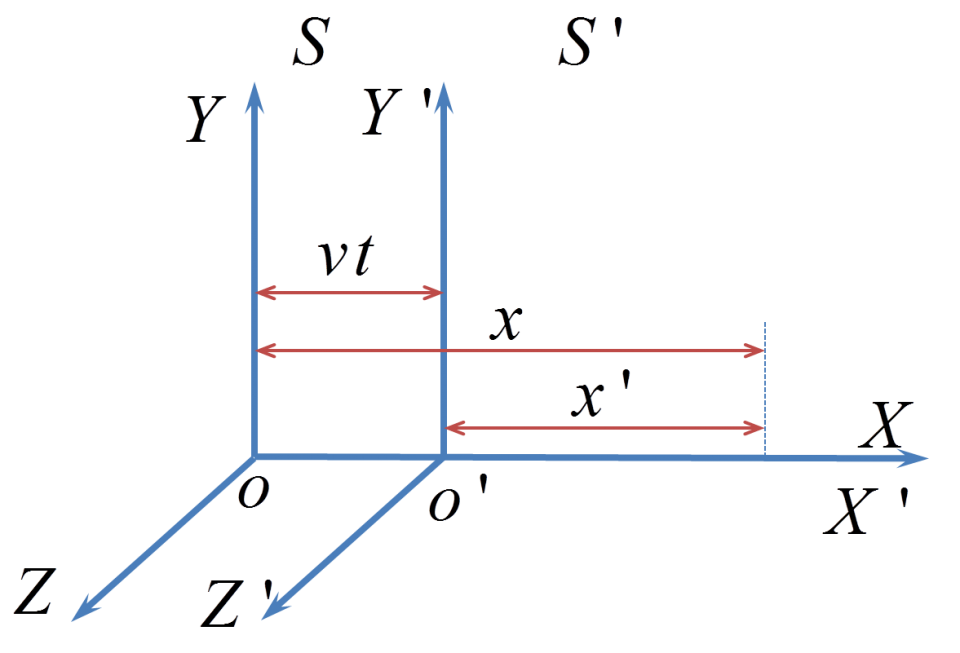
這裡所謂的慣性系指的就是牛頓的力學定律可以直接在其中應用的參考系。轉動或直線加速的參考系都不在此列。我們也可以根據伽利略轉換得出在兩參考系中觀測同一個運動物體的速度轉換關係,其結果就是平常熟知的速度合成定律。
由伽利略轉換得到的一個最重要結果就是所有慣性參考系在力學現象上都是等價的。牛頓力學三大定律以及萬有引力定律在伽利略轉換下都不會改變形式。所以要藉著力學實驗給出唯一正確的慣性系或絕對空間是做不到的,所有慣性系都一樣好。19 世紀時,物理學家把伽利略轉換應用到電磁學與光學問題時,發現不同的慣性參考系在理論上是可區分的。這暗示慣性系的絕對運動速度或許可以藉由光學與電磁現象的觀測間接測量出來。當時的人們相信宇宙中充滿了一個叫以太 (ether) 的介質,而光波就是藉著它才能傳播的。如果以太存在且伽利略轉換正確,就可以藉著在地球上測量不同方向的光速差異推論出地球在太空中的運動速度。不過,這類的實驗最後都失敗了,測不出預期的差別。此外,在低頻的電磁現象中 (例如線圈與磁棒的相對運動導致線圈中出現感應電流),在相對運動的兩個慣性系中所觀察到的現象並沒有區別,雖然可能採用不同的觀念解釋此現象。上述這些情況暗示以下兩個結果:
愛因斯坦於 1905 年,在論文《論動體的電動力學》中就是將這兩個由實驗與觀測歸納出的線索提升為基本假設,進而推導出新的時間與空間座標轉換定律,再利用這個新的轉換定律修正了牛頓定律與重新詮釋了電磁學,其結果就是狹義相對論。這個新的座標轉換關係式被稱作羅倫茲轉換 (Lorentz transformation),事實上是羅倫茲先導出的,但是第一位對它給出可操作的物理詮釋的卻是愛因斯坦。
羅倫茲轉換的具體形式如下 (推導細節請參考拙著《狹義相對論的時空觀》,科學月刊552 期, 942-945 頁 (2015)):

這裡的 c 是真空中的光速,而 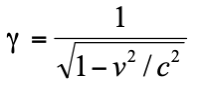 是一個很關鍵的「膨脹因子」(expansion factor)。當參考系的相對速度 不為 0 時,這個因子會比 1 大。有趣的是,電動力學的馬克斯威爾 (Maxwell) 方程組在羅倫茲轉換下形式不變,因此電動力學是一個純天然的相對論性理論,不需要修正。愛因斯坦發現,在探討動體電動力學時,以太是可拋棄的。有些人說以太被相對論否定了,事實上以太並沒有被相對論否定。正確的說法是它在羅倫茲轉換下是「不相關」或「無影響」的。愛因斯坦自己在「論動體的電動力學」(1905) 的說法是:『光以太的引用將被證明是多餘的…』。
是一個很關鍵的「膨脹因子」(expansion factor)。當參考系的相對速度 不為 0 時,這個因子會比 1 大。有趣的是,電動力學的馬克斯威爾 (Maxwell) 方程組在羅倫茲轉換下形式不變,因此電動力學是一個純天然的相對論性理論,不需要修正。愛因斯坦發現,在探討動體電動力學時,以太是可拋棄的。有些人說以太被相對論否定了,事實上以太並沒有被相對論否定。正確的說法是它在羅倫茲轉換下是「不相關」或「無影響」的。愛因斯坦自己在「論動體的電動力學」(1905) 的說法是:『光以太的引用將被證明是多餘的…』。
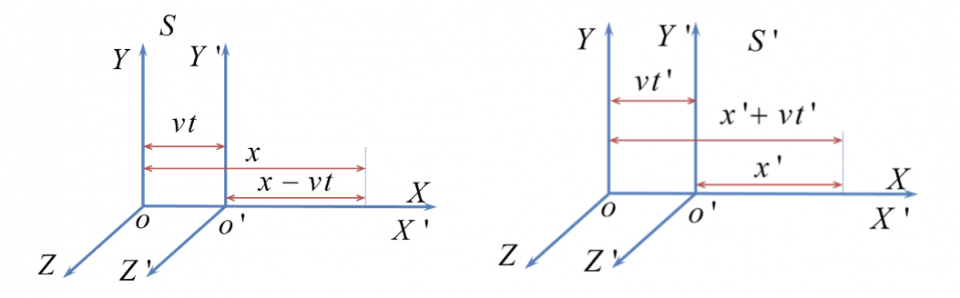
圖3. 羅倫茲轉換。左圖與右圖分別為S系與 S' 系的觀測結果。此兩圖沒有標示出座標時鐘的刻度。在系中的同一個時刻,會因位置不同而對應系裡不同的時間,反之亦然。
愛因斯坦在推導這組轉換式時,其實假定了在慣性系 S 與 S' 中處處都安排有時鐘與觀察者,而每一個觀察者只需負責記錄發生在自己身邊的事件所對應的眼前時鐘的讀數。在做物理觀測之前,必須先校準時鐘,使得我們在這個參考系中說「現在是兩點整」有意義。首先可選擇參考系內某一個時鐘為標準時鐘,然後發送光訊號給參考系內另一個觀察者。考慮傳播過程的時間差 (距離除以光速 c),透過兩方的溝通就可以校準這兩處的時鐘,使它們同步化。重複使用這樣的校準手續就可以校準參考系內的每一個時鐘,達到所有時鐘的同步化,然後就可以用這些時鐘來記錄時間了。此處比較微妙的是這個「校準手續」只有在同一個慣性系裡看起來是有效的,換到其它有相對速度的慣性系裡看來這些時鐘就都是沒校準好的。
以S'系的校準手續為例,由座標原點處的標準時鐘向正負 x' 方向同時發射的光訊號都是以光速 c 傳播,因此可以在相同時間間隔內傳到等距離的左右兩方時鐘。不過,由於 S' 系裡的時鐘相對於 S 系都以速度 v 向右 (+x) 方向運動,但是由 S' 原點發出的光相對於S 系仍然是以光速 c 向著左右傳播,因此在 S 系內觀測 S' 系的上述過程,會發現向右傳播的光是追著右側的時鐘跑,因而會晚一點到達右側時鐘。反之,左側時鐘是迎向左傳的光移動,因此光會提早到達左側時鐘。也就是說,在 S' 系中同時發生的兩件事,在 S 系中不是同時的。從S' 系觀察S系的時鐘校準也有同樣的現象。這個被稱為「同時的相對性」(The relativity of simultaneity ) 的現象,就是在羅倫茲轉換的時間轉換式 (第四列公式) 中會出現空間座標 x 或 x' 的原因。
利用羅倫茲轉換可導出非常有名的「動尺縮短」與「動鐘變慢」現象。考慮一把靜置於在 S' 系中 x' 軸上的尺,其左右兩端座標分別是 x1' 與 x2',因此這把尺在靜止時的長度就是
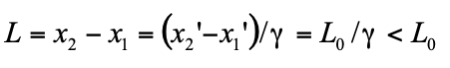
意即運動的尺比較短。從這個推導中,讀者應可看出這個長度收縮 (length contraction) 效應與前述「同時的相對性」有著非常密切的關係。如果我們考慮的是一把靜置在 S 系中的尺,然後在 S' 中的同一時間觀察其兩端的座標,我們也會得到直尺變短的結論。讀者或許會問:如果 S 系與 S' 系各有一把同樣的尺 (第三方造好後分別交給兩個系),當它們彼此滑過對方時 (只發生一次,不回頭),究竟哪一支尺比較短?答案是雙方都發現對方比較短!讀者只要注意到「同時的相對性」在此發揮的作用,就可以理解為何這是沒有矛盾的了。
接下來談談動鐘變慢。考慮在 S' 系的原點 (x'=0) 觀察一個從t1' 時刻進行到 t2' 的物理過程,它在持續的時間間隔是T0=t2'-t1'。將 x'=0 代入羅倫茲轉換的最後一式,就得到此過程在 S 系中對應的時間間隔是
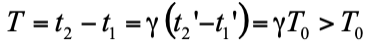
這就是所謂的時間膨脹 (time dilation) 效應。此處「膨脹」所指的是在兩個不同地點的時鐘的時間差 (在 S 系內的觀測結果) 會比那個經過它們的單一時鐘自己記錄的讀數差 (S' 系裡的觀測結果) 要長,亦即運動的時鐘 (因移動而有改變地點的那個時鐘) 比較慢。像前述的動尺縮短效應一樣,若觀察 S 系裡的單一時鐘記錄的時間,也會比它先後經過的 S' 系的兩個座標鐘的讀數差要短。因此,時間膨脹在慣性系之間是相對的,沒有「誰真正比較慢」的問題。這個結果乍看之下難以置信,但只要記得這裡的比較指的是單一時鐘與它所經過的一系列時鐘相比較,而不是兩慣性系各拿一個時鐘來比快慢,就不會有矛盾了。用一個口訣就可以描述這個情況:我比「你們」慢,你也比「我們」慢。對此還有困惑的朋友,可以回頭再想想「同時的相對性」。
單一時鐘或手錶 (無論它怎麼運動或靜止) 所記錄的時間通常稱為「固有時」或「原時」 (proper time),而固定在慣性系中的無數座標時鐘所記錄的時間稱為「座標時」 (coordinate time)。原時可以說是一種「私有時間」,而座標時是「公共時間」。在相對論之前,人們不經意地假定了這兩種時間是沒有差別的,換了不同的慣性系也不會有差別。不過,正如前面所介紹過的,利用這樣的觀念所導出的伽利略轉換與速度合成定律在電磁現象與光速問題上導致了與實驗結果不合的預測。將慣性系之間的時空座標轉換改為羅倫茲轉換後,電磁定律與光傳播問題都給出與實驗一致的結果。當物理現象不牽涉到接近光速的現象時,羅倫茲轉換會退化為原來的伽利略轉換,因此也不會與低速情況下的牛頓力學矛盾。在高速的情況下,對牛頓力學的修正導致了關於質能關係式 E=mc2 的發現。這方面的故事將來有機會再跟讀者介紹。
現在來談談什麼是時空。考慮兩個事件 (events) 1 與 2,它們在慣性 S 系的空間與時間座標間隔記為 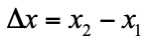 ,
,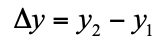 ,
,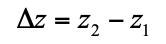 與
與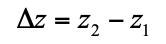 ,而它們在中的對應量是那些有撇號的量。根據羅倫茲轉換不難驗證以下等式成立:
,而它們在中的對應量是那些有撇號的量。根據羅倫茲轉換不難驗證以下等式成立:
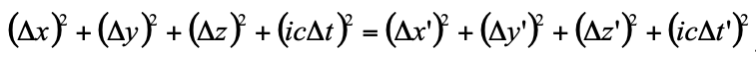
如果把 S 系到 S' 系的座標轉換視為一個四維歐幾里得空間 (Euclid space) 裡在座標旋轉下的距離不變性,那麼時間與空間就一起構成了一個四維的時空 (space-time),而兩事件間的「時空距離」可以定義為:
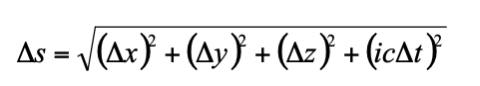
而此距離不因參考系的選擇而變。在這套時空語言裡,時間與空間可看成只是時空的投影,是與參考系有關的相對量,而時空距離是與參考系無關的不變量。不過,這個被稱為閔可夫斯基空間 (Minkowski space) 的四維時空具有不同於四維歐幾里得空間的幾何性質 (注意根號中的 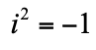 ),例如兩事件之間的時空距離的平方值可以是正的、負的或是0,但在真正的歐幾里得空間中的距離平方一定是正數或 0。將不變量
),例如兩事件之間的時空距離的平方值可以是正的、負的或是0,但在真正的歐幾里得空間中的距離平方一定是正數或 0。將不變量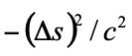 開根號可以定義另一個具有時間因次的不變量:
開根號可以定義另一個具有時間因次的不變量:
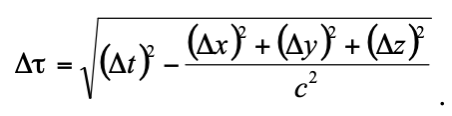
很明顯,若此兩事件分別代表運動時鐘「出發」與「到達」某地點,則此就是此一運動時鐘所記錄的原時!雖然在任意慣性系測量這一個運動時鐘有不同的速度與軌跡,但是所有慣性系對這個運動時鐘都會推算出完全相同的原時間隔,就跟它自己記錄的一樣。根據上述的原時公式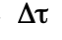 一定會小於或等於
一定會小於或等於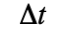 。所以動鐘記錄的固有時會比沿途所經過的座標時之差來得短。
。所以動鐘記錄的固有時會比沿途所經過的座標時之差來得短。
事實上,這個結論並不受限於等速運動的情況。一個非等速運動的時鐘在每一瞬間都可以被視為靜止於一個與它同步運動的慣性系中,累積一段極短的原時間隔。因此動鐘累積的總原時就等於每一瞬間累積的小段原時的總和 (積分)。由此可以推論出一個手錶若從某慣性系的原點出發,進行極高速度的旅行,當它最後繞回到出發點時,全程累積的原時間隔會比該慣性系的時鐘所記錄的數值少,也就是手錶絕對地變慢了 ! 把手錶與慣性系原點處的時鐘分別換成一對孿生兄弟,慣性系換成地球,手錶的運動視為太空旅行,就會得到一個有趣的結論:太空旅行的那位孿生子回到地球後會比他留在地球的雙胞胎兄弟年輕。
讓我們稱留在地球上這位為 A,星際旅行的那位為 B。相對於 B,A 也是以極高的速度在運動,難道不該是 A 比較年輕嗎 ? 這個困惑就是所謂「孿生子悖論」。解決這個悖論的關鍵,是注意到 A 處於慣性系之中,但 B 不是。因此他們的地位是不對等的。A 可以直接判斷 B 經歷的原時比較短,而且所有其他慣性系都會同意他的結論,無論它們相對於 A 是否有速度。反之, B 找不到這樣的「慣性系同盟」。說得直接一點,B 其實沒有說話資格,因為時空距離或原時的度量標準是由慣性系訂出來的。有一種說法是說因為 B 經歷了加速度,而加速度等效於重力場,所以必須用廣義相對論才能解決這個問題。其實這是不必要的。這種來自於火箭推進器的局部加速度並沒有造成時空彎曲,所以根本用不上廣義相對論的場方程式,因此使用狹義相對論就足夠了。加速度在此的意義並不在於減緩老化,而在於區隔哪一方才是慣性系。
讀者若還是對 A 與 B 的地位不對等有疑慮,可以想想牛頓力學中的轉動參考系。在這樣的參考系中出現的柯氏力與離心力,完全可以從慣性系中的力學結果經由座標轉換到轉動座標而得到,就像此處原時的計算是根據慣性系對原時的計算一樣。若讀者還是想知道根據加速系觀點所得到的原時是如何累積的,可以參考吳大猷教授的《相對論》一書 (理論物理第四冊,聯經出版)第五章,裡面有提供詳細的計算過程。
有一個重要問題在前面都沒有討論,那就是:究竟什麼樣的參考系才夠格稱為慣性系呢?地球顯然不是一個完美的慣性系,因為有自轉與公轉,而太陽系本身還繞著銀河系轉。不過,牛頓定律與馬克斯威爾電磁定律都是在地球上發現的,可見在適當條件下,地球可以視為是一個慣性系。關於慣性系的疑問把我們引向了與廣義相對論有關的觀念。我們以後再來聊這個主題。
作者:欒丕綱
國立中央大學光電科學與工程學系 副教授