
你是物理人還是電機人?談談複數物理量的表達習慣
- 皮皮老師的物理心得
- 撰文者:欒丕綱
- 發文日期:2021-01-04
- 點閱次數:8192
物理初學者可能會以為只有量子力學才會使用到複數 (complex number)。因為量子力學的狀態空間是抽象的希爾伯特空間 (Hilbert space),為了描述系統狀態在希爾伯特空間的演化必須使用複數,而古典物理的可觀測量都是實數,不需要使用複數。其實不然,古典物理與許多工程問題也大量使用複數表達式,雖然實際觀測的物理量確實可用實數表示。這些與實驗對應的實數量通常就是複數量的實部或虛部。在這些問題的處理中若完全不使用複數,解決過程就會變得非常繁瑣,有時候甚至根本做不到。舉例而言,像在「超穎材料」(metamaterials) 這類既有色散 (dispersion) 又有吸收 (absorption) 的介質中,介電常數 (dielectric constant, permittivity) 或磁導率 (permeability) 一般都是複數,而且不該把它們的實部與虛部拆開來看,因為彼此是互相關聯的。又例如要在波動光學 (wave optics) 範疇內解釋全內反射 (total internal refraction) 現象時,必須引入虛數的波向量 (wave vector),才能說明什麼是消逝波 (evanescent wave)。
在與振動、波動有關的問題中,為了描述振動或波動之振幅隨時間的變化,會遇到一個時間相關的相位因子 (phase factor),寫成
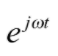 或
或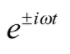 (1)。
(1)。
其中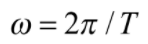 是振動的角頻率 (angular frequency),T 是振動週期,
是振動的角頻率 (angular frequency),T 是振動週期,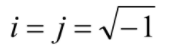 是虛數的基本單位。有趣的是,根據個人的觀察,我常常可以從這個因子的使用習慣判斷使用者的主要專業是偏向物理 (物理人) 還是偏向電機或工程 (電機人)。通常物理人會使用相因子 e-iωt,而電機人會選擇相因子 eiωt 或 ejωt。若是要描述一個向右 (+X 方向) 傳播的波,這兩種人群給出的表達式分別是:
是虛數的基本單位。有趣的是,根據個人的觀察,我常常可以從這個因子的使用習慣判斷使用者的主要專業是偏向物理 (物理人) 還是偏向電機或工程 (電機人)。通常物理人會使用相因子 e-iωt,而電機人會選擇相因子 eiωt 或 ejωt。若是要描述一個向右 (+X 方向) 傳播的波,這兩種人群給出的表達式分別是:
電機人: ψelec(x,t)=Aelecexp[j (ωt−kx)]. (2b)
其中 Aphys=Aeiδ, Aelec=Ae−iδ,A 與 δ 都是實數常數。當我們對以上兩種表達式取實部,會得到相同的瞬時波振幅
ψreal(x,t)=Acos(kx−ωt+δ), (3)
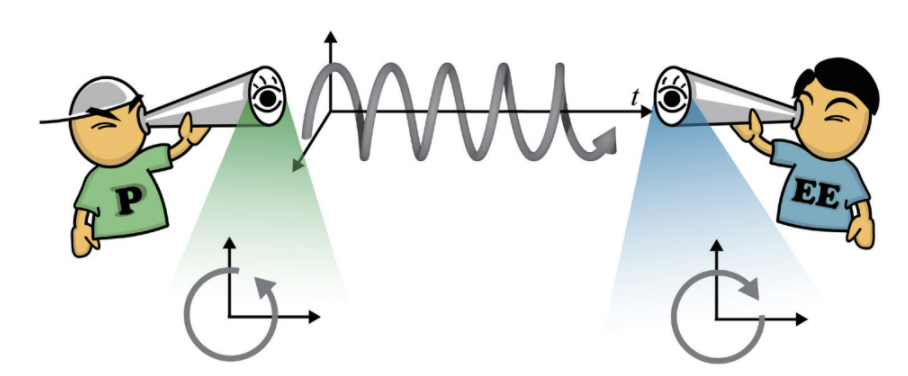
一個形如 Aexp(ikx) 的複數波振幅 ( 假定 k>0) 究竟表達的是向右還是向左傳播的波?這是沒有確定答案的,因為答案是由時間相因子的選擇所決定。當採用相因子 e-iωt 作為時間因子時,Aexp(ikx) 表示向右傳播的波,而 Aexp(−ikx) 表示向左傳播的波。反之若採用時間相因子 eiωt,上述的答案就要互換。一個更一般的情況是 k = kr+iki 同時含有實部 kr 與虛部 ki。當使用時間相因子 e-iωt 時,Aexp(ikx)=Ae−kixeikrx 配合條件 kr >0, ki > 0 代表一個朝右傳播並衰減的波。若時間相因子換成eiωt,則在同樣的條件下就必須改用 Aexp(−ik*x)=Ae−kixe−ikrx 才能表達同一個朝右傳播並衰減的波了。這個例子說明了採用複數表達式處理問題時必須很小心謹慎考慮我們採用的時間因子是什麼。當我們用錯了時間因子,就可能會對物理現象做出錯誤的推論。
那麼,是什麼原因導致物理人與電機人採用了不同的表達方式呢?對此我有簡單的解釋。先考慮以下一維單粒子系統的 “時間相關薛丁格方程式” (Time-Dependent Schrӧdinger Equation):
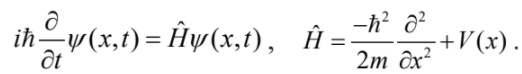 (4)
(4)上述問題中的定態 (stationary state) 波函數解ψ(x,t) 可以寫成
其中u(x) 是以下 “時間無關薛丁格方程式” (Time-Independent Schrӧdinger Equation) 的本徵函數 (eigenfunction) 解:
根據普朗克 (Max Planck) 的能量-頻率關係式 ,公式 (5) 可以寫成
ψ(x,t) = u(x)e−iωt, (7)
於是就出現了時間相因子e−iωt !另一方面,對於電機人而言,經常要處理時間訊號的傅立葉分析/轉換,採用相因子 eiωt將會十分自然。然而,由於 在電學裡面主要用來代表電流,所以將 i 換成j 會比較方便。這兩個簡短的觀察初步解釋了為何物理人與電機人會選擇不同的複數表達方式。
讀者或許會有一個疑問:如果當初薛丁格寫下的方程式在 (4) 式左方的係數不是 iћ 而是 −iћ,那麼物理人的時間因子不就變成跟電機人一樣了嗎?但是這樣修改過的薛丁格方程式是正確的方程式嗎?要解答個問題,可以對 (4) 式取複共軛 (complex conjugate)。這會使 i 改為 -i,且波函數 ψ 也被它的複共軛 ψ* 取代。根據這個觀察,可知將薛丁格方程中的 i 改為 −i 相當於用 ψ* 取代 ψ。這並不會改變與機率有關的描述,因為機率只跟波函數的絕對值平方 |ψ|2 有關。另一方面,在與波函數的干涉有關的現象中,觀測結果會跟參與干涉的各分波的相位差有關,而這個由 i 改為 −i 的操作會將這個相位差變號。若實驗結果只跟相位差的絕對值有關,這個修改並不會導致矛盾。不過,要正確表達動量算符 (momentum operator),必須配合這個修改將 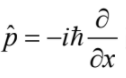 改為
改為 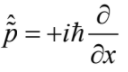 。這個關於動量算符表達式的修改也可以從位置-動量對易關係 (commutation relation) 的修改看出來。原來的對易關係是
。這個關於動量算符表達式的修改也可以從位置-動量對易關係 (commutation relation) 的修改看出來。原來的對易關係是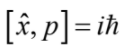 ,若要將i 改為-i,就必須同時將
,若要將i 改為-i,就必須同時將 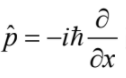 改為
改為 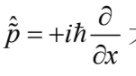 才是與原來的對易關係一致的結果。從以上這些討論可知,物理人與電機人對於複數表達式的不同使用習慣沒有誰對誰錯的問題,但必須在使用過程中搭配其它的相容習慣,且從頭到尾保持固定的使用習慣,不可任意改變,如此才不會得到矛盾的結果。
才是與原來的對易關係一致的結果。從以上這些討論可知,物理人與電機人對於複數表達式的不同使用習慣沒有誰對誰錯的問題,但必須在使用過程中搭配其它的相容習慣,且從頭到尾保持固定的使用習慣,不可任意改變,如此才不會得到矛盾的結果。
在結束這個主題之前,我們再問一個有趣的問題:既然古典物理也可以採用複數方法研究,那麼有可能寫出古典物理問題的 “薛丁格方程式” 嗎?對於這個問題,目前並沒有完整的答案,但可以舉一個具體的例子:一維諧振子 (harmonic oscillator) 。其運動方程式可以寫成以下兩式:
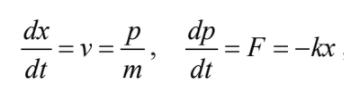 (8)
(8)其中m, k, v, F分別是質量、彈力常數、速度、回復力,而 x與 p分別是位置與動量。觀察可知 (8) 式可以改寫成矩陣形式:
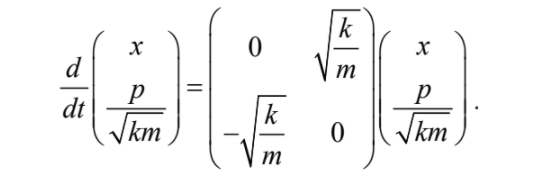 (9)
(9)定義態向量 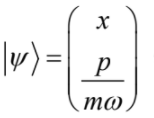 ,其中
,其中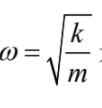 是諧振子的振動角頻率,並定義漢米爾頓算符 (Hamiltonian operator) 為
是諧振子的振動角頻率,並定義漢米爾頓算符 (Hamiltonian operator) 為 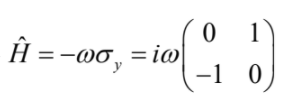 (這是一個厄米特矩陣 (Hermitian matrix),具有實數本徵值),其中
(這是一個厄米特矩陣 (Hermitian matrix),具有實數本徵值),其中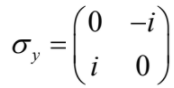 是對應 y 軸的包立矩陣 (Pauli matrix),並令普朗克常數 ћ=1(高能物理研究者常用的 “自然單位”!) ,則 (9) 式可寫成以下標準的 “薛丁格方程式”:
是對應 y 軸的包立矩陣 (Pauli matrix),並令普朗克常數 ћ=1(高能物理研究者常用的 “自然單位”!) ,則 (9) 式可寫成以下標準的 “薛丁格方程式”:
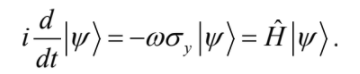 (10)
(10)
上述這個例子似乎模糊了古典力學與量子力學的界線,但這其實只是表面上的。畢竟對於像諧振子這樣的古典力學系統而言,上述的態向量並不具備機率相關的意義,而對系統的測量也不會導致 “波函數崩潰” 或是 “量子態躍遷”。
本文作者:欒丕綱