洗衣機物理學

我們因為現代家電的設計，省卻了許多生活上的勞務。偶而手洗幾件質料好的衣物，可能還蠻愜意的，但是如果少了洗衣機，日常的衣物通通都需要手洗的話，那麼大家的生活滿意度恐怕就得從「小姐」降成「丫鬟」了！
 

洗衣機的基本原理﹔離心力？向心力？

洗衣機的基本原理並不困難，主要是利用化學材料 (例如肥皂)，先把灰塵與油漬分解成較小的分子，讓它們溶解於水中，再利用洗衣槽的高速旋轉 (物理方法)，把溶有灰塵與油漬的汙水與衣服分離，藉此達到除塵去油的洗滌目的。
 

這個把水與衣物分離的原理，一般會很直覺地用「離心力」來解釋。然而，在物理的課堂上，正確的說法是：水與衣物纖維之間的摩擦力 (或附著力)，不足以提供水隨著衣物做高速旋轉所需的向心力，就像綁有細繩而做圓周運動的小石子，當細繩忽然斷裂，小石子因失去圓周運動所需的向心力，而朝著切線方向飛出去一樣，離開衣物的小水滴，也會透過洗衣槽上的眾多小孔，沿著轉動的切線方向飛出去。就「準備考試」而言，還請千萬記得，要避免使用「離心力」這個詞。
 

「直立式」與「滾筒式」，要選哪一種？

洗衣機算是家裡的中大型家電之一，售價不算便宜，買一台之後，能用上許多年。因此，相信大家在採購新的洗衣機之前，免不了要多方打聽、比較一下。面對市面上琳瑯滿目的洗衣機，大家是否會用上一些在高中物理課裡所學過的知識，來幫助判斷？
 

以全自動的「直立式」與「滾筒式」的洗衣機為例，不論個別的廠牌，單從基本物理力學的觀點來看，這兩種洗衣機都是靠圓周運動，一個在水平方向轉動、另一個在垂直方向轉動，你可曾想過，這樣的設計會導致什麼不同的洗衣效果呢？哪一種設計比較省水、省電？能洗得較乾淨，又不傷衣料？
 

這一期的專欄，我們分享一份十三年級 (高三) 的力學試卷，由紐西蘭物理學會所命題。如果你已經學過中學物理課裡的轉動、圓周運動與簡諧運動等概念，歡迎你拿出紙筆與計算機，給自己一點時間，來思考一下與滾筒式洗衣機相關的力學觀念。
 

試題一：洗衣機脫水、洗衣測試

小明任職於家電公司，手上的一項任務是設計洗衣機。他目前正在執行一些相關的測試。

滾筒式洗衣機的洗衣槽直徑 0.510 m，脫水時的轉速為每分鐘 1300 轉 (rpm)。測試時，兩疊衣物 B 與 C在洗衣槽的位置，如圖一所示。

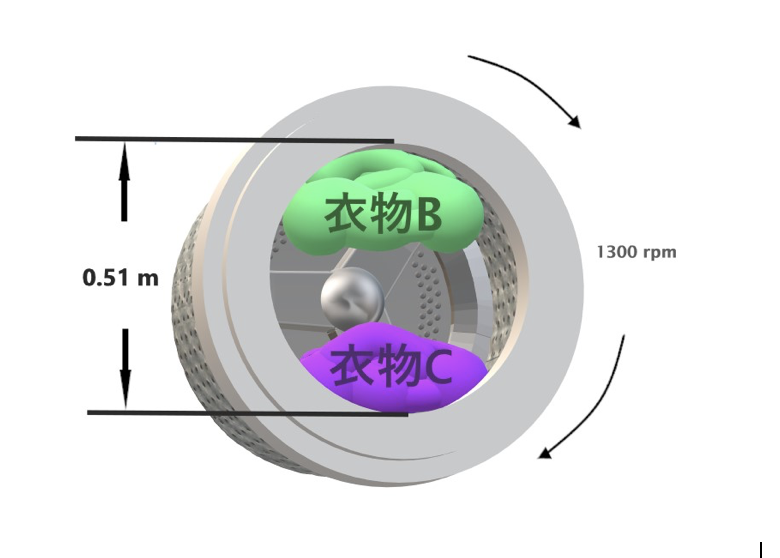
圖一

（a） 試證明緊貼在洗衣槽上的衣物，其最大速率為 34.7 ms^-1。

（b） 請以箭號分別標示作用於上方衣物B，與下方衣物C的所有作用力。

（c） 若B與C兩疊衣物的質量均為 0.400 kg。試計算位於上下這兩個位置的衣物，對洗衣槽的作用力大小為何？並註明作用力方向。

  d）小明希望了解洗衣槽尺寸對脫水效果的影響，選用了直徑加倍的洗衣槽來做研究。他讓兩台洗衣機的轉速相同，均為1300 rpm。試以相關的方程式，來討論這兩台尺寸不同的洗衣機，何者的脫水效果較好？

（e） 滾筒式洗衣機利用不斷地把洗衣槽內的衣物拋高、摔下，揉合了摔打、搓揉等手洗原理，來清洗衣物。為達到這個目的，洗衣槽的轉速不能太快，否則無法把隨洗衣槽轉到高處的衣物拋下。以直徑 0.5100 m的洗衣槽為例，試討論其最佳的轉速為何？並討論衣物在下拋過程中的運動軌跡。

註：洗衣槽的轉速可用每秒若干弳度 (rad s^-1) 或每分鐘若干轉 (rpm) 表示，須註明單位。
 

解答一：轉速與向心力

（a） 對轉動的物體而言，轉速與直線速度大小的關係式為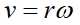。這道題的重點在於轉速的單位須為每秒若干弳度 (rad s^-1)，因此在把數值帶入公式之前，需要做一點單位換算，此外，題目所給的已知數是「直徑」，也考驗同學是否有細心閱讀試題：

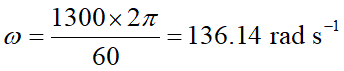
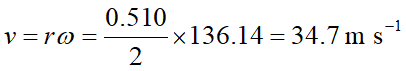
（b） 這道題的重點在於，學生應知道向心力是洗衣槽的正向力與重力二者的合力，而非單獨存在的一個真實的作用力。在鉛直面上作等速圓周運動的物體，向心力的大小是固定的，物體所受的重力大小也是固定的，但由於向心力的方向在頂點與底部的方向不同，所以洗衣槽對衣物的正向作用力大小會不同(如圖二所示)。

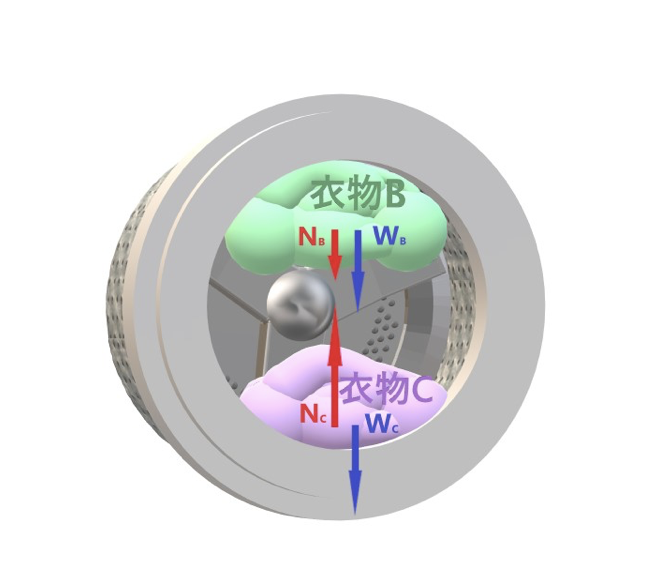
圖二：作用於衣物B正向力N_drum 與重力， 方向均朝下。作用於衣物C的重力方向朝下，但正向力N_drum  則朝上。

（c） 這是承繼上一題的定性觀念理解，進一步作定量計算。

衣物作等速圓周運動所需的向心力大小為

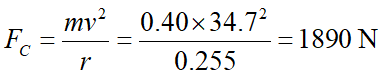
對上方的衣物 B 而言，它所需的向心力 (朝下) 是由洗衣槽的正向力 (N_drum   )與重力所提供：

                                                        Fc = (N_drum +mg)

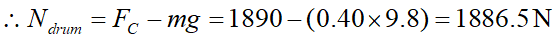
根據牛頓第三定律，此處衣物對洗衣槽的作用力方向是：朝上。

對下方的衣物 C 而言，它所需的向心力 (朝上) 是由洗衣槽的正向力 ( N_drum) 與重力所提供：

  Fc = (N_drum -mg)

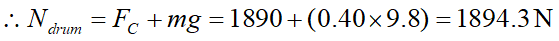
同理，此處衣物對洗衣槽的作用力方向是：朝下。

（d） 比較脫水效果，相當於比較向心力的大小。衣物在旋轉時所需要的向心力愈大，愈能使附著於衣物上的水滴與之分離。考慮離心力大小與半徑的關係：

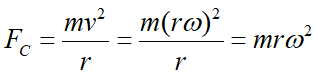
在轉速與衣物質量固定的情況下，離心力與半徑成正比，因此尺寸較大的洗衣槽，脫水效果也較好。

（e） 衣物不會從洗衣槽頂端滑落的最低速度是衣物與洗衣槽之間的正向力大小為零。亦即，衣物在頂端時，重力恰可提供轉動所需之向心力：

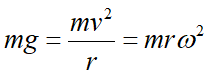
因此，最低轉速須為

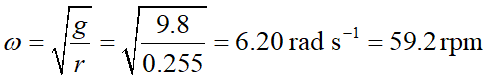
當洗衣槽轉速接近但低於6.20 rads^-1  (或59.2 rpm) 時，衣物會被帶至接近最高點的位置，然後因重力加速度大於旋轉所需的向心加速度，而與洗衣槽內壁分離，之後，則沿切線方向飛出，但由於重力加速度的影響仍在，所以，衣物會以斜向拋射的拋物線軌跡落下 (如圖三所示)。

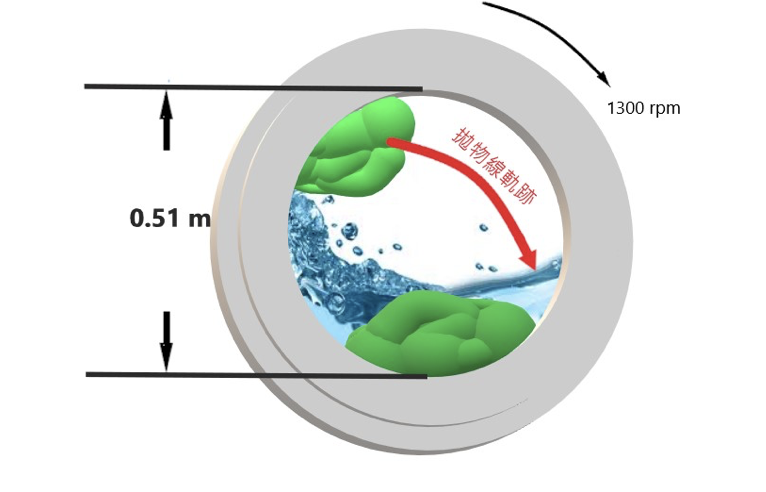
圖三：衣物會從接近高點的位置循拋物線軌跡落下。

然而，若轉速太低，衣物不會隨洗衣槽轉動而被拋起來，只會停在水槽的下半部，持續在肥皂水中浸泡，洗淨的效果不佳。因此，最佳轉速為略低於6.20 rads^-1  (或59.2 rpm)。

試題二：脫水後的減速測試

小明設計了一款新型的洗衣機，希望提升能源的效率。在脫水結束時，控制程式會切斷馬達的電源，使洗衣槽從轉速 1300 rpm 逐漸減速而停下來。讓洗衣槽煞車減速的原理，與發電機內將動能轉換為電能的原理 (冷次定律) 相同。

（a） 試證明洗衣槽的最高轉速為 136 rad s^-1。

（b）小明以空的洗衣槽做測試。空的洗衣槽轉動慣量為 0.155 kg m²，費時 140 s才從轉速 1300 rpm 靜止下來。試計算供應給煞車系統發電機的平均電功率為何？

（c）這款洗衣機另外配備了緊急煞車裝置，作用於軸心的煞車桿長 0.25 m，可施加211 N 的作用力。試計算當啟動緊急煞車裝置後，洗衣槽從極速 1300 rpm 到完全靜止，所轉動的圈數。

（d）洗衣機在脫水時，衣物會均勻的被向外擠到洗衣槽上，馬達會自動維持在固定的轉速轉動。假設衣物的質量沒有改變，試討論在脫水時，衣物從洗衣槽中央，到均勻的分布於在洗衣槽內側邊上的過程中 (圖四) ，馬達所消耗能量功率有何變化？
 

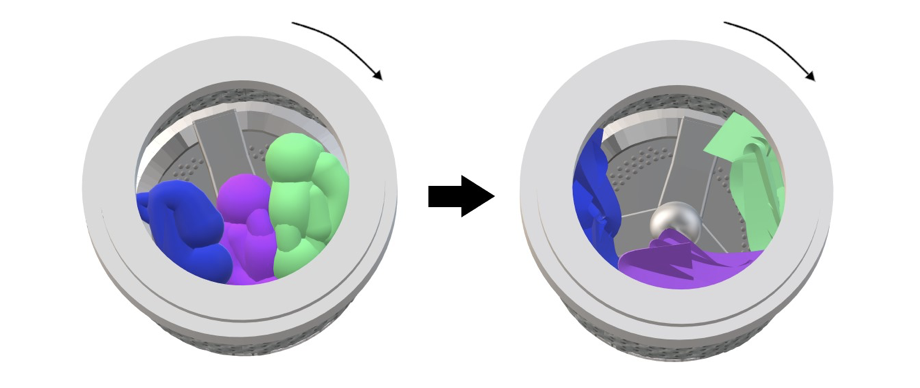
圖四

解答二：轉動運動學、力矩、轉動動能

（a） 這是簡單的單位換算問題：

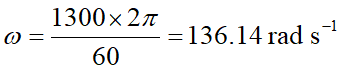
  b） 根據能量守恆的觀念，即使我們不知道具體的電路該如何連接 (如電磁感應、冷次定律等)，然而根據題目所給的已知數 (轉動慣量、轉速、時間)，我們仍可從「轉動動能」出發，來求得電功率大小：

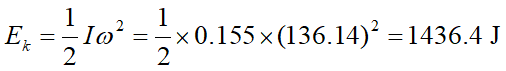
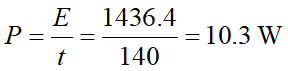
     （c）根據題意的煞車桿長、轉速變化 (應聯想到角加速度)，以及未知數為轉動的圈數，應該可以聯想到這是轉動的牛頓第二運動定律()。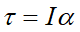

煞車桿對洗衣槽的力矩為 

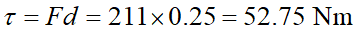
煞車力矩所產生的角加速度

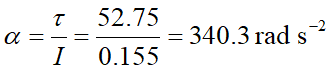
根據轉動運動學公式
   

洗衣槽在靜止前轉到的角度為

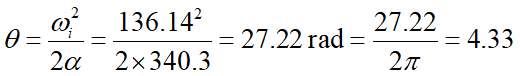 圈

 

（d）這道題的觀念在於轉動慣量的大小與質量的分布有關。當質量距離轉軸較遠時，系統的轉動慣量也較大。由於轉動物體的轉動動能為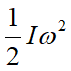，因此，當衣物平均分散在洗衣槽的外緣內壁時，洗衣槽的轉動慣量增加，需要較大的轉動動能，因而也會消耗較多的能量，亦即消耗較高的功率。
 

試題三：衣物不平衡時所引起的震動

洗衣機有兩個重要的組成，一個轉動的洗衣槽 (內桶) 外面，還有一個密不透水盛水槽 (外桶)，衣物透過洗衣槽的轉動，與外桶內的洗滌劑混合，達到清洗的效果。在箱體內部，外桶上方有兩根懸吊彈簧，下方有緩衝器，藉以減震 (圖五)。
 

圖五

小明在稍稍搖動未裝有任何衣物的洗衣機之後，注意到空的洗衣槽會自然地以 4.70 Hz的頻率來回振動。已知洗衣槽與懸吊彈簧的總質量為 23.4 kg。

（a） 試證明這兩個懸吊彈簧的等效彈性係數為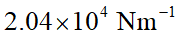
 。

（b）若有 6.0 kg 的衣物正在洗滌，這對洗衣槽的振動週期有何影響？

（c）當衣物分佈不均勻時，每次的轉動就等於是對洗衣槽的振盪系統提供一個外加的驅力。試以座標圖表示，在洗滌衣物時，洗衣槽的振幅如何隨著緩慢增快的轉速 (由 0 增到 10 Hz) 而變化，並在座標圖中以曲線表示阻尼緩衝器的效果。

（d）當洗衣機轉速達極速 1300 rpm 時，外殼上下振動的振幅為 0.60 mm。試問洗衣機上方的外殼，在振動時的最大加速度大小為何？並討論為何在脫水時，置於洗衣機上方的物體容易被抖落而掉到地面。
 

解答三：簡諧振盪、阻尼振盪、強迫振盪與共振

（a） 在計算等效彈性係數時，可以把懸吊彈簧與洗衣槽視為一條彈簧與一個質點的簡諧運動系統。把題目所給的頻率換算為週期，即可直接使用簡諧運動的週期公式:

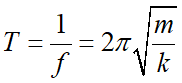
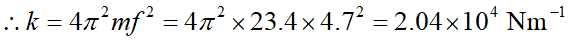
（b）洗衣槽沒有衣物時的振動週期為

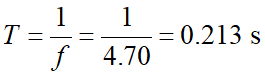
當洗衣槽內有 6.0 kg 的衣物時，新的振動週期為  

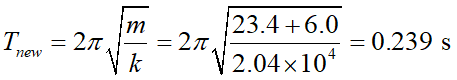
週期變化為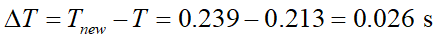 約不到百分之三秒。
 

（c）關於振盪現象，紐西蘭的高中物理介紹了簡諧振盪、阻尼振盪與強迫振盪，但後二者僅止於觀念上的定性介紹，並沒有涉及定量的數值計算。

簡諧振盪發生於物體在受有線性恢復力 (如彈簧) 作用的情況。若該系統還受有一個正比於物體運動速度的阻力，則稱為阻尼振盪。阻力愈大時，物體振盪的振幅也衰減得愈快。若在線性恢復力與阻力之外，還有一個周期性的驅動力時，則稱為強迫振盪。當外加驅動力的頻率等於物體振盪的自然頻率時，只需小小的驅動力，便能引發很大的振幅，稱為共振。

發生共振的條件為驅動頻率等於自然頻率 (在此為4.7 Hz)，在無阻尼的情形下，物體的振幅為無限大。在有阻尼的情況下，物體的振幅會減小；阻尼愈大，振幅愈小。繪圖重點在與振幅的峰值會出現在頻率5.0 Hz 附近，另再外加兩條峰值較小的曲線，來表示阻尼大小的影響，如圖六所示。(註：當阻尼增大時，其實會稍稍減小共振頻率，因此，函數圖型中的振幅峰值，除了減小之外，也會略為向左方偏移。)

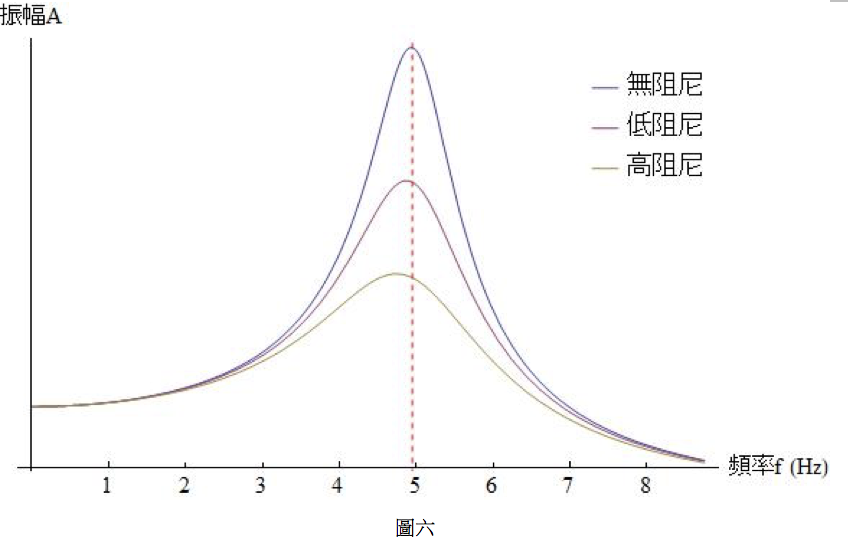
圖六

（d）我們知道簡諧振盪是一個變加速度運動，加速度的極大值會發生在端點處，以此洗衣機 (轉速 1300 rpm，振幅0.60 mm為例)：

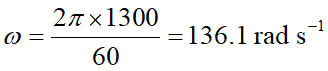
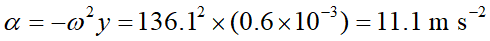
式中的負號表示加速度的方向與位移的方向相反。由於這個數值大於重力加速度 (9.8 ms^-2)，這表示在脫水時，由於振盪的緣故，洗衣機上方的平面會以大於重力加速度的加速度朝下運動，如此會與置於上方的物體短暫失去接觸，使得二者之間沒有摩擦力，因而可能抖落該物體。
 

結語

不知這幾道試題，是否讓你更能去思考一些洗衣機廣告文宣背後的涵義，以及有助於你去判斷這些文宣的虛實。例如：滾筒式採拍打、摔打方式進行洗滌，直立式利用水流讓衣物之間產生摩擦的方式來清洗衣物；滾筒式的洗淨效果較好、衣物較不易打結等等。

選購洗衣機當然不只是單純的物理問題，還得考慮經濟問題，例如預算有多少？家裡有多少人？多久洗一次衣服？若是白天工作繁忙，還得考慮夜間洗衣服時的噪音問題。此外，品牌、後續維修，是否需要定時或烘衣等功能？家裡的空間規劃，洗衣服需要蹲膝彎腰是否方便等等生活習慣上的問題。但相信，多了物理思考的加持，在決策上還是很有助益的。

此外，透過這台滾筒式洗衣機，不知道轉速 (rpm)、角速度 (rad s^-1)、力矩、角加速度、轉動慣量、振盪、共振、自然頻率等等這些物理名詞，有否變得更親切、具體一些？

現代的家庭用品，大多講求「人性設計」，只需幾個按鈕，就能完成很複雜的任務。本文的洗衣機就是一例。但也正是這些「人性設計」，加大了物理和我們之間的距離，而讓學生們覺得它是一門抽象難懂的學科。倘若我們能稍加還原一些現代家電背後的工作原理，就像拆解魔術師神奇的魔術那般，相信可以增添許多學習物理的趣味。