一切物質皆由基本粒子組成。粒子物理學是一門研究基本粒子相互作用的物理學分支。 從還原論角度看，粒子物理學是自然科學的基礎。在「粒子物理行」裏，我們會踏足粒子物理學的每個角落，包括粒子物理的基本概念、主要研究成果和一些有關歷史。
 

粒子

在介紹基本粒子之前，先讓我們了解粒子是甚麼。要說清粒子是甚麼其實並不容易。現代 物理學對粒子的描述涉及到量子力學和狹義相對論，與我們直覺中的「經典粒子」有點 不同(「經典」(classical)一詞泛指任何非量子概念)。我們一般會認為，粒子是一個很小的顆粒，它在每一時刻有其確定的位置。但量子力學告訴我們,粒子的位置並不確定。粒子是一個波包(wave packet)(圖一)。
 

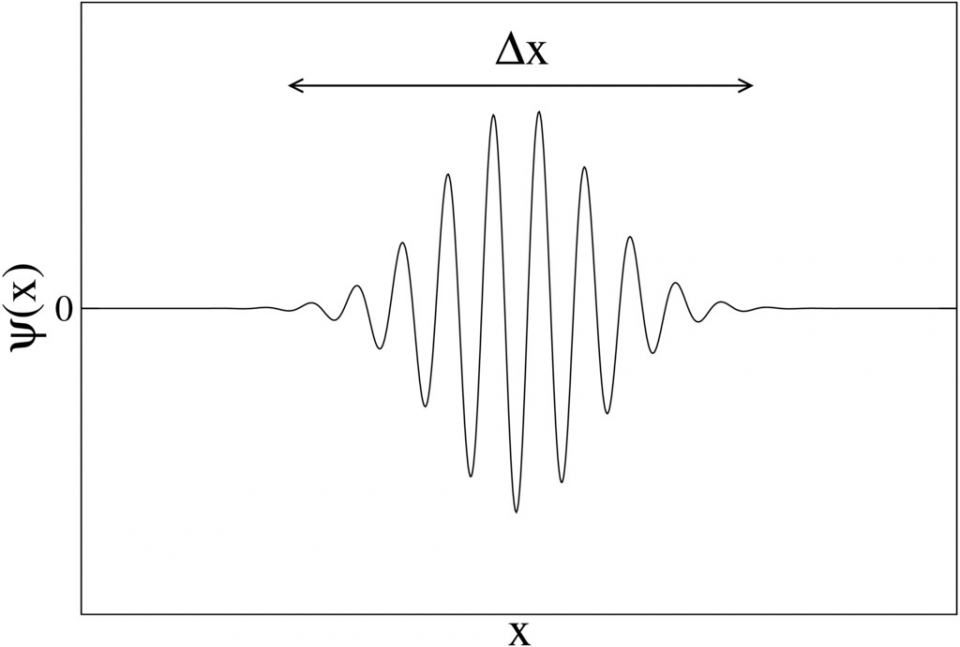
如圖所示，波包基本上被限制在長Δx的區域，雖然該區域之外也有很小的非零值。也就是說，如果Δx很小，我們便以為粒子的位置很確定。事實上，Δx的確很小，但並不為零。圖二是對電子進行的雙縫實驗：電子(顯示為波) 一顆一顆地被射向一個間距約為1μm的雙縫，投射在屏幕的電子會留下一個點狀印記。

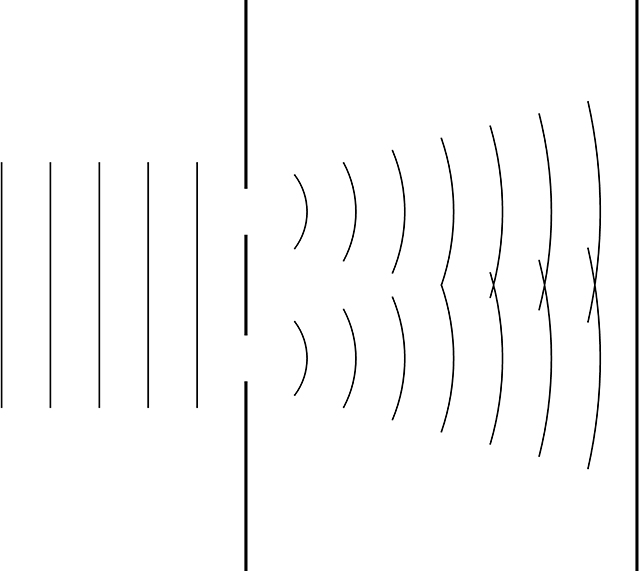
圖三是實驗中的點狀印記分佈結果。圖a為實驗剛開始不久的印記分佈。可見電子彷彿無序的隨機散落在屏幕上。圖b、c、d和e為隨着時間過去，落在屏幕上的電子數目愈來愈多的結果。點狀印記的多條紋分佈是干涉現象，印記集中處為建設性干涉(constructive interference)，這證明Δx不為零，即電子同時穿過兩個縫。如果Δx為零，即電子具有確定位置，那麼它只能穿過其中一個縫，從而印記分佈應如圖四。Δx非零說明電子是波，Δx很小說明電子是粒子，這就是波粒二象性。 

圖三  （A. Tonomura et al. (1989)）

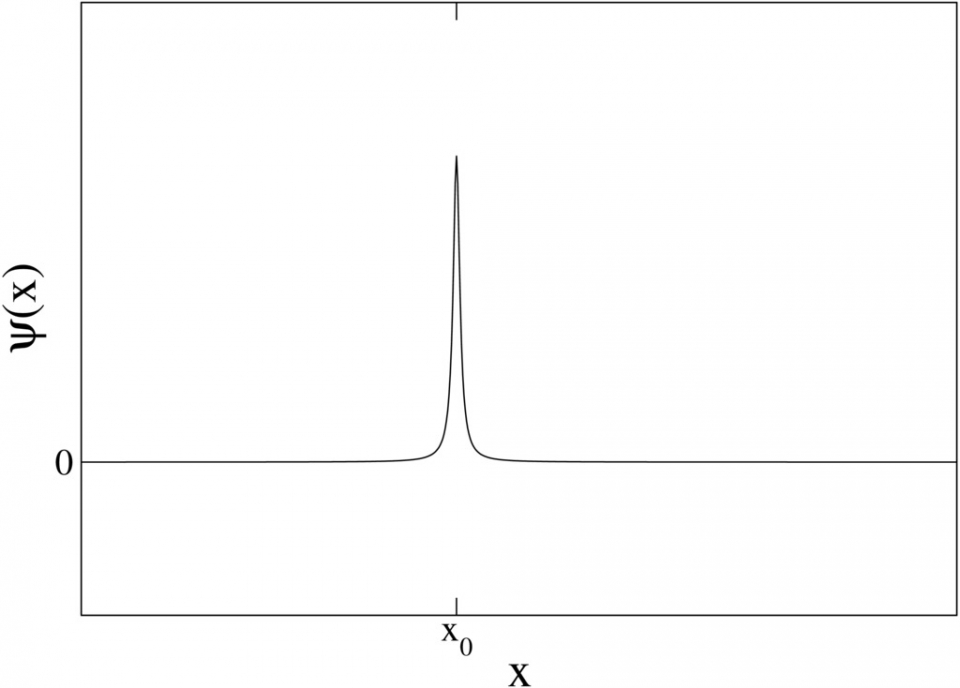
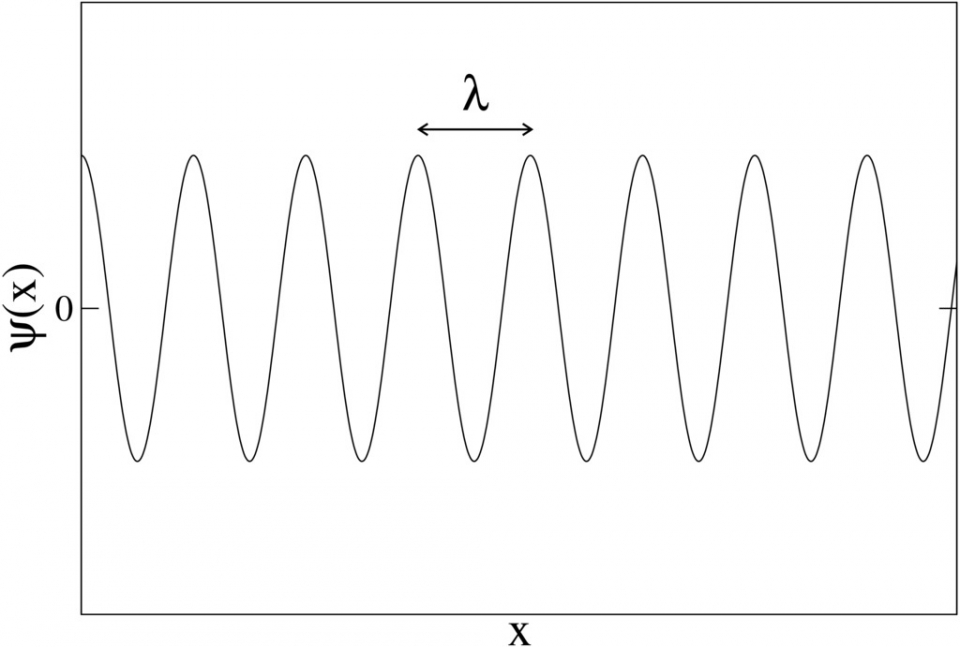
所以，每個粒子由一波函數ψ(x)來描述(例如,波包的波函數如圖一)，其中x為位置。波函數包含了一切關於該粒子的訊息。例如，波函數的平方|ψ(x)|²正比於粒子在位置x出現的機率。原則上，該粒子的任意可觀察量(observable)(如能量、動量、角動量等)被量度時所取的值的機率皆可從波函數獲得。給定可觀察量A，只有呈特定分佈的波函數可以有確定的A值。這些有確定A值的波函數稱為可觀察量A的本徵態(eigenstate)。例如,具有確定位置x=x₀的波函數是一個位於x₀，寛度為零的峰(圖五);而具有確定動量p的波函數是一波長為λ=h/p(其中h為普朗克常數(Planck constant))的正弦波(圖六)。注意！圖五極不像一個正弦波，所以當位置確定時動量極不確定。類似地，圖六的正弦波伸延到無限遠，所以當動量確定時位置極不確定。更量化地說，位置的不確定度和動量的不確定度成反比(這裏不確定度指統計學上的標準差):

這就是測不準原理(uncertainty principle)。在現代量子力學的框架裏，測不準原理並不是基本原理，它可以由量子力學的基本原理導出。

圖五


圖六

原則上，位置的不確定度Δx是可以任意大的。如圖二中，細小的波包(Δx很小)穿過雙縫後變成兩個交疊着的扇形波。這兩個波會不斷擴散(Δx增大)，直至它們到達屏幕，與屏幕上的原子發生相互作用。可是，由於電子與屏幕上的原子間的相互作用具有局域性 (locality)，即相互作用發生在一個很細的區域裏,相互作用的結果是一個某位置上的細小印記(電子撞上原子，放出光子，形成螢光點)。換句話說，電子位置的訊息透過與宏觀系統的相互作用被確定並且放大。這種微觀系統的訊息因與宏觀系統相互作用被確定並放大 的過程便是量度(measurement)。當電子碰上屏幕，形成印記，它的位置便被確定下來，波函數瞬間由位置不確定的交疊扇形波變成位置頗確定的細小波包(圖一)。這種波函數的突變過程稱為量子態塌縮(wavefunction collapse)。一般情況下，電子頻密地與宏觀環境進行相互作用，所以量子態頻頻塌縮，導致Δx沒有充份時間擴大至宏觀尺度，而絕大部份時間維持在細小波包狀態。這就是為什麼在宏觀尺度下電子的位置彷彿很確定。即使在圖二的電子雙縫干涉實驗裏,雙縫與屏幕的距離並不大,為約10μm，而屏幕上的干涉條紋間距僅為約1μm。量子態的塌縮機制涉及到量子系統與宏觀環境的量子糾纏(quantum entanglement), 並且有些方面在學術界仍未有定論，是一個物理學的未解決問題，稱為量度問題(measurement problem)。我們不會對此課題作深入探討。以上對量度的看法只是其 中一派學說，稱為環境誘導超選擇(environment-induced superselection，簡稱einselection)。

粒子的波函數會隨時間而演化，演化的過程必須使得粒子被發現的概率在每一時刻均為 1，這種演化稱為麼正演化(unitary evolution)。主宰波函數麼正演化的方程稱為薛丁格方程(Schrödinger equation)。我們不會詳細探討薛丁格方程，我們只須明白演化的麼正性，即發現概率常為1。量子力學的麼正性將在粒子物理裏扮演着重要角色。 

場

光是電磁波，即電磁場的振動在空間的傳播。在由馬克士威方程(Maxwell equations)主宰的經典電動力學裏，電磁場具有空間分佈，即是波。粒子間的電磁相互作用透過電磁場來傳遞。例如，兩電子間的靜電斥力由它們所產生的電場傳遞。電磁埸有如物質，具有能量，動量和質量。例如，兩個電子之所以互相排斥，是因為它們所產生的電場能量隨它們距離增加而減少。而電子本身的質量有一部份便是來自它產生的電場。所以，在經典物理學裏，物質分為兩類：一類是如電子和原子等的粒子，另一類是如電磁場的場，是一種波。

從以上對粒子的討論中，我們知道電子和原子等粒子具有波的性質。從極微弱雷射的雙縫實驗中，我們也可獲得類似圖三的結果。這說明光不但具有波的性質(干涉現象),也具有粒子性質(屏幕上的點狀印記)。所以，量子力學中的波粒二象性統一了粒子和場這兩個經典物理學概念。

當然，正如電子，光子(組成電磁場的粒子)在絕大多數情況下以小波包(圖一)的狀態出現。可是，光的干涉現象在日常生活中並不難看見(例如路面油漬上的彩色圖案便是一干涉現象)，而電子或原子的干涉現象幾乎不可能在日常生活遇到。這是因為可見光的波長遠遠大於一般電子或原子的波長(可見光的波長約為1μm，而室温下的氫份子(H₂)波長約為 10^-10m)。圖七顯示了波長小的波穿過雙縫時的情況，可見幾乎沒有任何干涉(兩波重疊時因疊加而導致的消長)或繞射現象(波經過缺口後的縱向擴散)。

圖六

量子場

以上我們從量子力學的角度統一了粒子和場的概念。我們並未考慮到現代物理學的另一基石—相對論。在經典物理學裏，狹義相對論修正了牛頓力學，給出了粒子在高速時的正確行為(如時間延長、長度縮短、相對論性速度疊加等)，也給出了著名的質能等價關係 E=mc²(其中E為質心系中的系統總能量，m為系統總質量，c為光速)。在量子物理學裏，狹義相對論蘊含着眾多翻天覆地的驚人結論。這些驚人結論比時間延長、質能等價等更荒誕離奇，但都一一被實驗證實。基於量子力學和狹義相對論的粒子理論稱為量子場論。量子場論的成功可說是量子力學和狹義相對論的最佳鐵証。還有，量子場論具有環環相扣的緊密邏輯結構，只要理論架構的一小塊被拿掉，整個理論便會因內在不相容而塌陷。因此，量子場論可說是大自然的完美藝術品，而人類有幸能發現它，一窺它的奧秘，本身就是一個值得讚嘆的奇蹟。

在本章裏，我們會對量子場的概念作初步了解。在未來的章節裏，我們會一一探討量子場論的精密邏輯結構、驚人結論和實驗驗證。值得注意的是，至今物理學家對如何把量子力學和廣義相對論結合仍然未有定論，有機會我們也會對這課題作一窺探。

在牛頓力學中，各自粒子的質量為守恆量，隨時間不變。也就是說，粒子不可能變成其他質量不同的粒子。在狹義相對論中，質能等價關係預言了只要總能量和總動量守恒，粒子可以被湮滅，轉化成其他粒子。例如，電子和反電子相遇時有可能互相湮滅，變成兩顆質量為零的光子。又例如，光子可以因被原子吸收而消失(這就是為何物質會有顏色!)。所 以，對於給定粒子的種類，該種粒子的粒子數並不守恆，隨時間而變化。假定粒子的種類為光子。那麼,要描述光子所組成的場(電磁場)的量子態，我們當然要知道光子的波函數。可是由於光子數量是不定的,我們必須知道有一顆光子的波函數、有兩顆光子的波函 數、有三顆光子的波函數，如此類推。也就是說，場的量子態由以下一系列波函數描述：ψ₁(x₁),ψ₂(x₁,x₂),ψ₃(x₁,x₂,x₃),... 。這一系列波函數可簡寫成{ψ_n(x₁,...,x_n)}。所以，我們說{ψ_n(x₁,...,x_n)}描述了電磁量子場的態。這裏我們使用了多粒子波函數ψ_n(x₁,...,x_n)的概念。這概念不難理解。例如，ψ₂(x₁,x₂) 的平方|ψ₂(x₁,x₂)|²正比於一顆光子在x₁並且另一顆光子在x₂的概率。

所以，量子場其實就是把場視為某種粒子的集體，而粒子有其波函數，並且粒子數並不確定。換句話說，每種粒子都對應一個量子場。例如光子對應電磁場，而電子對應電子場。從這種角度看，粒子是量子場的激發。這就解釋了為何每顆電子都有相同的質量和電荷，因為它們是同一個場—電子場—的激發!

我們之前提及過波函數演化的麼正性,它保證粒子被發現的機率總為1。可是，正如以上提到，粒子是可以被湮滅的。所以，在量子場論裏，麼正性只要求量子態在被量度時所獲得不同量度結果的概率總和為1。例如，如果初態為一顆電子和一顆反電子，那麼終態被量度時可以是兩顆光子、三顆光子、正反電子加一顆光子，如此類推。而這些不同的量度結果的概率總和必須為1。

以上我們也提及過粒子相互作用的局域性(locality)。粒子相互作用的局域性是粒子之所以稱為粒子的原因。而量子場論便是一遵從局域性的粒子理論。在一些現代粒子理論的延伸中，例如弦論(string theory)，物質的基本單元不是零維度的粒子，而是一維的弦。弦的長度是可變的，在高能振動下可以變得很長。所以弦與弦之間的相互作用並不具有局域性。可是，由於弦本身有張力，當振動能量很低時，它的長度很短，像一顆粒子。所以，弦論在低能現象中與量子場論無異。 



延伸閱讀：

粒子物理行（二） 粒子的分類和對稱原理