
粒子物理行(二) 粒子的分類和對稱原理
- 粒子物理行
- 撰文者:黎偉健
- 發文日期:2018-03-06
- 點閱次數:4018
 粒子的分類和對稱原理
粒子的分類和對稱原理
在第一章裏,我們對量子場作了初步了解。由本章開始,我們會嘗試了解量子場論的基本架構。
在第一章裏,我們明白到每一種粒子都對應一量子場,而粒子是量子場的激發。一個很自然的問題是:給定兩顆粒子,怎麼辨別它們是否同一種粒子? 也就是說,給定兩顆粒子,怎麼辨別它們是否同一個量子場的激發?例如,為什麼我們說電子和光子是不同的粒子?要回答這個問題,我們必先了解量子埸論的一個基本原理(也可能是最重要的一個原理)—對稱原理(symmetry principle )。簡單來說,對稱原理意思是粒子間的相互作用取決於物理定律的對稱性。而粒子的分類其實就是粒子的相互作用行為的分類,所以物理定律的對稱性在粒子的分類裏起着關鍵性作用。在以下的討論中,我們將考慮最一般意義下的粒子。也就是說,粒子不一定是如電子般的基本粒子,也可以是如質子甚至氫原子般由數顆基本粒子組成的合成粒子。
在第一章裏,我們知道粒子的量子態由它的波函數ψ(x)來描述。注意ψ (x )在是波函數ψ在位置x的值,也可視為量子態|ψ〉的x分量,記為〈x|ψ〉= ψ (x)。而我們也知道,給定可觀 察量(observable)A,某些量子態具有確定的A值,稱為A的本徵態,記為 |a〉,其中a為 量度A時所得的確定值,稱為本徵值。設想給定一顆自由粒子,如果在任何時刻量度可觀 察量A, B, C,… 時(不論時序或次數),都得到確定的值a, b, c, …(也就是說,該粒子的 量子態是A, B, C,…的共同本徵態 |a, b, c,...〉,a, b, c, … 稱為量子數(quantum number)),那麼很自然地我們可以用a, b, c, … 來標籤該粒子。這組可以同時被精確量 度的可觀察量A, B, C,… 稱為相容可觀察量(compatible observables)。而且,由於這些 a, b, c, … 的值不隨時間變化,A, B, C,…是守恆量。所以,要知道怎樣把粒子分類,我們必先知道哪些可觀察量是彼此相容的守恆量。
 對稱性和守恆量
對稱性和守恆量
相信每一個接觸過科學的人都知道能量守恆定律—孤立系統的總能量不隨時間變化。可是,什麼是能量? 為什麼能量守恆? 這些都不是容易解答的問題。 例如,一個蘋果從樹上掉下,它的速度增加,引力勢能轉化成蘋果的動能。當蘋果碰到地面,停了下來,蘋果的動能轉化成地面和空氣分子的動能,所以有聲響產生,而且地面温度輕微上升。地面温度上升會順帶發放更多熱輻射(室温下主要是紅外線)。熱輻射是電磁場,也帶有能量。所以,無論是引力場、分子還是電磁場,它們都具有一物理量,稱為能量,而能量的總和不隨時間變化。想深一層,這是一個非常奇妙的現象:引力場、ㄈ 子和電磁場是截然不同的物質形式,為什麼它們好像密謀着什麼,非要能量守恆不可? 在理論物理裏,我們可以從電磁場的值嚴格計算電磁場所儲存的能量;我們也可以從分子的質量和速度計算它的動能。物理學家當然不會滿足於怎樣計算能量,他們要了解為什麼宇宙間有如此普遍的定律—能量守恆定律。
從現代物理學的角度,能量守恆是基於物理定律的時間平移對稱。對稱性即變換下的不變 性。物理定律的時間平移對稱,意思是同一套物理定律在不同時刻一樣適用,即宇宙中沒 有特殊時刻。例如牛頓的萬有引力定律,無論是三百年前還是現在都適用。把能量守恆歸 究為“理所當然”的時間平移對稱,可以說是對能量守恆的完美解釋。這種守恆量與對稱性 的關係是一普遍定理:每種物理定律的對稱性都對應一守恆量。這定理稱為諾特定理 (Noether's theorem)。隨了時間平移對稱,還有哪些對稱是“理所當然”的呢? 很自然,在 台北的物理定律應該與在香港的物理定律相同,也應該與在火星的物理定律相同,即宇宙中沒有特殊位置。這是空間平移對稱,其對應的守恆量是動量。類似地,宇宙中沒有特殊方向,這是空間旋轉對稱,其對應的守恆量是角動量。還有,宇宙中沒有特殊速度,這 是均速參考系變換對稱,其對應的守恒量稱為K。對於自由粒子,K = tp− Ex(其中t為時間,x為位置,p為動量,E為能量,這裏我們把光速c定為1)。由於自由粒子的p和E守恆,K守恆的結論是p = Ev,其中v為粒子速度。對狹義相對論有點認識的讀者應該不會對此關係式感到陌生,但有趣的是此關係式也源自於對稱性。
 龐加萊羣、質量和自旋
龐加萊羣、質量和自旋
描述對稱性的數學是羣論(group theory)。羣論研究對稱變換的性質,並把對稱性分類,在粒子物理學裏是極為重要的數學工具。一個羣就是一組對稱變換,並且任意兩個變 換可以結合成另一個變換。例如沿z軸的旋轉,旋轉了角度θ1後再轉動角度θ2,便可獲得 一個角度為θ1+ θ2的旋轉。所以沿z軸的旋轉構成了一個羣,記為SO(2)。值得注意的是,羣論研究的是羣的結構,所以並不在乎受對稱變換作用的對像是什麼。例如,由於 SO(2)的元素(即沿z軸的旋轉)可以用旋轉角度θ表示,而θ取值範圍為0 ≤ θ < 2π,並且 旋轉θ = 2 π與旋轉θ = 0無異,所以我們可以把SO(2)視為連續的實數綫段[0; 2π],其中0 和2π 被視為同一點,而任意兩個元素的結合就是綫段上的實數加法。從這個簡單例 子,我們看到了羣不但有其代數結構【註解1】,也有其拓撲結構【註解2】(例如SO(2) 的拓撲結構與一維圓圈無異)。羣的這些有趣性質在粒子物理裏有很多重要應用,以後我 們有機會會遇到。類似SO(2),描述連續對稱的羣稱為李羣(Lie group)。
符合狹義相對論的時空對稱組成了龐加萊羣(Poincaré group)。龐加萊羣是一個李 羣。以上所提及到的物理定律的對稱性(時間平移對稱、空間平移對稱、空間旋轉對稱和 均速參考系變換對稱)涉及到時空座標的平移和旋轉,屬於連續時空對稱,因為平移的距 離和旋轉的角度可以取連續實數值。連續時空對稱組成了龐加萊羣的一個子羣【註解 3】,稱為正規龐加萊羣(proper Poincaré group)。至今,所有已知物理定律均不依賴於 時間、位置、方向和參考系速度,而且所有實驗結果均符合能量守恆定律、動量守恆定 律、角動量守恆定律和K守恆定律(p = Ev)。因此量子場論的基本假設是物理定律嚴 格遵守連續時空對稱。
考慮一自由粒子。很自然地,我們不會認為時空平移、空間旋轉或均速參考系變換會改變粒子的種類(當然,這純粹是一符合直觀的約定俗成)。那麼,標籖粒子種類的物理量必須在連績時空對稱變換下保持不變。可以從數學上證明,在連續時空對稱變換下保持不變的時空物理量只有兩個:粒子的質量m和自旋s。(這裏時空物理量指如位置、動量和能量等與粒子運動有關的物理量。非時空物理量的一例子是電荷。)這是正規龐加萊羣的一個重要結果。
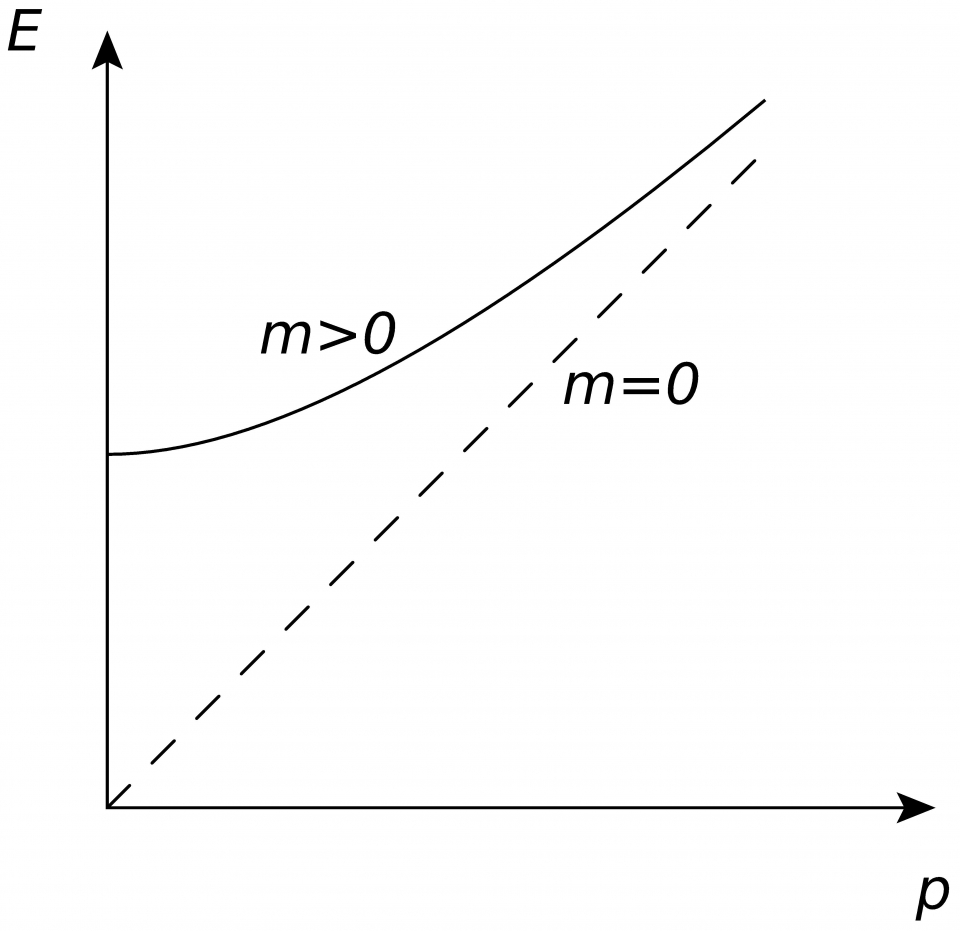
粒子的質量m是粒子的運動慣性。m與能量E和動量大小p有以下關係:m2 = E2 −p2。 也就是說,給定質量m,能量E和動量大小p的關係是一雙曲線(m = 0是特例,對應
E = p,即能量正比於動量),稱為質量殼(mass shell)(見圖一)。正如時間和位置座 標(t, x, y, z)組成了四維時空,(E, px, py, pz)組成了四維動量空間。所以,質量殼方程描述了四維動量空間中的一個三維曲面。粒子的質量可最0或以上任何實數值。
自旋s是自旋向量S的模長(嚴格來說,S2 = s(s + 1) (h/2π)2 ,其中h為普朗克常數)。自旋向量S是粒子在其靜止參考系中的角動量。有趣的是,我們無法從經典物理學角度了解粒 子的自旋。例如,如果把電子的自旋角動量歸究為電子作為一球體的旋轉,那麼,由於 電子的體積極小,球體表面的速度必須超過光速,但這違反狹義相對論。還有,與質量 不同,粒子的自旋s取離散值0,1/2, 1, 3/2, 2,… 。這是因為時空平移的大小可取任意實數 值,所以時空平移組成的羣是所謂的非緊緻李羣,對應的不變量(質量)可以取連續值。 而粒子的靜止參考系中的空間旋轉角度只能取0至2π,並且0和2π被同等起來,所以這 些空間旋轉組成的羣是所謂的緊緻李羣,對應的不變量(自旋)只能取離散值。這是李羣表示(representation theory)的重要結果。當然,我們不會詳細探討李羣的數學。可是,從這個例子,我們已經能體會到抽象的現代數學理論對粒子物理學的重要性。
隨了連續的時空對稱,還有離散的時空對稱,而這兩種對稱組成了整個龐加萊羣。離散時 空對稱只有兩個:宇稱和時間反演。宇稱變換即空間座標反演
(x→-x, y →-y, z→-z),而時間反演即時間座標反演(t →-t)。實驗證明,物理定 律並不遵從這兩種離散時空對稱(這現象稱為對稱破缺),即宇宙中有左右之分,並且時 間流逝有往前和往後之分。我們會在未來的章節詳細討論離散時空對稱和它們的破缺。 在本章,我們會忽略離散時空對稱。
 相容可觀察量
相容可觀察量
在量子力學裏,有嚴格的數學方法判斷兩個可觀察量A、B是否相容。如果A是守恆量, 那麼我們可以用以下一簡單規則判斷A和B是否相容:如果B在A所對應的對稱變換下保 持不變,那麼A和B便是相容的可觀察量,反之亦然。例如,動量的x分量px,它對應的對稱變換是x方向的平移。x座標當然在x方向的平移下會改變,所以x和px不相容,不能 同時被精確量度,即第一章所提及到的測不準原理。我們也可考慮y座標,它在x方向的平移下保持不變,所以y和px相容。
考慮一自由粒子,讓我們嘗試列舉所有彼此相容並且守恆的時空物理量。以上我們已知道 粒子的質量和自旋在連續時空對稱變換下不變,所以它們與其他守恆時空物理量相容。設 該粒子的動量為p,那麼沿p方向的空間旋轉並不改變p(見圖二),所以這空間旋轉對應的守恆量—角動量沿動量方向的分量—與p相容。
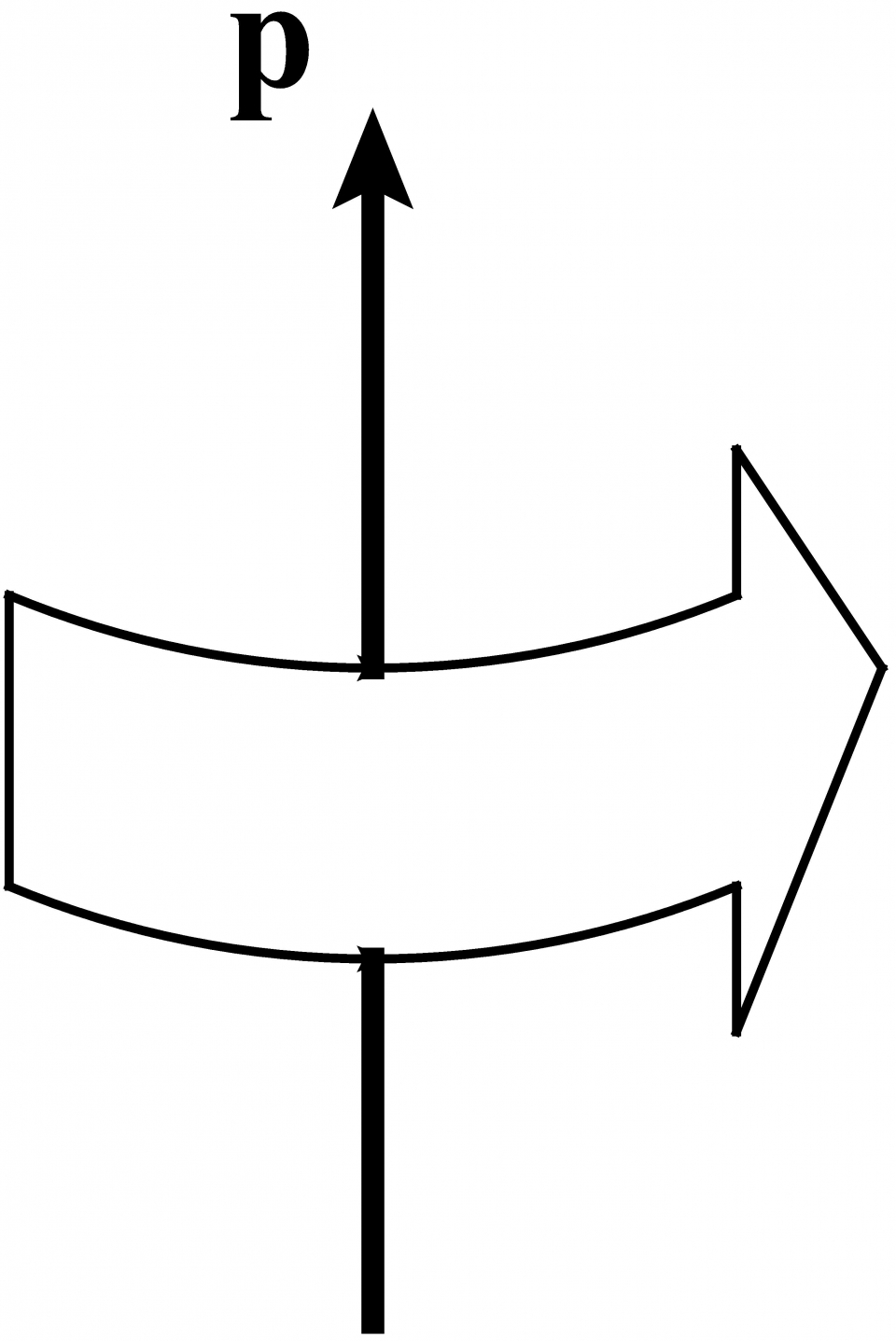
角動量J沿動量方向的分量J·p/|p|稱為螺旋度(helicity),記為σ。所以,動量p、螺旋度σ、質量m和自旋s是互相獨立,彼此相容的守恆時空物理量。可以證明,這四個物理量是具有該性質的最大組合。因此,一顆粒子的量子態可以用這四個物理量來標籤:
|p, σ, m, s〉
注意,m和s標籤粒子種類。給定粒子種類,粒子的動量向量可取任意值。螺旋度σ取離散值。如果m>0,σ可取以下值(以h/2π為單位):–s, –s+1, …, s–1, s。如果m=0,σ只能取以下值:–s, s 。值得注意的是,對於m = 0,粒子必須以光速運動,所以並不存 在粒子的靜止參考系。所以,零質量粒子的自旋s應理解為螺旋度σ的絕對值。而且, 對於零質量粒子,螺旋度在任何連續時空對稱變換下保持不變。所以,嚴格來說,對於 m = 0,σ = s和σ = –s對應兩種不同種類的粒子!我們會在未來看到宇稱變換聯繫着這 兩種粒子。還有,零質量粒子的自旋之所以取離散值,並不是因為旋轉羣的緊緻性,而是因為龐加萊羣並非單連通拓撲空間。非單連通的意思是並非每一條閉合曲線都能收縮成 一點,甜甜圈便是一例子。從此例,我們看到對稱羣的拓撲結構與粒子的特性有着微妙的 關係。零質量粒子的一例是光子。光子的自旋s為1,所以螺旋度σ可取值1或–1,這分別 對應光的右旋偏振態(圖三a)和左旋偏振態(圖三b)。

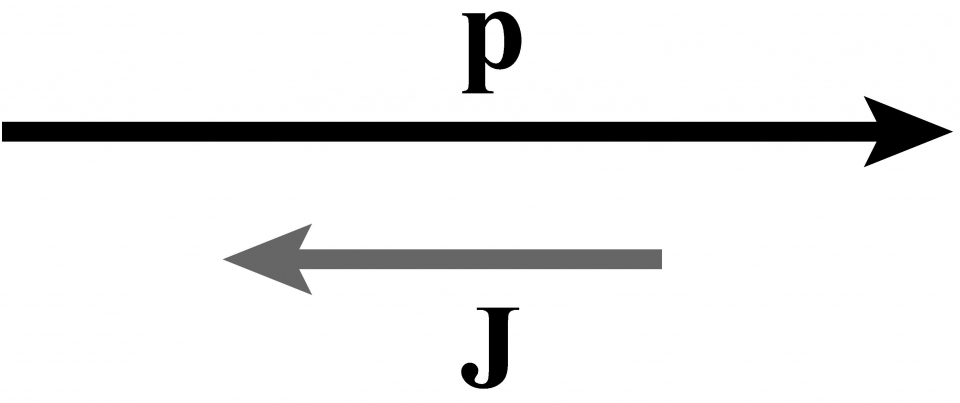
圖3(a) 圖3(b)
 內在對稱和超對稱
內在對稱和超對稱
以上,我們考慮了時空對稱和它所導致的粒子分類。更一般地,我們可考慮任意對稱, 包括非時空對稱。內在對稱(internal symmetry)是不涉及任何時空變換的對稱。內在對稱的最簡單例子是U(1)EM規範對稱(gauge symmetry),它對應的守恆量是電荷。規範對稱這概念有點抽象。簡單來說,粒子對應的場在每一時空點都有一數值(當然,因為量 子力學中的不確定性,這數值遵從一機率分佈【註解4】)。這一數值的取值範圍便是內 在空間。場的這一數值可被視為內在空間中的一個向量,而規範對稱便是內在空間的旋轉 對稱。我們在將來會對量子場論中各式各樣的內在對稱作詳細探討。這些內在對稱包括電 荷共軛對稱(charge conjugation symmetry)、SU(3)c規範對稱、SU(2)W 規範對稱等。 還有一種對稱,它是時空對稱和內在對稱的混合,稱為超對稱(supersymmetry)。時 空對稱、內在對稱和超對稱窮盡了量子埸論中所有可能的對稱性。超對稱到目前為止並 未被實驗證實。在本章,我們將不會考慮超對稱。
根據諾特定理,每種內在對稱都對應一守恆量,稱為荷(charge)。電荷便是一種荷。由 於荷是一內在物理量,它在時空對稱變換下不變,因而與守恆時空物理量相容。考慮彼此 獨立並且相容的荷的全體,把它們的本徵值記為n (n可以代表多個量子數,電荷為其中之 一)。那麼,一自由粒子的量子態可以寫成
|p, σ, m, s, n〉
也就是說,粒子的種類由質量m、自旋s和荷n標籤。給定了m、s和n,粒子仍可有不同的動量p和螺旋度σ。可是,這些取不同的p值和σ值的態互相由連續時空對稱變換(如均速 參考系變換和空間旋轉)聯繫着(正如以上提到,零質量粒子是特例,對於它們,σ也是標籤粒子種類的一個量)。我們稱一組互相由一個羣聯繫着的態為該羣的一個不可約表示 (irreducible representation)。也就是說,所謂一種粒子,其實就是正規龐加萊羣的一個 不可約表示,而每一個不可約表示以m、s和n來標籤。
 一些歷史
一些歷史
埃米·諾特(Emmy Noether, 1882-1935)出生於德國南部城市埃爾朗根的一個猶太知識份 子家庭,父親也是數學家,在埃爾朗根大學任教。諾特於1907年在不變量理論大師哥爾丹 (Paul Gordan)的指導下於埃爾朗根大學獲得博士學位。可是,儘管諾特才華横溢, 由於當年女性基本上不可能獲聘學術研究職位,她在埃爾朗根數學研究所無薪工作了七 年。1915年,因為諾特在不變量理論的專長有助了解廣義相對論,希爾伯特(David Hilbert)和克萊因(Felix Klein)邀請她到哥廷根大學任教。但因為語文學者和歷史學者 的反對,諾特在希爾伯特名下無薪任教了四年,於1919年才正式獲得教學資格。1933 年,納粹執政,禁止猶太人在德國大學任教,諾特因此移居到美國,在布林莫爾學院 (一所女性文理學院)任教。1935年,諾特患上卵巢囊腫,於手術後四天不幸離世,享年 53歲。諾特是抽象代數的研究先驅,在環理想理論和非交換代數作出了非凡供獻。在理 論物理裏,她於1915年證明的諾特定理,給出了物理定律的對稱性和守恆量的關係,是 現代理論物理學的基石。愛因斯坦和外爾(Hermann Weyl)更認為諾特是數學史上最重 要的女性。隨了卓越的研究成就,諾特也很提攜後輩,經常與學生討論數學,甚至不介 意學生以她尚未發表的新概念出版論文。她的很多學生後來都成為了知名數學家。

埃米·諾特 (圖片來源:Wikimedia commons)
尤金·維格納(Eugene Wigner, 1902-1995)是量子力學中對稱原理的奠基者。維格納生於 匈牙利布達佩斯的一個猶太中產家庭,父親是皮革制革商人。維格納在柏林工業大學攻讀 化學工程,之後在柏林的德皇威廉學院完成博士學位,論文題目為《份子的形成和衰 變》。之後,他主力鑽研量子力學和羣論。1927年,他被索末菲(Arnold Sommerfeld) 邀請到哥廷根大學作為希爾伯特的助手。但由於希爾伯特已經年紀老邁,並且正專注於邏 輯學,維格納主要是自己獨立進行研究。從1930年開始,維格納主要在美國普林斯頓大學 任教。他在1930年代的研究奠下了量子力學中對稱原理的基石。例如,他在1931年證明了 維格納定理(Wigner's theorem)。該定理說明每一個對稱變換都對應態空間中的一個幺正算子或反幺正算子。這是現代量子力學的基本定理。而本章提到的對粒子分類的方法, 稱為維格納分類法(Wigner's classification),便是由維格納於1939年發表的。維格納在 曼哈頓計劃中扮演着重要角色。 於1939年,維格納和另外兩位匈牙利物理學家建議愛因 斯坦去信美國總統羅斯福,信中表示了對德國核武發展的憂慮,並建議美國發展核武, 這促成了曼哈頓計劃。在曼哈頓計劃的進行中,維格納也是一核心人物。例如,世上第一 個核反應堆CP-1便是由他領導的團隊設計。1964年,基於維格納對於對稱原理的研究成 就,他獲頒諾貝爾物理學獎。維格納在老年時思想趨向哲學化。他在1960年發表的一篇文 章,名為《數學在自然科學中不合理的有效性》,是關於科學哲學的一篇經典文章。維 格納於1995年因肺炎離世,享年92歲。

尤金·維格納 (圖片來源:Wikimedia Commons)
註解:
1)代數結構指二元運算結構。也就是說,給定元素a和b,我們可定義它們的運算結果 a○b。最簡單的例子是實數的加法和乘法,其對應的運算○為+和×。另一例子是矩陣的 加法和乘法。文中提及的是一種很一般的抽象代數結構,稱為羣。
2)拓撲結構指個體在連續變化下的特征。例如,一個球體在連續變形下不能變成一個甜甜圈,所以球體和甜甜圈具有不同的拓撲結構。而由於甜甜圈可在連績變形下變成咖啡杯,甜甜圈和咖啡杯具有相同的拓撲結構。文中提及的是一般抽象空間,如一個羣的拓撲結構。
3) 羣的一個子集如果也是一個羣,那麼我們稱該子集為子羣(subgroup)。
4) 在第一章中,我們用粒子的角度來描述量子埸。例如,我們用光子的多粒子波函數來描述電磁埸。我們也可以用場的角度來描述電磁埸。也就是說,電磁場是位置的函數。而基於量子力學的隨機性,這函數並不確定,遵從一機率分佈。
延伸閱讀: