
巨觀與微觀之間非平衡的多尺度模型 Print Friendly and PDF
- Physics Today 專文
- 撰文者:林祉均譯
- 發文日期:2020-05-20
- 點閱次數:2806
人造材料經常展現出新穎有趣的非平衡性質:有些材料十分柔軟卻堅韌,有些能將廢熱轉化為電能,有些表現出奇特的流體行為。我們熟悉的虎克彈簧定律,以及描述流體的納維爾-斯托克斯方程式(Navier-Stokes equations),只對一般的傳統材料適用。如果要完整描述這些新穎材料的性質,則必須同時在巨觀和微觀的尺度上建立動力學模型。以下的討論盡可能使用最少的數學,希望說明這個新興的領域歡迎物理、數學、材料科學與工程各領域人才的加入。
首先是複雜流體,他們的違反直覺的行為會讓你大吃一驚。將旋轉的圓棒插入高分子溶液中,液體非但不會像水一樣出現凹陷下去的漩渦,反而還會沿著圓棒攀爬而上,稱為懷森堡效應(Weissenberg effect)。相同驚奇地,將一點黏稠的高分子溶液拉出容器外,會將容器內剩餘的溶液一同吸出,彷彿一條隱形的虹吸管。( 影片展示請見參考文獻1)
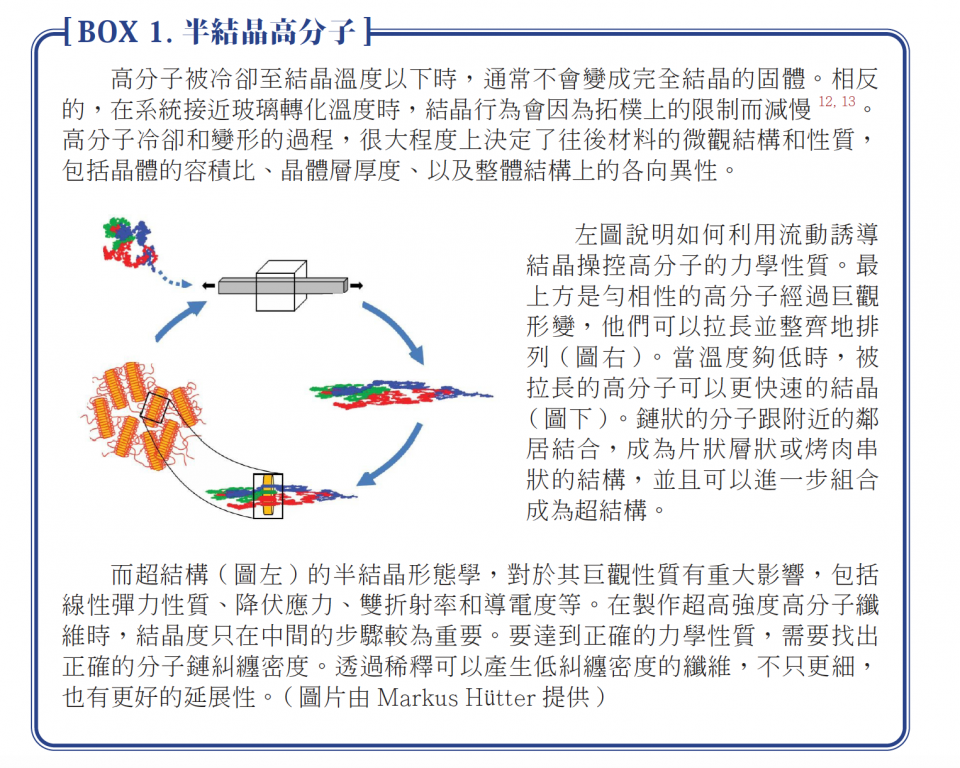
如果在材料變形後快速冷卻定形,它就會一直保持那樣。除非被加熱到玻璃轉化溫度以上,它才會恢復原本的形態。只要對固態高分子進行塑性變形,其中的鏈狀結構便會呈現一致的排列方向,形成非常強韌的材料。這類的纖維可以用於防切割手套, 或是航海用的輕量繩索。關於更多描述半結晶高分子材料,請參見BOX 1.。
另外,親水性的高分子能夠在水中交織成網絡,形成彈力十足的水凝膠。雖然雙網絡水凝膠主要是由水組成,卻能承受超過幾千萬帕斯卡的壓力。實驗證據顯示,水凝膠可以透過破壞其中一個網絡的共價鍵來分散能量,同時藉由僅剩的網絡來維持結構。
複雜行為的簡單描述
對於流體和固體的巨觀行為,連續介質力學的表述提供了一個很好的基礎。考慮連續介面的動量守恆,可以得到下面的運動方程式,稱為柯西動量方程式2:
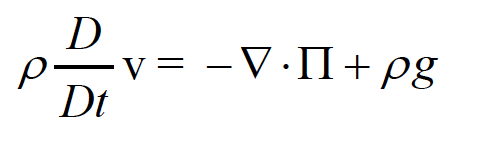
左側是質量密度ρ,以及巨觀流速v 對時間的微分,也就是加速度;右側描述的是連續介面上某一點的受力,包括應力張量Π 的散度,以及遍體力向量g。簡單來說其實就是F=ma。
此外還要加上一個假設:應力張量由兩個部分組成,包括來自各個方向的熱力學應力,還有一項正比於瞬時速度梯度的貢獻。這樣就得到了鼎鼎大名的納維爾-斯托克斯方程式(Navier-Stockes equation)。這項假設表示分子尺度的形變恢復的很快,以致於材料在微觀上可以被視為一直處於局域性平衡3。這個方程式能夠確保熵的變化量大於零,在直覺上很合理。像是水這樣的一般流體,個別分子很快能從形變中恢復,時間尺度比起整體應變率小許多,因此納維爾-斯托克斯方程式的描述非常準確。
不過像是高分子、蛋白質、膠體、液晶、乳狀液這類的材料,組成的分子單元較為龐大。這時候微觀的鬆弛速率和巨觀的應變率可能就會處在相同的時間尺度上,造成局域性平衡的假設不再成立。( 參見Byron Bird and Charles Curtiss, Physics Today, January 1984, page 36.)。研究人員早期就體認到納維爾-斯托克斯方程式在這方面的不足,並尋求相應的解方,因此開創了流變學這門學問。儘管柯西方程式(Cauchy's equation) 適用非常廣泛,但其中的應力張量Π 是個未知的變數,可能無法像一般流體那樣,被簡化成一項應力加上正比於速度梯度的項。複雜流體的模型需要建立在流體速度場之上,並另外考慮微觀分子的鬆弛時間,為原本單純的黏滯性描述加上彈力效應的影響。
如同流體力學,固體力學從線性動量守恆開始著手。不過最後的方程式通常是以拉格朗日變形場(Lagrangian deformation field)χ 來表示,相對於速度場來說是個更合理的選擇。在描述固體行為時,首先要做的簡化假設是應力張量和瞬時應變成正比,而瞬時應變又與χ 對空間的微分有關。可以預見的是,這樣的假設為我們的描述加上許多限制,對於複雜材料而言顯得不太合適。在複雜材料中,應力和應變之間可能有非線性關係,即便在形變量不大時亦然。如果你有試過把壞掉的衣架折回來,就知道有些固體形變無法回復。然而線性的彈力系統不會產生任何熵,因此應該要是可逆的才對。所以說,一個對複雜固體更精準的描述應該要能夠包含鬆弛效應。
綜合以上,我們看到流體的簡化圖像中只有耗散卻沒有彈性,微觀分子的鬆弛時間趨近於零;而固體卻只有彈性而沒有耗散,表示根本沒有鬆弛可言。顯然的,這兩種描述都需要進一步的拓展與補強,才能捕捉真實材料需要鬆弛時間的特性。
微結構要描述複雜固體與流體的行為,首先需要建立微結構的概念。描述這種結構的變數具有中等空間尺度 ( 可能是多個原子的大小和顯著的鬆弛時間,同時也跟原子尺度的動力學有直接連結。這樣一來,我們所需的變數就少了需多,至少比系統中的原子數少好幾個數量級。不過它們應該還是要稱職地描述系統中發生的物理現象,那麼這之間消失的自由度去了哪裡?我們通常把它們當作接近平衡狀態,也就是為那些鬆弛時間較長, 值得我們關心的自由度提供一個熱庫。
這些微結構變數是如何隨著方程式演化呢?利用實驗數據和分子模擬,我們可以發展出一個大致的物理圖像,這種方法稱為粗粒化建模。於是我們便想要問這三個問題:
什麼才是好用的微結構變數?
它們的演化遵循什麼方程式?
微結構變數和巨觀物理量 ( 例如應力)的關聯為何?
要回答這些問題需要洞察力、物理直覺、與創造力。系統性的解法通常不存在,但不論討論對象是流體還是固體,引入微結構的目標都是一樣的:準確的描述系統的鬆弛過程,而不再把它當作一瞬間發生。文中附上的三個說明框1,2,3,便是舉例微結構在連續介質問題中扮演的不同角色。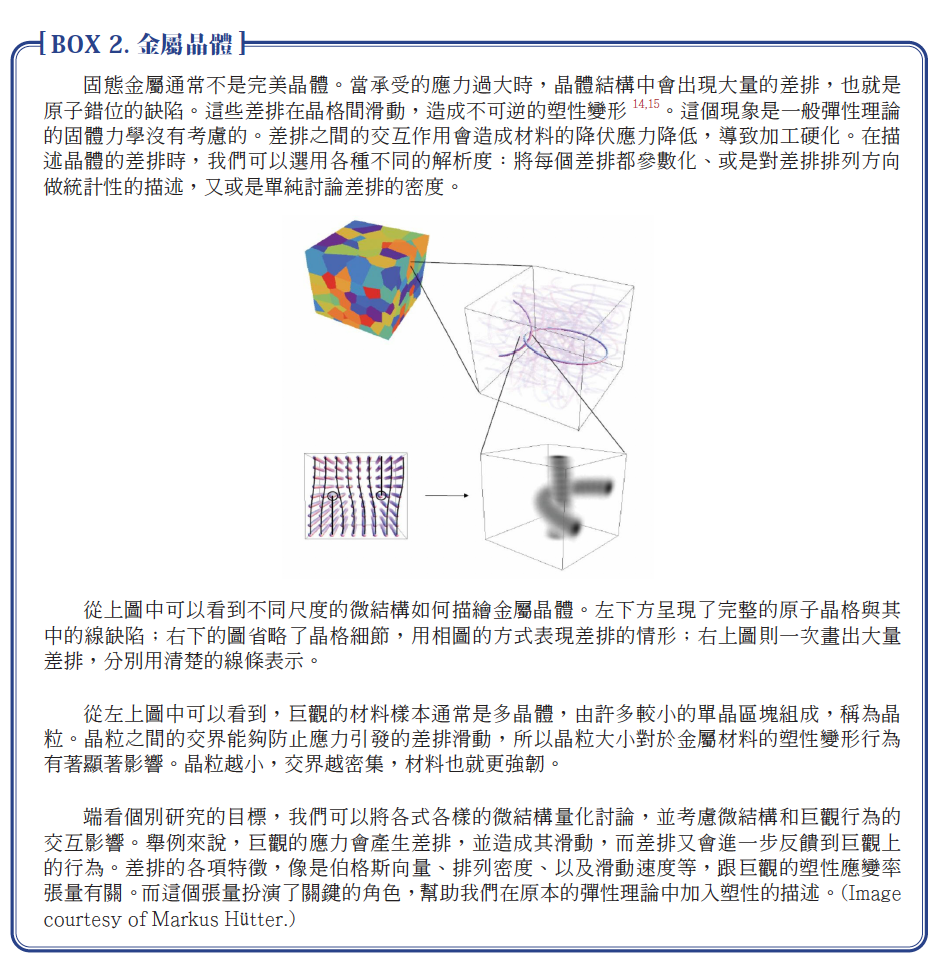

在複雜材料中找到一組可靠的變數至關重要。這些變數必須適當地包含微結構中的細節,只能捨棄不必要的部分。如此才能確保這些變數忠實地還原正確的物理圖像, 準確地描述各種觀察到的現象。舉例來說,一組微結構變數可能足以描述材料的機械性質、介電質行為、雙折射率,還能直接透過散射實驗得到材料結構。然而,我們應該只保留感興趣的物理性質,因為過度詳細的模型含有太多可調整參數,很可能變得過於累贅。
若巨觀與微觀之間的空間尺度差異過大,變數的選擇也要做出相對應的調整。一般來說,空間尺度和時間尺度上的落差往往伴隨而來,因此我們時常有機會可以利用漲落耗散定理來處理相關問題5。
在沒有前例可循的情況下,如何正確的選擇變數往往須要仰賴物理直覺。在粗粒化的過程中,如果我們想要得到新的物理,而不只是看到演算法跑出的結果,那麼憑感覺設變數可能是必要的一步。
在動力模型中引入微結構變數應該要能夠簡化模型,而不是使其更加複雜。微結構變數能夠將觀察結果用符合物理直覺的圖像來表達,同時連結看似毫不相關的不同面向。舉例來說,違反常理的懷森堡效應和隱形虹吸管,便可以透過高分子鏈糾纏的觀念來幫助闡明。
熱力學,加點摩擦力
多尺度動態系統的非平衡態熱力學建模,需要使用到統計力學推導出的熱動力位能( 像是亥姆霍茲自由能)。這種位能不只能決定靜止的物理量,也為微結構變數提供了鬆弛和流動的動態驅動力。同樣的,統計力學不只適用於體積這類的巨觀變量,也可以用於非平衡態的微結構變數。這個方法首先於1934 年由Werner Kuhn 用來描述高分子行為6。不過在微觀和巨觀的描述上,熵的值並不一樣,所以確保自由能在不同尺度下維持一致是很重要的。換句話說,將粗粒化過程分為兩個階段( 微觀原子尺度到介觀尺度,再到巨觀世界) 所得到的自由能,應該要跟直接一步連結微觀與巨觀的粗粒化過程相同。
熱動力位能也幫助我們透過最少的現象學,就能揭開應力張量Π 的神秘面紗。熱力學條件看似是嚴苛的限制,但卻是我們探索路程上的一大助力。只有遵從這些限制的微變數模型,才能確保自己免於觸犯戒律,像是憑空創造能量或是減少宇宙中的熵4。
一旦選好了微結構變數,就會需要相對應的演化方程式。當然,這些方程式必須遵守基本的物理法則,例如熱力學第一和第二定律,以及漲落耗散定理(fluctuation-dissipation theorem)。除此之外,方程式中的某些參數值( 像是摩擦力係數),可能得透過分子動力學模擬或其他更細部的物理描述來獲得。在實務上,這代表系統的動力學或許需要三個不同層次來描述:原子尺度、微結構、以及連續介質。在我們確定各種參數的值後,原子尺度的動力學模擬便可以先放到一旁。此時我們的模型便剩下兩組變數:微觀和巨觀。或者更精確地來說,應該是介觀和巨觀。在進行模擬時,這兩個不同世界必須持續地進行對話。
不是獨白,而是雙向對話
多尺度模型將巨觀的動力學圖像和介觀結構的動態演化連結在一起。一般在流體和固體力學中使用的方程式掌管巨觀物理量的時間演化,而藉由引入微結構,我們能獲得更精細的描述。巨觀與微觀之間的關係不只緊密,而且是雙向的:巨觀的形變造成微結構扭曲,而後者反過來給巨觀結構帶來非平衡態時的應力。因此,應力張量並不能直接用巨觀的速度或位移梯度來表示,而是需要考慮介觀結構的狀態。這種情況並不少見, 而雙向溝通的建立往往需要仰賴非平衡態熱力學,藉以確保模型和基本物理定律是相容的4。
儘管熱動力位能的空間導數是系統演化的主要動力,但還要加上摩擦力傳輸係數才能完整描述鬆弛現象。摩擦力會隨著描述的粗粒化程度逐漸增加,就像熵一樣。而這個概念也就是著名的漲落耗散定理。簡單來說,某個尺度上的速度或力量漲落,可以連結到更大尺度上的摩擦力耗散。這個定理原先是從無摩擦力的命定性系統推導出,用來為粗粒化動力學添加適當的限制。
一個好的模型應該是個定義良好的數學物件,而不只是電腦中的演算法。而數學物件應該要能嚴格遵守熱力學規範。如果一個模型存在漸近解,那我們也可以拿他來測試演算法是否會在相同條件下收斂。在我們( 原作者) 自己的研究中,我們用環- 鎖鏈模型的數學形式推導出圖像處理演算法。同時利用平行演算法,讓平價顯示卡跑模擬的速度比一般處理器快上兩個數量級,而且給出同樣的結果。要是沒有一個定義良好的數學物件,這種程度的速度提升是不可能辦到的。
在建模時採用非平衡態熱力學,能夠確保模型滿足各種限制條件,包括熱力學第一和第二定律。而數值演算的結果也必須收斂到一個熱力學上合理的結果。更進一步來說,熱力學能限制離散的動態演化,讓演算法的數值模擬更加穩定7。
跟著微結構一起流動
多尺度分析最典型的例子,就是高分子系統。其中最簡單,鬆弛時間最長的微結構變數就是構形張量:
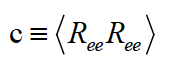
Ree 是高分子端點間向量,放在<⋅⋅⋅> 中取系綜平均。高分子鏈在流場中被拉伸時, 造成熵值下降。不過這時候系統的能量並沒有顯著的改變,因此高分子會受到熱力學驅使,強烈地想要縮回原本各向同性的較短構形。這個收縮過程自然導致了正向應力和剪應力,兩者都經常在高分子系統中出現。例如文章開頭提到的懷森堡效應,就是因為具有方向性的正向應力,稱為環應力。這股應力順著彎曲的流線方向提供張力,將高分子流體向內擠壓,因此沿著旋轉的圓柱攀爬而上。
此外,像是原子模擬的數值結果,或是真實物理系統的散射性質,都可以放入構形張量。因此它是個有力的工具,能夠輕易地把簡易的分子圖像和巨觀現象連結起來。
不過情況並不總是那麼順利。濃縮高分子中,分子鏈的不可交叉性會導致糾纏出現8。
糾纏之間的距離界於高分子的持久長度和平均高分子膠聯大小,並且與分子重量無關。Masao Doi 和Sam Edwards 在1970 年代發表了數篇文章,當中提出了一個構想: 在高分子的特定區段內圈出一個管狀區域,並利用管子方向的機率分布來描述高分子的微結構。只需要這種程度的描述,再加上一點各向異性的動力學,這個管子模型就能準確地符合非線性應變流實驗中應力鬆弛的情形。( 關於高分子糾纏的訊息,可以參見由Tom McLeish 撰寫的文章, Physics Today, August 2008, page 40)
不過Doi 和Edwards 提出的單一區段理論無法提供量化的預測,也不能描述其他細部現象。其他更詳細的模型因而爭相角逐發展,其中我們在BOX 3. 中討論到的環- 鎖鏈模型9 成功地描述熔融態高分子的糾纏行為。其中的微結構變數包含糾纏數量的漲落,糾纏間隔,以及糾纏之間的單體密度,而這些參數都可以用電腦模擬找出。由於環- 鎖鏈模型帶有較精細的描述,這樣的模型(BOX 3.) 可以擷取到高分子融化時更廣泛的現象。
現在鬆弛還太早
多尺度模型的領域中,還有許多新的機會等待我們探索。舉例來說,差排引起的塑性性質可能在時間尺度上沒有明顯的大小分別10,這代表著漲落耗散定理可能不再被遵守。這類時間尺度大小的問題有待更深入的研究。
材料的脆性破裂,也是由巨觀與微觀之間的對話所掌控,因此讓它成為多尺度建模的良好人選。不過它和上述的許多例子有些不同。上面提到的各種微結構廣泛存在於連續介質中各處,因此特定效應可以相互抵銷。不過在破裂的情形中,彈性的連續介質中突然出現一個裂縫尖端。這個尖端周遭的應力場影響範圍較大,而且持續驅使破裂過程繼續進行,然而裂縫尖端本身卻是微觀尺度。因此遠離尖端的區域適用連續介質力學, 在尖端附近則需要使用原子動力學,或甚至是量子力學。銜接這兩個差異甚大的區域, 需要複雜而巧妙的手法。多尺度模型可以整合不同時間與空間尺度上的差異,因此或許能為脆性破裂提供一個更細緻的進階模型。
雖然這篇文章著重在材料面對形變時的反應,不過在溫度梯度或電磁場等其他刺激下,同樣的議題又會再度浮現。這時候,多尺度動力學模型的細節,例如變數的選擇和建模方式,便取決於研究針對的是何種環境刺激或物理現象。不過整體而言,這裡討論到的各種基本概念依然適用。另外,多成分材料和粗粒化的主動物質( 例如凝膠中的分子馬達或是群游的雙性(Janus) 顆粒) 所面臨的問題,或許也能從多尺度模型中受益。
微結構變數不該僅僅被視為數學上必要的簡化。成功的粗粒化能帶來深刻的物理意涵,不只解釋了現象,也幫助科學家獲得分子工程所需的直覺。在粗粒化描述的協助之下,原子模擬才能發揮最高的效用,並汲取有用的資訊。即便粗粒化並不成功,也還是帶來了新的資訊,代表為其所使用的假設有所缺漏。一個粗粒化模型如果省略了某些關鍵的物理成分,造成不符合實驗結果,這樣的結果本身便提供重要訊息。所以別為了粗粒化道歉,相反的,你其實沒有理由不去做11。
不論在基礎概念還是實際應用的層面上,高分子纏結的研究仍存在許多懸而未解的難題。需要深刻的物理思維和創見,才能為這些難題找到合適的解方。也就是說,儘管機器學習的快速發展帶來出色的成果,但恐怕沒辦法為這些問題找到正確的模型。這些領域需要的是更多物理腦袋的投入。
在發展多尺度模型可靠演算法上有很多進步,但是每一個新的模型都帶來前所未見的計算挑戰。這方面就需要基礎和應用數學家的貢獻。從純數學的角度來看,多尺度模型所使用的數學工具便已十分有趣。不僅如此,他們也在工程領域有很大的潛力,可以幫助我們設計出需要的非平衡特殊性質的高分子。
感謝與以下人員的啟發性討論 Marc Geers, Varvara Kouznetsova, and Theo Tervoort. JaySchieber 感謝 David Venerus 對於本文的重要回饋.
Physics Today 73, 3, 36 (2020); https://doi.org/10.1063/PT.3.4430
本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於Physics Today, January 2020 雜誌內(Physics Today 73, 3, 36 (2020) https://physicstoday.scitation. org/doi/10.1063/PT.3.4430;原文作者:Jay Schieber、Markus Hütter。中文編譯:林祉均,國立清華大學物理系 學生。
Physics Bimonthly (The Physics Society of Taiwan) appreciates that Physics Today (American Institute of Physics) authorizes Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by on Physics Today 73, 3, 36 (2020) https://physicstoday.scitation.org/ doi/10.1063/PT.3.4430 The article in Mandarin is translated and edited by J. R. Lin , working on Department of Physics, National Tsing Hua University.
原文作者
Jay Schieber,伊利諾理工學院( 芝加哥)(Illinois Institute of Technology in Chicago), 物理學、化學工程、應用數學教授, 任職於凝態軟物質分子研究中心。
Markus Hütter, 荷蘭埃因霍溫理工大學 (Eindhoven University of Technology in the Netherlands),高分子多尺度分析副教授,任職於機械工程系高分子科技組。
譯者
林祉均
國立清華大學物理系
首先是複雜流體,他們的違反直覺的行為會讓你大吃一驚。將旋轉的圓棒插入高分子溶液中,液體非但不會像水一樣出現凹陷下去的漩渦,反而還會沿著圓棒攀爬而上,稱為懷森堡效應(Weissenberg effect)。相同驚奇地,將一點黏稠的高分子溶液拉出容器外,會將容器內剩餘的溶液一同吸出,彷彿一條隱形的虹吸管。( 影片展示請見參考文獻1)

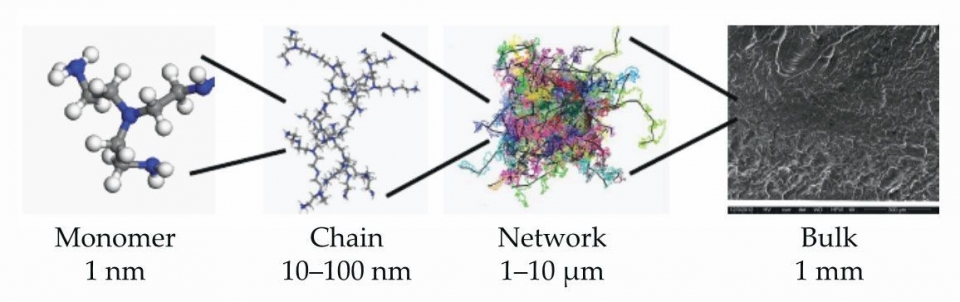
圖一;在不同尺度上,高分子材料呈現不同的結構。當材料遭到彎曲變形,單一分子只需幾皮秒就能恢復原樣,整個塊材卻需要數小時或甚至好幾年。多尺度材料的模型必須要能夠描繪不同空間和時間尺度上的結構動力學。(Adapted from Y. Li et al., Polymers 5, 751, 2013, doi:10 .3390/polym5020751.)
固態材料的奇特性質也不遑多讓。在冷卻接近玻璃轉化溫度時,高分子表現得很像是固體,不過還未完全結晶。此時系統動態變得十分緩慢,因此高分子材料很少能在冷卻過程中達到熱平衡。而且在實務上,高分子並沒有均勻到可以形成完美的晶體。因此完整結晶的高分子固體是很少見的。如果在材料變形後快速冷卻定形,它就會一直保持那樣。除非被加熱到玻璃轉化溫度以上,它才會恢復原本的形態。只要對固態高分子進行塑性變形,其中的鏈狀結構便會呈現一致的排列方向,形成非常強韌的材料。這類的纖維可以用於防切割手套, 或是航海用的輕量繩索。關於更多描述半結晶高分子材料,請參見BOX 1.。

另外,親水性的高分子能夠在水中交織成網絡,形成彈力十足的水凝膠。雖然雙網絡水凝膠主要是由水組成,卻能承受超過幾千萬帕斯卡的壓力。實驗證據顯示,水凝膠可以透過破壞其中一個網絡的共價鍵來分散能量,同時藉由僅剩的網絡來維持結構。
複雜行為的簡單描述
對於流體和固體的巨觀行為,連續介質力學的表述提供了一個很好的基礎。考慮連續介面的動量守恆,可以得到下面的運動方程式,稱為柯西動量方程式2:
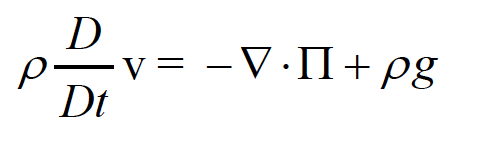
左側是質量密度ρ,以及巨觀流速v 對時間的微分,也就是加速度;右側描述的是連續介面上某一點的受力,包括應力張量Π 的散度,以及遍體力向量g。簡單來說其實就是F=ma。
此外還要加上一個假設:應力張量由兩個部分組成,包括來自各個方向的熱力學應力,還有一項正比於瞬時速度梯度的貢獻。這樣就得到了鼎鼎大名的納維爾-斯托克斯方程式(Navier-Stockes equation)。這項假設表示分子尺度的形變恢復的很快,以致於材料在微觀上可以被視為一直處於局域性平衡3。這個方程式能夠確保熵的變化量大於零,在直覺上很合理。像是水這樣的一般流體,個別分子很快能從形變中恢復,時間尺度比起整體應變率小許多,因此納維爾-斯托克斯方程式的描述非常準確。
不過像是高分子、蛋白質、膠體、液晶、乳狀液這類的材料,組成的分子單元較為龐大。這時候微觀的鬆弛速率和巨觀的應變率可能就會處在相同的時間尺度上,造成局域性平衡的假設不再成立。( 參見Byron Bird and Charles Curtiss, Physics Today, January 1984, page 36.)。研究人員早期就體認到納維爾-斯托克斯方程式在這方面的不足,並尋求相應的解方,因此開創了流變學這門學問。儘管柯西方程式(Cauchy's equation) 適用非常廣泛,但其中的應力張量Π 是個未知的變數,可能無法像一般流體那樣,被簡化成一項應力加上正比於速度梯度的項。複雜流體的模型需要建立在流體速度場之上,並另外考慮微觀分子的鬆弛時間,為原本單純的黏滯性描述加上彈力效應的影響。
如同流體力學,固體力學從線性動量守恆開始著手。不過最後的方程式通常是以拉格朗日變形場(Lagrangian deformation field)χ 來表示,相對於速度場來說是個更合理的選擇。在描述固體行為時,首先要做的簡化假設是應力張量和瞬時應變成正比,而瞬時應變又與χ 對空間的微分有關。可以預見的是,這樣的假設為我們的描述加上許多限制,對於複雜材料而言顯得不太合適。在複雜材料中,應力和應變之間可能有非線性關係,即便在形變量不大時亦然。如果你有試過把壞掉的衣架折回來,就知道有些固體形變無法回復。然而線性的彈力系統不會產生任何熵,因此應該要是可逆的才對。所以說,一個對複雜固體更精準的描述應該要能夠包含鬆弛效應。
綜合以上,我們看到流體的簡化圖像中只有耗散卻沒有彈性,微觀分子的鬆弛時間趨近於零;而固體卻只有彈性而沒有耗散,表示根本沒有鬆弛可言。顯然的,這兩種描述都需要進一步的拓展與補強,才能捕捉真實材料需要鬆弛時間的特性。
微結構要描述複雜固體與流體的行為,首先需要建立微結構的概念。描述這種結構的變數具有中等空間尺度 ( 可能是多個原子的大小和顯著的鬆弛時間,同時也跟原子尺度的動力學有直接連結。這樣一來,我們所需的變數就少了需多,至少比系統中的原子數少好幾個數量級。不過它們應該還是要稱職地描述系統中發生的物理現象,那麼這之間消失的自由度去了哪裡?我們通常把它們當作接近平衡狀態,也就是為那些鬆弛時間較長, 值得我們關心的自由度提供一個熱庫。
這些微結構變數是如何隨著方程式演化呢?利用實驗數據和分子模擬,我們可以發展出一個大致的物理圖像,這種方法稱為粗粒化建模。於是我們便想要問這三個問題:
什麼才是好用的微結構變數?
它們的演化遵循什麼方程式?
微結構變數和巨觀物理量 ( 例如應力)的關聯為何?
要回答這些問題需要洞察力、物理直覺、與創造力。系統性的解法通常不存在,但不論討論對象是流體還是固體,引入微結構的目標都是一樣的:準確的描述系統的鬆弛過程,而不再把它當作一瞬間發生。文中附上的三個說明框1,2,3,便是舉例微結構在連續介質問題中扮演的不同角色。


在複雜材料中找到一組可靠的變數至關重要。這些變數必須適當地包含微結構中的細節,只能捨棄不必要的部分。如此才能確保這些變數忠實地還原正確的物理圖像, 準確地描述各種觀察到的現象。舉例來說,一組微結構變數可能足以描述材料的機械性質、介電質行為、雙折射率,還能直接透過散射實驗得到材料結構。然而,我們應該只保留感興趣的物理性質,因為過度詳細的模型含有太多可調整參數,很可能變得過於累贅。
若巨觀與微觀之間的空間尺度差異過大,變數的選擇也要做出相對應的調整。一般來說,空間尺度和時間尺度上的落差往往伴隨而來,因此我們時常有機會可以利用漲落耗散定理來處理相關問題5。
在沒有前例可循的情況下,如何正確的選擇變數往往須要仰賴物理直覺。在粗粒化的過程中,如果我們想要得到新的物理,而不只是看到演算法跑出的結果,那麼憑感覺設變數可能是必要的一步。
在動力模型中引入微結構變數應該要能夠簡化模型,而不是使其更加複雜。微結構變數能夠將觀察結果用符合物理直覺的圖像來表達,同時連結看似毫不相關的不同面向。舉例來說,違反常理的懷森堡效應和隱形虹吸管,便可以透過高分子鏈糾纏的觀念來幫助闡明。
熱力學,加點摩擦力
多尺度動態系統的非平衡態熱力學建模,需要使用到統計力學推導出的熱動力位能( 像是亥姆霍茲自由能)。這種位能不只能決定靜止的物理量,也為微結構變數提供了鬆弛和流動的動態驅動力。同樣的,統計力學不只適用於體積這類的巨觀變量,也可以用於非平衡態的微結構變數。這個方法首先於1934 年由Werner Kuhn 用來描述高分子行為6。不過在微觀和巨觀的描述上,熵的值並不一樣,所以確保自由能在不同尺度下維持一致是很重要的。換句話說,將粗粒化過程分為兩個階段( 微觀原子尺度到介觀尺度,再到巨觀世界) 所得到的自由能,應該要跟直接一步連結微觀與巨觀的粗粒化過程相同。
熱動力位能也幫助我們透過最少的現象學,就能揭開應力張量Π 的神秘面紗。熱力學條件看似是嚴苛的限制,但卻是我們探索路程上的一大助力。只有遵從這些限制的微變數模型,才能確保自己免於觸犯戒律,像是憑空創造能量或是減少宇宙中的熵4。
一旦選好了微結構變數,就會需要相對應的演化方程式。當然,這些方程式必須遵守基本的物理法則,例如熱力學第一和第二定律,以及漲落耗散定理(fluctuation-dissipation theorem)。除此之外,方程式中的某些參數值( 像是摩擦力係數),可能得透過分子動力學模擬或其他更細部的物理描述來獲得。在實務上,這代表系統的動力學或許需要三個不同層次來描述:原子尺度、微結構、以及連續介質。在我們確定各種參數的值後,原子尺度的動力學模擬便可以先放到一旁。此時我們的模型便剩下兩組變數:微觀和巨觀。或者更精確地來說,應該是介觀和巨觀。在進行模擬時,這兩個不同世界必須持續地進行對話。
不是獨白,而是雙向對話
多尺度模型將巨觀的動力學圖像和介觀結構的動態演化連結在一起。一般在流體和固體力學中使用的方程式掌管巨觀物理量的時間演化,而藉由引入微結構,我們能獲得更精細的描述。巨觀與微觀之間的關係不只緊密,而且是雙向的:巨觀的形變造成微結構扭曲,而後者反過來給巨觀結構帶來非平衡態時的應力。因此,應力張量並不能直接用巨觀的速度或位移梯度來表示,而是需要考慮介觀結構的狀態。這種情況並不少見, 而雙向溝通的建立往往需要仰賴非平衡態熱力學,藉以確保模型和基本物理定律是相容的4。
儘管熱動力位能的空間導數是系統演化的主要動力,但還要加上摩擦力傳輸係數才能完整描述鬆弛現象。摩擦力會隨著描述的粗粒化程度逐漸增加,就像熵一樣。而這個概念也就是著名的漲落耗散定理。簡單來說,某個尺度上的速度或力量漲落,可以連結到更大尺度上的摩擦力耗散。這個定理原先是從無摩擦力的命定性系統推導出,用來為粗粒化動力學添加適當的限制。
一個好的模型應該是個定義良好的數學物件,而不只是電腦中的演算法。而數學物件應該要能嚴格遵守熱力學規範。如果一個模型存在漸近解,那我們也可以拿他來測試演算法是否會在相同條件下收斂。在我們( 原作者) 自己的研究中,我們用環- 鎖鏈模型的數學形式推導出圖像處理演算法。同時利用平行演算法,讓平價顯示卡跑模擬的速度比一般處理器快上兩個數量級,而且給出同樣的結果。要是沒有一個定義良好的數學物件,這種程度的速度提升是不可能辦到的。
在建模時採用非平衡態熱力學,能夠確保模型滿足各種限制條件,包括熱力學第一和第二定律。而數值演算的結果也必須收斂到一個熱力學上合理的結果。更進一步來說,熱力學能限制離散的動態演化,讓演算法的數值模擬更加穩定7。
跟著微結構一起流動
多尺度分析最典型的例子,就是高分子系統。其中最簡單,鬆弛時間最長的微結構變數就是構形張量:
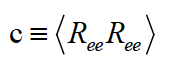
Ree 是高分子端點間向量,放在<⋅⋅⋅> 中取系綜平均。高分子鏈在流場中被拉伸時, 造成熵值下降。不過這時候系統的能量並沒有顯著的改變,因此高分子會受到熱力學驅使,強烈地想要縮回原本各向同性的較短構形。這個收縮過程自然導致了正向應力和剪應力,兩者都經常在高分子系統中出現。例如文章開頭提到的懷森堡效應,就是因為具有方向性的正向應力,稱為環應力。這股應力順著彎曲的流線方向提供張力,將高分子流體向內擠壓,因此沿著旋轉的圓柱攀爬而上。
此外,像是原子模擬的數值結果,或是真實物理系統的散射性質,都可以放入構形張量。因此它是個有力的工具,能夠輕易地把簡易的分子圖像和巨觀現象連結起來。
不過情況並不總是那麼順利。濃縮高分子中,分子鏈的不可交叉性會導致糾纏出現8。
糾纏之間的距離界於高分子的持久長度和平均高分子膠聯大小,並且與分子重量無關。Masao Doi 和Sam Edwards 在1970 年代發表了數篇文章,當中提出了一個構想: 在高分子的特定區段內圈出一個管狀區域,並利用管子方向的機率分布來描述高分子的微結構。只需要這種程度的描述,再加上一點各向異性的動力學,這個管子模型就能準確地符合非線性應變流實驗中應力鬆弛的情形。( 關於高分子糾纏的訊息,可以參見由Tom McLeish 撰寫的文章, Physics Today, August 2008, page 40)
不過Doi 和Edwards 提出的單一區段理論無法提供量化的預測,也不能描述其他細部現象。其他更詳細的模型因而爭相角逐發展,其中我們在BOX 3. 中討論到的環- 鎖鏈模型9 成功地描述熔融態高分子的糾纏行為。其中的微結構變數包含糾纏數量的漲落,糾纏間隔,以及糾纏之間的單體密度,而這些參數都可以用電腦模擬找出。由於環- 鎖鏈模型帶有較精細的描述,這樣的模型(BOX 3.) 可以擷取到高分子融化時更廣泛的現象。
現在鬆弛還太早
多尺度模型的領域中,還有許多新的機會等待我們探索。舉例來說,差排引起的塑性性質可能在時間尺度上沒有明顯的大小分別10,這代表著漲落耗散定理可能不再被遵守。這類時間尺度大小的問題有待更深入的研究。
材料的脆性破裂,也是由巨觀與微觀之間的對話所掌控,因此讓它成為多尺度建模的良好人選。不過它和上述的許多例子有些不同。上面提到的各種微結構廣泛存在於連續介質中各處,因此特定效應可以相互抵銷。不過在破裂的情形中,彈性的連續介質中突然出現一個裂縫尖端。這個尖端周遭的應力場影響範圍較大,而且持續驅使破裂過程繼續進行,然而裂縫尖端本身卻是微觀尺度。因此遠離尖端的區域適用連續介質力學, 在尖端附近則需要使用原子動力學,或甚至是量子力學。銜接這兩個差異甚大的區域, 需要複雜而巧妙的手法。多尺度模型可以整合不同時間與空間尺度上的差異,因此或許能為脆性破裂提供一個更細緻的進階模型。
雖然這篇文章著重在材料面對形變時的反應,不過在溫度梯度或電磁場等其他刺激下,同樣的議題又會再度浮現。這時候,多尺度動力學模型的細節,例如變數的選擇和建模方式,便取決於研究針對的是何種環境刺激或物理現象。不過整體而言,這裡討論到的各種基本概念依然適用。另外,多成分材料和粗粒化的主動物質( 例如凝膠中的分子馬達或是群游的雙性(Janus) 顆粒) 所面臨的問題,或許也能從多尺度模型中受益。
微結構變數不該僅僅被視為數學上必要的簡化。成功的粗粒化能帶來深刻的物理意涵,不只解釋了現象,也幫助科學家獲得分子工程所需的直覺。在粗粒化描述的協助之下,原子模擬才能發揮最高的效用,並汲取有用的資訊。即便粗粒化並不成功,也還是帶來了新的資訊,代表為其所使用的假設有所缺漏。一個粗粒化模型如果省略了某些關鍵的物理成分,造成不符合實驗結果,這樣的結果本身便提供重要訊息。所以別為了粗粒化道歉,相反的,你其實沒有理由不去做11。
不論在基礎概念還是實際應用的層面上,高分子纏結的研究仍存在許多懸而未解的難題。需要深刻的物理思維和創見,才能為這些難題找到合適的解方。也就是說,儘管機器學習的快速發展帶來出色的成果,但恐怕沒辦法為這些問題找到正確的模型。這些領域需要的是更多物理腦袋的投入。
在發展多尺度模型可靠演算法上有很多進步,但是每一個新的模型都帶來前所未見的計算挑戰。這方面就需要基礎和應用數學家的貢獻。從純數學的角度來看,多尺度模型所使用的數學工具便已十分有趣。不僅如此,他們也在工程領域有很大的潛力,可以幫助我們設計出需要的非平衡特殊性質的高分子。
感謝與以下人員的啟發性討論 Marc Geers, Varvara Kouznetsova, and Theo Tervoort. JaySchieber 感謝 David Venerus 對於本文的重要回饋.
Physics Today 73, 3, 36 (2020); https://doi.org/10.1063/PT.3.4430
本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於Physics Today, January 2020 雜誌內(Physics Today 73, 3, 36 (2020) https://physicstoday.scitation. org/doi/10.1063/PT.3.4430;原文作者:Jay Schieber、Markus Hütter。中文編譯:林祉均,國立清華大學物理系 學生。
Physics Bimonthly (The Physics Society of Taiwan) appreciates that Physics Today (American Institute of Physics) authorizes Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by on Physics Today 73, 3, 36 (2020) https://physicstoday.scitation.org/ doi/10.1063/PT.3.4430 The article in Mandarin is translated and edited by J. R. Lin , working on Department of Physics, National Tsing Hua University.
原文作者
Jay Schieber,伊利諾理工學院( 芝加哥)(Illinois Institute of Technology in Chicago), 物理學、化學工程、應用數學教授, 任職於凝態軟物質分子研究中心。
Markus Hütter, 荷蘭埃因霍溫理工大學 (Eindhoven University of Technology in the Netherlands),高分子多尺度分析副教授,任職於機械工程系高分子科技組。
譯者
林祉均
國立清華大學物理系