我們與量子計算的距離

量子計算的研究已經開始逐漸成熟了，尤其拜最近量子位元 (quantum bit 或簡稱 qubit) 工程的進步所賜，一連串的物理實驗可以使用為數不多的量子位元就成功地展示其計算能力。但除了小型、實驗室規模、原則性 (proof of principle) 的元件之外有許多企業也開始想辦法將這種能力運用到可擴展 (scalable) 的量子計算系統上，希望能將上千萬個邏輯量子位元放入可商用的完整量子計算系統，藉由量子科技的能力解決傳統電腦無法應付的實際問題。

量子計算的研究在數學和物理的領域裡並非新鮮事，但主要都聚焦在量子位元和量子演算法 (quantum algorithm) 這兩個部份。量子位元的研究著重於實驗元件裡量子位元的製造、操作和效能評估，而迪文森佐準則 (DiVincenzo criteria) 列出了提供了要在真實物理系統裡做量子計算最基本要滿足的運作狀態₁同時也變成了研究的主流方向。至於量子演算法的研究則是著重在發展可以使用在理想量子位元上的演算法₂，不過最近也已經開始打造能夠用於真實量子位元的相關演算法₃。但整體來說，就像傳統電腦的組成不只有軟體和電晶體，單單只有量子演算法和量子位元也不可能構成真正的量子計算系統。

 

要如何打造一套量子計算系統可以自動地將輸入的量子演算法放到量子位元上運行？現在已經有研究人員開始在制定基本運作方法的架構層_4,5 (architectrual layer)，部分的運作方法可以在圖一裡找到，不過其餘完整操作方法和可複製量子計算系統的部分還沒有什麼具體的想法。

 

“  要建造真正可擴展量子電腦需要跨領域技術的人才，所以有心願意跨領域的人有福了，因為這類系統的設計師現在正遇到一些橫跨物理、工程和電腦架構領域的難題。”    
 

 

應用導向的設計

量子演算法到底是怎麼設計出來、又怎麼在真實量子位元上執行？首先要把演算法變成一連串的邏輯運算 (logical operation) 或稱量子閘 (gate，有時也稱量子邏輯閘) 組成的量子電路 (quantum circuit，請見註解一)。接下來設計師透過物理上的對稱性將電路簡化，使演算法可以在現今這種為數不多的真實量子位元系統上執行。不過目前量子演算法的最佳化還沒辦法完全靠電腦做，而其中最頭痛的步驟到目前都還是純手工處理。不過有了軟體的幫助，設計師就可以透過分析同調時間 (coherence time)、量子閘保真度 (gate fidelity) 和演算法的近似方法等變數如何影響結果的準確性來估算所需要的量子位元和量子閘的數量。但最佳化工具應該還是要設計成不需要人工就可以簡化演算法，例如這些工具應該要很快地生出各種不同但等價的么正轉換 (unitary transformation) 電路讓設計師從中選出最好的一個。

 

現在已經有一些程式設計環境已經可以讓編譯器執行一些演算法的初步優化且使這些演算法可以做資源分析 (resource analysis)、模擬或在特定類型的量子位元上執行。基本上編譯器做的事情就是把量子電路轉譯成稱為量子組合語言 (QASM，quantum assembly language) 的一系列量子邏輯指令 (logical quantum instruction)。量子電路在這種文字格式的程式語言下變成一系列的操作指令，而這些指令會根據演算法告訴各個量子位元當下該做什麼事。

 

 

從演算法設計師的角度來看，QASM 的程式碼已經可以在真實的量子位元系統上執行了。但不幸的是並非所有類型的量子位元系統都與 QSMA 定義的量子閘相容，畢竟量子位元的製造原料不只有一種，而這些材料會決定哪些量子閘是物理性質直接給定的。這樣子的量子閘被稱為天然閘 (native gate) ，因為這些會因量子位元系統不同而有所改變，所以這些 QASM 的邏輯操作必須先將量子閘轉換成天然閘的組合。即便如此，研究人員還是必須考量會影響系統設計和架構的因素，譬如演算法裡哪些量子邏輯操作是可以直接在量子位元上運作的。不能直接運作的要怎麼找到等價的量子閘或是一組量子閘替代？哪些量子閘可以平行運算？連續幾個量子閘的操作後保真度或誤差還在可以接受的範圍內？

 

當選擇了適當的邏輯操作和量子位元的種類後研究人員就可以將一系列的天然閘放到真實的系統上執行。雖然從設計演算法的角度來看，系統內任意兩個量子位元之間都應當可以執行雙量子位元量子閘 (two-qubit gate) 操作，不過在許多系統裡要做雙位元操作必須要兩個量子位元靠夠近才辦得到。所以演算法必須要投射 (mapping) 到量子位元網格 (qubit grid) 裡可以執行操作的量子位元上並在量子元件諸多的限制下決定最佳操作順序或平行運算。
 

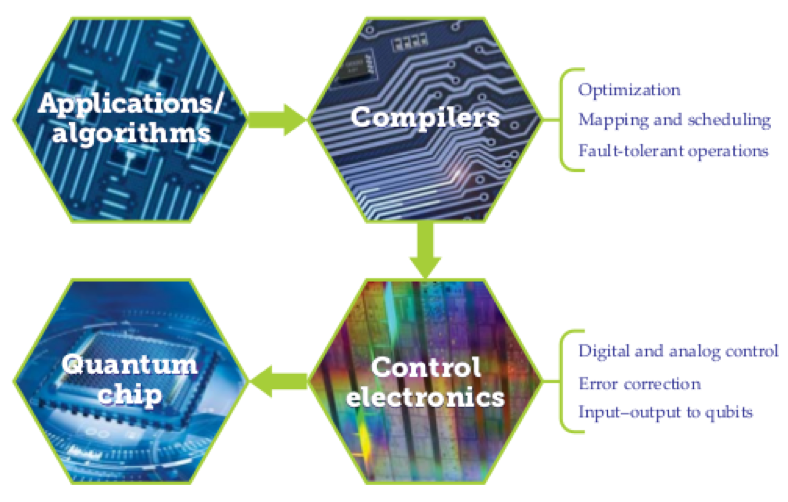
圖一、量子電腦的必要運作功能。應用導向的設計可以幫助決定如何製造在特定應用區加速演算的系統。(Applications/algorithms: Jay M. Gambetta, Jerry M. Chow, and Matthias Steffen, CC BY 4.0; compilers: iStock.com/Bet_Noire; control electronics: Steve Jurvetson, CC BY 2.0; quantum chip: Yurchanka Siarhei/shutterstock.com.)


 

 

演算法的操作要投射到量子位元上和做排程並不簡單，畢竟大多數量子位元裝置之間的連接非常受限，通常只有最靠近的兩個量子位元才有連結；因此要決定哪個量子位元可以拿來執行操作也必須考慮這一層關係。如果要操作較遠的量子位元就需要透過訊息穿梭 (shuttling) 或量子遙傳 (quantum teleportation)，但如此一來會大大地削弱跑演算法的可用量子資源₆。投射和安排通訊協定 (protocol) 更是個困難的挑戰，因為真實的量子位元算是出了名的脆弱且雜訊多，所以製作協定還必須要把這些缺陷列入考量。

 

確保量子電腦每次運算的初始狀態盡可能地一致對所有演算法執行也很重要，畢竟量子演算法必須要重複運算多次才能得到統計上有意義的結果。通常演算的執行過程要跑好幾千次，所以必須要又快又準確才能避免量子電路被多餘的誤差來源影響。

 

傳統計算需要做誤差校正才能確保運作的可靠性，量子計算當然也不例外；不過傳統的誤差校正協定 (error-correcting protocol) 沒辦法直接用在量子計算上，因為就像傳統電腦的位元，個別量子位元所攜帶的資訊也會被環境雜訊破壞，不過會干擾量子計算的誤差來源比傳統的還要多、影響也更大。量子誤差校正方法裡包含了在多個量子位元之間編入一個邏輯量子位元態 (logical qubit state) 且用測量和傳統計算資源快速偵錯使計算過程得以做校正。在這個雜訊中等規模量子 (NISQ, Noisy Intermediate-Scale Quantum) 的年代₇由於量子位元之間的同調時間不長、量子閘保真度又不高的情形下不得不將邏輯量子位元與真實量子位元比例提高。而現在的量子位元系統缺乏主動回饋 (active feedback) 也就意味著目前的科技還沒辦法對一系列的量子位元做非破壞性的誤差測量、找到誤差來源、找到修正方法、也沒辦法在真實的量子位元生命期內修正錯誤。

 

既然目前真實系統帶的量子位元數量還不夠多，與其找到一個完整、嚴格的量子修正方法，在 NISQ 年代所需要的應該是減少誤差的技術，而其中一種方法是靠增加測量或事後選擇測量 (postselected measurement) 移除誤差₈。最終當然還是希望可以製造一台完全不會被物理性誤差影響的容錯量子電腦 (fault-tolerant quantum computer)，不過這種電腦至少需要長生命週期的量子位元、高保真度的量子閘和快速的回饋，每個都是具挑戰性的研究領域。

 

第一台量子電腦十之八九會是個連接傳統的中央處理器 (central processing unit 或 CPU) 的共處理機 (coprocessor) ，這種情形下電腦扮演加速演算法中特定部分的角色。在還沒找到誤差校正方法的這段期間內最被看好的演算法是量子傳統混合 (quantum-classical hybrid) 型的演算法，而這種演算法需要傳統和量子的處理器密切地配合，如此一來計算系統架構的設計也很可能會是傳統和量子混合組成。不過並非每個人都如此認為，就拿指令序列的設計來說，有些研究人員提倡指令序列的設計由量子和傳統指令混合_9,10，但也有人認為指令序列必須是純量子的₁₁。雖然近代的設計在電腦架構中加入共處理器增進效率已經非常地常見，但要怎麼在量子計算上使用混合架構依然是個待解的問題。

 

任何量子電腦的量子位元控制系統組成裡都免不了得將傳統電子元件整合進去，但連目前小型的量子位元系統都需要一層層的實驗室電子器材和一大堆的導線在低溫冷凍機或超真空室裡控制和操作量子位元，加上量子位元在真空室裡長時間地等待電子訊號傳送過來的時間本來就很容易有雜訊干擾；如果量子位元數量變多，晶載 (on-chip) 和輸出入的接線也會隨之增加，如此會使量子位元系統升溫並增加雜訊干擾。雖然目前的量子位元硬體裡每個量子位元只要用五到七條輸出入的電纜，不過這樣的設置除非有廠商做出更大的客製化稀釋致冷機 (dilution refrigerator)，不然量子位元的數量頂多就是幾十個而已。換句話說，量子位元控制系統的接線問題不解決就沒辦法使量子計算系統達到有用的規模。

 

不同的量子位元之間的連接排列方式和工程技術上的受限，例如控制線與量子位元的比例和量子位元的平行運作及選擇操控，也會造成更多運作上的限制。不過這樣的限制同時也提供了研究最佳化的機會，譬如英特爾實驗室 (Intel Labs) 證實了如果量子傅立葉轉換演算法的排程 (scheduling) 排得好，在近鄰連接 (nearest-neighbor connectivity) 的線性量子位元陣列 (linear array of qubits) 上的執行效率並不會比全連接 (all-to-all) 的量子位元系統差多少 (請見註解一)。

 

設計量子計算系統的關鍵是發展出一套包含許多小型演算法的函式庫，成為可以用在更大、更貼近量子化學和凝態物理等實際應用領域的基石。有了這些函式庫裡的演算法就可以從真實的量子位元出發進而設計出完整量子電腦系統，因為這樣的作法可以使研究人員瞭解真實量子位元要跑演算法時，各運算層所需要的功能並藉此設計相容的可擴展量子計算系統。即便還是有系統雜訊，這些小型的演算基石依然可以幫研究人員改進系統組織和架構，包含找到量子位元間的最佳連接法和適切的量子位元組織網格。只要量子閘的數量不多，研究人員就可以在沒有量子誤差校正的情形下用五到七個量子位元跑小型的演算法_12,13。如果特定應用區 (application area) 的演算法裡常用的子演算法都可以分開執行，那完整的量子演算法就有機會在量子位元數量增加、可執行的電路深度 (depth) 也增加地更大型量子位元系統上執行；而應用導向的設計就可以讓系統架構加速特定的應用區。雖然當更大型的量子位元系統出現後設計的難度也會跟著增加，但每次的量子電腦的硬體進步都讓研究人員從新一代的系統裡學到經驗也可以有系統地解決規模問題。

 

系統 ≠ 量子位元效能

過去在評量量子計算的效能幾乎都只著重在量子位元的部份，其中最主要的量化指標就是量子位元技術的物理特徵，譬如是否滿足迪文森佐準則裡量子位元同調時間的延長的部份以及量子閘的錯誤率、執行速率和連結度等效能表現。不過量子計算要從純物理研究轉型成電腦科技，研究人員應該開始將眼光放在整體系統效能，畢竟這才是使用者真正會在乎的。

 

從兩種不同量子位元技術的系統硬體架構對比研究14中雖然可以反應出硬體方面的一些狀況，不過這還是太過注重個別量子位元表現而忽略了對完整的量子計算系統也很重要的部份。現在量子計算已經漸漸地偏向如 IBM 的量子體積指標 (quantum volume metric) 同時考慮多種量子電路的系統效率指標₁₅，但是依然還有些課題需要被克服，譬如要制定一組同時兼顧根據小型量子位元系統上跑真實演算法的經驗並且可以使用在更大型量子計算技術的更廣用的系統效能指標。

 

當量子計算系統規模不再只是用少數量子位元跑小型演算法時，研究人員希望能將基本上已經完善的傳統電腦工程技術用來設計量子電腦將並將規模增大到可以跑更複雜的量子演算法。圖二列出了一些架構師在設計量子計算系統時必須兼顧的部份；其中演算法執行時間 (algorithm execution time) 代表的是在特定量子位元件和硬體上的量子位元平面編制 (qubit plane organization)  上編譯及做量子閘排程所需的資源；硬體控制和執行流程 (hardware control and excution flow) 裡包含了一組可用的量子閘，而平行性 (parallelism) 和傳統電子元件對個別量子元件的控制程度是決定系統效能的關鍵；量子位元效能指標 (qubit performance metric) ，譬如單和雙量子位元量子閘保真度、量子態供給與量測誤差和同調時間，這些都會影響系統的最大執行深度、錯誤容忍方法和其他系統效能特徵；量子位元平面編制則是指各個量子位元之間如何連接。如果量子位元平面所提供的是二維可平面化 (planar) 的近鄰連接，那就可能可以使用拓樸量子校正碼 (topological error-correction code) 做校正；但若無法得知系統的連接程度，那就必須要用重複碼 (repetition code) 或其他錯誤校正方法做校正，如此一來就會影響這個系統的錯誤容忍程度。

量子計算架構 ⇒ 新多學科領域

 

在傳統計算裡有些工具軟體可以拿來模擬系統裡所有元件的運作情形，包含系統的極限和限制，以製造更好的硬體設計。在硬體被實際製造出來之前其實都先用軟體模擬過各式各樣設計的系統效能，但量子計算裡的量子位元會有疊加態 (superposition) 和糾纏態 (entanglement) ，要製造系統效能模擬器是個奢求。更雪上加霜的是量子位元的物理性質會影響量子計算系統的運作，要怎麼找到量子位元網格的簡化哈密頓 (Hamilton) 使得放入系統效能模擬時能在運算時間和記憶體的限制下提供對系統足夠多的了解並不是件簡單的工作。

 

一個量子計算的系統效能模擬器基本上包含兩種類型的模擬：一種是系統模擬器，用來模擬軟體架構、硬體架構和編譯器到傳統脈衝等電子控制元件並且與第二種模擬器 ― 量子元件模擬器 ― 互動。量子元件模擬器負責少量量子位元系統的哈密頓與傳統控制界面的模擬。

 

第一種模擬基本上就是處理所有非量子部份的模擬，譬如程式語言、編譯器、控制方法和量子位元間的連接。這種模擬器可以回答一些量子計算架構的問題，譬如說：需要多少量子位元才能達到有用的程度？接下來一、二十年內量子計算架構可以支援到多少個量子位元？室溫和低溫控制的分界在哪裡？不同元素的架構是否必須用不同的量子位元製作？

 

第二種模擬器則是由少量量子位元的哈密頓組成。這個模擬需要將一些元件層級的指標列入考量，例如同調時間、單和雙量子位元閘的保真度、量子位元間與電磁波耦合的情形、量子位元的連接性和控制量量子閘的電子元件。因為量子位元通常是用多階 (multilevel) 的量子系統來近似，用少階的模擬器來做模擬時雖然不能把多出的高階都忽略掉但可以把他們當對系統的微擾。模擬器也要考慮將像半導體量子點的電荷捕捉 (charge-trapping) 缺陷當雜訊來看，如此一來研究人員就可以做一些像將系統上常用的量子演算法做最佳化、找出主要俱破壞性的雜訊來源和幫量子硬體除錯等工作。

 

如果能將兩種模擬器合併成一個整體的量子電腦效能模擬器的話能做的事情將會更強大。合併的量子模擬器就可以模擬特定的編譯器、量子位元控制系統、量子位元類型和量子位元間的連接方法的小型演算法運算情形，同時也能夠分析更改任意元件對於整體運算的影響，電腦架構師可以因此找到更好傳統或量子層面的設計。更進一步來說，實驗學家和量子位元設計師可以因此分析各種量子位元類型、連接狀態和控制上的限制進一步地理解他們的量子位元在整體系統下如何使用。

 

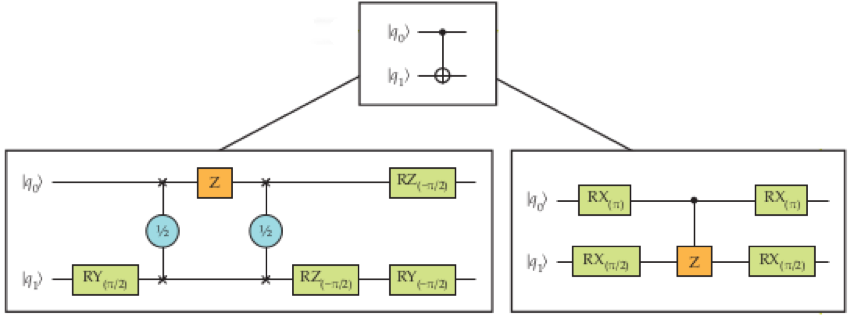
註解二詳細地列出系統效能測試可以如何幫助選擇系統層級的設計，這裡面展示了如何將一個常見的量子閘 ― 受控反閘（logical controlled-NOT gate 或簡稱 CNOT gate，如果第一個量子為元為 丨1 〉 則將第二個量子為元做一個 NOT 操作的雙量子位元閘) ― 用兩種方式拆解成為一個真實量子位元的操作和旋轉。對於特定的量子系統需要考慮不同的元素如量子位元同調時間、量子閘保真度、量子閘的執行時間長短和量子位元間的連接性找出最好的拆解方法。如果有一個可以模擬這種量子計算系統的模擬器就可以幫助做系統設計的決定。

 

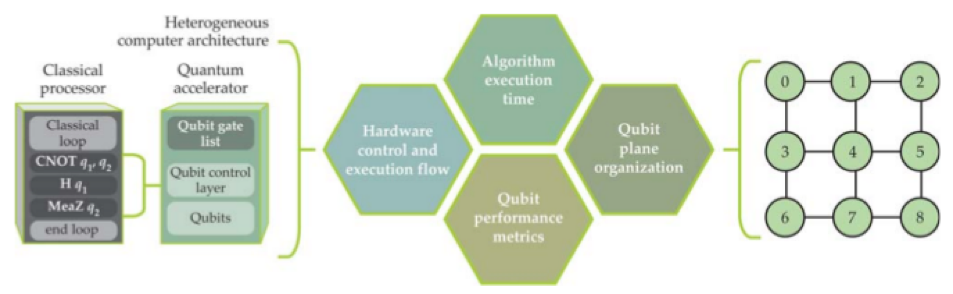
圖二、當研究人員在設計可以自動在真實量子位元元件上執行量子演算法的系統時會將相互影響的四種運作功能列入考量。譬如說右圖裡量子位元間的連接狀態會影響量子位元之間放在低溫系統裡的控制線數量、左圖則是顯示量子共處理機和傳統處理器之間的互動。

 

量子計算系統裡的古典尬量子的設計則需要由同時有物理和電腦架構背景的研究人員作選擇。這種量子計算架構的新領域已經準備變成新一代物理學家可以選擇的有趣職涯。這個領域打通了量子和傳統計算的疆界，而且將會是往後形成有用的量子電腦的關鍵。

 

作者們非常感謝 Jim Held 和 Xiang Zhou 的貢獻。

 

 

註解一、設計比一比：量子傅立葉轉換

左下方圖是順序由左向右的量子電路，圖裡每條線都對應到一個特定的量子位元，其中每個方框都代表著一種操作。量子閘上的符號代表該作用在該量子位元上各種不同的么正操作 (unitary operation)。量子閘是量子電路中的最基本的組成，其重要性就如同傳統計算裡數位電路中的邏輯閘一樣。下面的圖表描述的就是量子傅立葉轉換 (QFT, quantum Fourier-transformation) 的演算法。這裡的 H 代表的是阿達馬閘 (Hadamard gate)，這是將一個量子位元的丨0〉和丨1 〉態旋轉成他們的疊加態，將丨0 〉轉到丨0〉+丨1 〉而丨1 〉到 丨0 〉-丨1 〉，用矩陣表現時就是
 

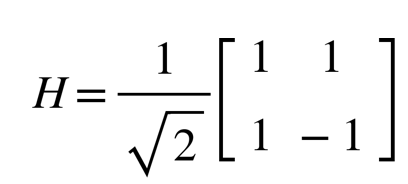
而受控相位偏移閘 (controlled phase gate) C-Pn 也是作用在兩個量子位元上，如果兩個量子位元都同時在丨1 〉的態上則做一個相位的改變：
 

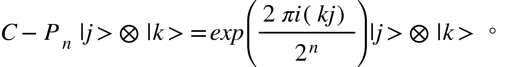
互換閘 (SWAP gate，電路圖裡最右邊的垂直線) 則是負責將兩個量子位元的態互相交換。

 

 

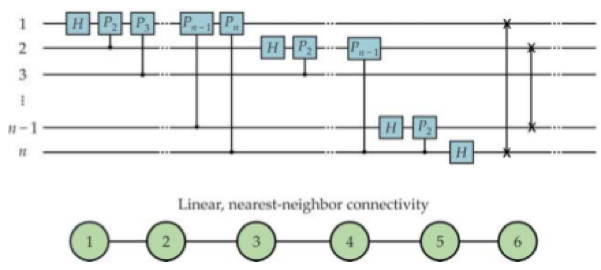
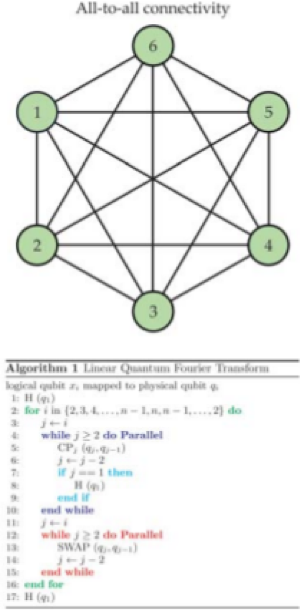
一個執行 n 個量子位元的量子電路所需要的量子閘大致上會是 O(n2) 的數量級，而 O 這個符號可以用輸入資訊量與所需要的運算時間或空間關係將演算法分類。不過如果所有的量子位元都連接在一起如下方右圖所示，理論上來說最佳的運算方法應該會是 O(n) 的電路深度(circuit depth，一個演算法從輸入到輸出最長的路徑或說是最多的運算步驟)。綠色的圈代表的是個別的量子位元，而黑線連接起來代表這兩個量子位元之間可以做一個雙量子位元閘的操作。實際上比較容易製造的系統是如下方左圖所示的量子位元線性陣列，其中只有最靠近的量子位元間有連接。讓人訝異的是 QFT 就算是在線性陣列的量子位元系統上的排程電路深度也可以是 Ｏ(n) 的數量級，與全連接的量子位元系統相比指多出小小的 0.25 倍運算量 (細節請參閱 A. Holmes et al., https://arxiv.org/abs/1811.02125 的文章)。最右下角的圖是這個演算法的偽碼 (pseudocode) ，其中外迴路需要執行 n 次，而外迴路裡還有兩個可以平行運算的兩個迴圈，也就是說這個是 O(1)  的時間長度。這樣子的演算法設計也可以把最後那個互換閘的步驟拿掉。

 

 

註解二、選擇受控反閘的拆解方法

受控反閘是一種產生糾纏的操作，假如控制位元是 1 的態，那目標位元的 1 和 0 做交換。要在特定系統裡使用量子閘必須被先將它拆解成一系列的該量子位元技術的天然閘的操作。這裡提供兩種可能的拆解方法，圖裡的RX、RY 和 RZ 分別代表對 x、y、z 軸的轉動。系統效能模擬可以提供一些指標幫助選取在特定系統裡選擇哪種受控反閘拆解方式最合適。

 

根據單或雙量子位元量子閘的保真度和運作速度，研究人員可以選擇其中一種拆解方式當作該系統的受控反閘的操作。不過並非一種拆解方式永遠都比另一種好，有時在執行演算法的特定部份時也會因顧及可用量子位元的效能而選擇另一種拆解方式
 

 

參考資料

1. D. P. DiVincenzo, Fortschr. Phys. 48, 771 (2000).
2. A. Montanaro, npj Quantum Inf. 2, 15023 (2016).
3. R. Van Meter, C. Horsman, Commun. ACM 56, 84 (2013).
4. F. Chong, D. Franklin, M. Martonosi, Nature 549, 180 (2017).
5. N. C. Jones et al., Phys. Rev. X 2, 031007 (2012).
6. M. Oskin et al., in Proceedings of the 30th Annual International Symposium of Computer Architecture, ACM (2003), p. 374.
7. J. Preskill, Quantum 2, 79 (2018).
8. J. I. Colless et al., Phys. Rev. X 8, 011021 (2018).
9. R. S. Smith, M. J. Curtis, W. J. Zeng, https://arxiv.org/abs/1608.03355
10. A. W. Cross et al., https://arxiv.org/abs/1707.03429
11. A. JavadiAbhari et al., in Proceedings of the 11th ACM Conference on Computing Frontiers, ACM (2014), art. no. 1.
12. N. M. Linke et al., Phys. Rev. A 98, 052334 (2018).
13. J. S. Otterbach et al., https://arxiv.org/abs/1712.05771
14. N. M. Linke et al., Proc. Natl. Acad. Sci. USA 114, 3305 (2017).
15. L. S. Bishop et al., Quantum Volume, IBM technical report (4 March 2017), available at https://pdfs.semanticscholar.org/650c/3fa2a231cd77cf3d882e1659ee14175c01d5.pdf

 

本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於Physics Today, January 2019 雜誌內(Physics Today 72, 3, 40 (2019);https://physicstoday.scitation.org/doi/full/10.1063/PT.3.4163)；原文作者：Anne Matsuura 、Sonika Johri、Justin Hogaboam 。中文編譯：朱家誼博士，國立中興大學物理系博士後。

Physics Bimonthly (The Physics Society of Taiwan) appreciates that Physics Today (American Institute of Physics) authorizes Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by Anne Matsuura , Sonika Johri, Justin Hogaboam , and is published on https://physicstoday.scitation.org/doi/full/10.1063/PT.3.4163 The article in Mandarin is translated and edited by Dr. Chia-Yi Ju, working on Department of Physics, National Chung Hsing University.