來自布魯日的奇人: 西蒙· 史蒂文(下) 低地國的文藝復興全才

上一回阿文介紹了在荷蘭獨立戰爭扮演軍師角色的萬用學者，西蒙·史蒂文。其實他的貢獻不限於軍事，他多才多藝，稱得上是個標準的「文藝復興人」。（Renaissance man，或拉丁語的Homo universalis，意思與「通才」(polymath)相近，但通常指的是在藝術或科學方面。這個詞語的來源是在文藝復興時出現了不少這類的人物，最有名的像是巴迪斯蒂·阿伯拉蒂（Leone Battista Alberti，1404年－1472年，身兼建築師、建築理論家、作家、詩人)和李奧納多·達·文西就是當中的佼佼者。現今「文藝復興人」一詞泛指「對多方範疇感興趣，或對多方範疇有所成就」的人。)  西蒙·史蒂文的成就，就讓阿文我一樣一樣數給您聽:

算術 

史蒂文在歷史上最為人稱道的就是引進十進位小數。他在1585年出版了La Thiende，這本長達29頁的小冊子介紹了基本的小數部分。他寫這本小書的目的是給：...觀星者，測量師，地毯製造者，釀酒師，造幣廠長和各種商人。
 

 
By Patrick87 - Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=33047242

史蒂文在十分之一的冪次冪的指數上畫了一些小圓圈。 他打算用這些圈起來的數字來表示是指數，他的符號如今看起來很笨拙。將整數與十進制小數點分開的點似乎是德國學者Bartholomaeus Pitiscus (1561 – 1613) 的發明，在其三角表（1612）中出現了該點，並被蘇格蘭學者John Napier在他的對數論文（1614和1619）中所採用。

曾經有人認為史蒂文發明了十進制小數，但是後來的研究發現，中世紀的伊斯蘭學者al-Uqlidisi早在952年的一本書中Kitab al-Fusul fi al-Hisab al-Hindi (The Arithmetics of Al-Uqlidisi)這本書中引入了十進制小數。此外，十進制小數的系統發展是在1427年由波斯學者Al-Kashi撰寫的《 Miftah al-Hisab》一書中也早就被使用。但是無庸置疑地，史蒂文是讓十進位小數在西歐開始被廣泛使用的關鍵人物。


儘管史蒂文沒有發明小數點，但他的確在歐洲引入了小數點的用法。史蒂文指出，普遍採用十進制硬幣，度量衡和重量只是時間問題。實際上，這要等到法國大革命以後才實現。不過很快地，羅伯特·諾頓（Robert Norton）於1608年在倫敦出版了《 La Thiende》的英文譯本。該書的標題為Disme，《十分之一的藝術》或《十進制算術》，正是這本英譯本啟發了湯瑪斯·傑佛遜（Thomas Jefferson）為美國提出了十進制的貨幣。時至今日，美金一角還是叫做 Dime。


同年（1585年），史蒂文也出版了La pratique d'arithmétique和L'arithmétique《算術》，這是他少數幾本用法語撰寫的書。在《算術》，史蒂文提出了一種統一的方法來求解二次方程式，該方程最初由印度的布拉瑪古普（Brahmagupta）先前記錄了將近一千年。史蒂文在他的書Stelreghel中還使用了+，-和√這些現代算數常用的符號。尤為重要的是史蒂文也接受負數。他還強烈地要求將所有的數字（例如平方根，無理數，，負數等）的本質都是相似的，不應該像古希臘數學家(像是畢達哥拉斯)那樣獨尊整數。史蒂文的實數概念基本上為後來的科學家所接受。根據數學史家范德瓦爾登(Bartel Leendert van der Waerden 1903-1996)的說法，史蒂文消除了“將數字侷限在整數（如歐幾米德所主張）或對有理分數（如丟番圖Diophantos所主張）的想法……實數形成了一個連續統一體。他的實數一般概念”明確地由後來的所有科學家”所接受了 。這對笛卡爾發展出解析幾何也大有幫助，笛卡爾年輕時就在莫里斯的軍隊中當兵呢。

 
繪圖

史蒂文在《 Problemata geometrica幾何問題》（1583年）中提出的幾何學主要還是基於傳統的歐幾里得和阿基米德的結果，但他研究的問題表明他也受到了德國畫家杜勒的影響。 他使用相似性的概念研究多邊形和多面體相關的問題，並且也針對正多面體和半正多面體展開研究。(半正多面體是泛指所有具有對稱群且由2種或2種以上正多邊形所組成的多面體，其中包含13種阿基米德立體阿基米德立體的每個頂點的情況相同，邊均有相同長度)。這本書也是他的唯一一本以拉丁文出版的書。 後來他大力倡導用荷蘭語撰寫科學著作，並在1586年撰寫的文本中明確指出為何使用荷蘭語的原因。

儘管史蒂文從年輕就開始從事數學工作，但他收集了他的一些數學著作，這些著作要等到1605年至1608年間才結集成Wiskonstighe Ghedachtenissen （數學回憶錄拉丁語：Hypomnemata Mathematica）中出版。其中包括他較早的著作，例如De Driehouckhandel（三角學）、De Meetdaet（測量實踐）和Deursichtighe（觀點）並由他編輯並出版。De Driehouckhandel是三角學的重要著作。史蒂文在有關投影的基本定理和新定理都有貢獻，以他為名的定理在著名數學家的數學著作中都找得到。投影是伴隨著文藝復興發明的透視法在藝術與工程的應用而為人所注意。史蒂文在製作透視圖方面有許多創新，例如計算在不垂直於地面的畫布上繪製圖紙的透視圖的情況，以及反向透視的情況。反向透視如果給出了一個對象和該對象的透視圖，如何回推計算觀察者的眼睛在哪裡的問題。不過射影幾何後來發展成了一個龐大充實的學科，這是史蒂文難以想像的。

力學
史蒂文另一個擅長的領域是力學。他在稱重技術的第一本書中，第二部分：命題[斜重的性質]，第41頁，定理XI，命題XIX，他得出了力平衡的條件。(如下圖)將均勻分佈的念珠串，放在兩個斜面上，他推論兩邊念珠串的重量的比例如果與斜面長的比例相同的話，念珠串保持靜止，形成靜力平衡。

史蒂文做一個假想實驗，將念珠串連成一個環。如果這樣放念珠串會往任何一個方向移動，那麼這個運動會一直持續下去。如此一來，不花任何力氣，就能讓念珠串一直轉動，史蒂文直覺地認定這是不可能的。這個結論也可以表示成兩邊念珠串的重量乘以三角形的高度除以邊（邊相對於水平面的角度的正弦值）要相同才會平衡。這個概念的證明圖被稱為“史蒂文努斯的墓誌銘”(Epitaph of Stevinus)。

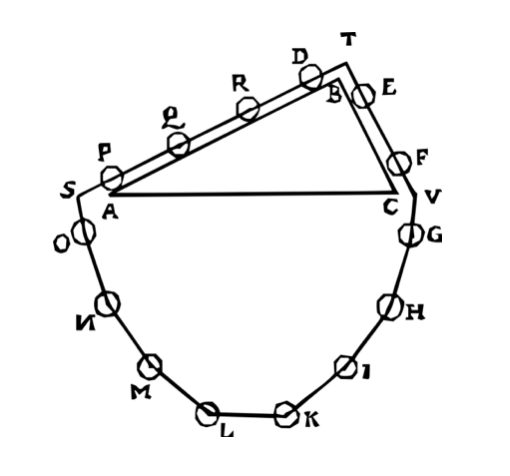
By Tos - http://www.dbnl.org/tekst/berk003voet01_01/berk003voet01_01_0002.htm, Public Domain, https://commons.wikimedia.org/w/index.php?curid=3868594

 
正如荷蘭科學史家迪克斯特豪伊斯(E. J. Dijksterhuis 1892-1965)指出的那樣，史蒂文關於傾斜平面上平衡的證明利用歸謬法證明了永動機是不可能的。迪克斯特豪伊斯說，史蒂文“明確地利用了能量守恆定律……遠在它被明白表述之前”。

史蒂文對靜力學頗為拿手，他比皮埃爾·瓦里尼翁（Pierre Varignon 1654 – 23 1722)）還早就展示了利用力的平行四邊形將力加在一起。此外他還把穩定與不穩定的平衡區分開來，也曾對滑輪系統進行了科學研究。身為工程師的他自然對液壓問題也不陌生。他發現液體中的壓力與容器的形狀和底部的面積無關，而僅取決於其高度，並且壓力與包含液體的容器的形狀無關。他還給出了測量船舶側面任何給定部分壓力的方法。這些工作算是1653年法國科學家帕斯卡發現的帕斯卡定律的前驅。


除了這些衍生於實際工程問題的物理成就以外，史蒂文還有一項令人詫異的壯舉。他在1586年，他證明了兩個重量不同的物體以相同的加速度掉落。據說他是與Jan Cornetts de Groot 兩人將一對尺寸相同的鉛球載運到台夫特的新教堂（Nieuwe Kerk, 1496年完成）的頂部，然後把它們扔到下方30英尺處的木製平台上；而其中一顆球比另一顆重十倍。球掉落後，兩顆球基本上同時擊中下方的木製平台，這表明相同大小之物體是以相同速度落下，與物體的質量無關。因此，史蒂文斷定，亞里斯多德理論是錯的。不過由於缺乏精密的計時儀器，他們的實驗似乎是定性而非定量的。史蒂文在1586年的著作《De Beghinselen Der Weeghconst》（該書可譯作《靜力學原理》和《平衡器原理》）中發表了他的結果。順便一提，跟他做這個實驗的正是與他一起改良風車的夥伴。

天文

在十六世紀後半葉到十七世紀初，哥白尼系統還沒有普遍被接受，但是史蒂文在1608年出版的《德赫默洛普(De Hemelloop)》中強烈捍衛了哥白尼的太陽中心系統。雖然他嘗試進一步解釋行星的運動，但沒有成功。倒是他在1608年的《潮起潮落理論》中主張月球的吸引力是潮汐的起因，並強調需要做進一步的研究。這一點比約翰內斯·克卜勒（Johannes Kepler）還早一年，克卜勒在1609年也提出月球的引力會引起潮汐。反觀伽利略（Galileo Galilei）在他的1632年出版的「關於兩個主要世界體系的對話」中，試圖將潮汐歸因於地球繞太陽運動引起的水的晃動。他希望潮汐可以提供地球運動的力學證據。這是錯誤的，當有人跟伽利略表示如果他的理論是正確的話，一天只會發生一次漲潮，但實際上一天會發生兩次，伽利略居然回說那是亞得理亞海的地形特殊！不過第一個正確又完整地解釋潮汐現象的是牛頓。他對潮汐（及許多其他現象）的解釋發表在《原理》（1687）中，並用他的萬有引力理論解釋了月球和太陽引力是潮汐產生力的起源。

音樂

史蒂文未完成的手稿（Van de Spiegheling der singconst）（寫於1605年）在他死後於1884年出版，裡頭提到了十二平均律。無獨有偶地，中國明代音樂家朱載堉(1536－1611，他是鄭王的嫡長子，朱元璋的八世孫，但是他執意不當王爺，把王位讓給堂弟。)在萬曆十二年（1584年）首次提出「新法密率」（見《律呂精義》、《樂律全書》），推算出以比率2的12次方根將八度音等分為十二等分的算法，並製造出十二平均律律管及律準，是世界上最早的十二平均律樂器。義大利的物理學家伽利略·伽利萊的父親溫琴佐·伽利萊(Vincenzo Galilei,1520-1591)曾試圖解決十二平均率問題，但他用的倍率是18:17，自乘12次後只得1.98556，不是2，他的系統只可算近似十二音階平均律。史蒂文與朱載堉一樣採用2的12次方根，但是因計算精度不夠，他算出的弦長數字，有些偏離正確數字一至二單位之多。(全音程設為一千)。當然史蒂文與朱載堉都不知道彼此的存在，也算是一樁奇譚。至於大家熟悉的巴哈《平均律鍵盤曲集》的「平均律」一詞並非十二平均律，而是指而「合適、妥當的調律」。各位也許會覺得史蒂文怎麼連音樂都涉獵?其實自古典時期以來音樂，天文，幾何，算術合稱四藝(quadrivium，意為四條道路）。其他三個領域，史蒂文都有貢獻，所以他懂音樂，一點也不足為奇。

簿記

史蒂文出版的第一本書是《利率表（Tafelen of Interest）》（利率表，1582年），在西歐，這是第一次公開了利率表。在此之前，只有手稿可用，而且還可以用很高的價格賣給了商人，商人和銀行家。史蒂文還將複式簿記(double-entry bookkeeping，簡稱DBE)帶入荷蘭的共和國軍隊中，因為他年輕時是安特衛普的書記員。但是，史蒂文也建議在一般國民家庭中使用這種新式簿記的人。史蒂文也曾撰寫了有關會計的創新論文。毫無疑問，簿記知識的傳播注入了荷蘭統治階級和政治精英的思想。正如歷史學家雅各布·索爾（Jacob Soll）所指出的那樣：“ 貿易與商業是城市日常生活的重要組成部分，是州政府的重要組成部分。荷蘭統治精英熟悉金融，工業和貿易的細節。’

建築

史蒂文晚年著有一部未完成的城市與建築理論著作 De Huysbou （建築論），由他的後人集結整理出版，這本書內容涉及建築設計、軍事工程與城市規劃等方面的理論。就城市邊界輪廓而言，當時普遍認為星形城市防禦較優越，但史蒂文獨排眾議，企圖提出兼具防禦與秩序格局的方形城市輪廓。他也主張城市公共建築要整合類似機能的設施進行規劃，並配置在各自適當的地方。可惜史蒂文未能及時完成此書。他在1620年去世。此後，這篇遺稿的片段散佈在君士坦丁，克里斯蒂安·海更斯和以撒·貝克曼等學者之間。艾薩克·貝克曼（Isaac Beeckman）的日記中包含片段，他的兒子亨德里克（Hendrik）在他1649年出版的《Burgherlicke Stoffen材料政治學》發表了一部分。。

荷蘭文

史蒂文與當時其他的「文藝復興人」最大的不同是，他並不像其他人獨尊拉丁文，反而認為荷蘭語才是科學寫作的絕佳語言，因為正如他憑經驗用該語言講的單音節單詞比他所比較的任何（歐洲）語言都可以表示更多的概念。 這就是為什麼他用荷蘭語寫所有作品，而把它們的翻譯留給別人去做的原因之一。另一個原因是，他希望他的作品對那些還沒有掌握當時通用科學語言（拉丁語）的人們使用。史蒂文認為科學語言與工匠語言一樣重要。他將許多數學術語翻譯成荷蘭語。多虧了史蒂文的堅持，荷蘭語才有了許多科學詞彙，例如數學的“ wiskunde”（眾所周知的或確定的藝術），“ natuurkunde”（“自然的藝術”）用於物理學；“ scheikunde”（“分離藝術”）用於化學；“ sterrenkunde”（“恆星藝術”）用於天文學；“ meetkunde”（“測量藝術”）用於幾何學。他發明的一些詞後來產生演變：“ aftrekken”（減法）和“ delen”（除法）保持不變，但隨著時間的流逝，“ menigvuldigen”變成了“ vermenigvuldigen”（乘以，添加的“ ver”強調了這是一個事實） ）。 “ Vergaderen”成為“ optellen”（添加）。


史蒂文在光學，地理，天文學，的許多著作後來都被萊頓大學的數學教授斯涅耳（Willebrord Snell, 1580-1626）翻譯成拉丁文。斯涅耳比史蒂文小一個世代，本身是一位傑出的數學家。1621年，他重新發現了折射定律，因而命名為斯涅耳定律。但是，他並沒有主動地將這定律發表出來。後來，於 1703年，克里斯蒂安·海更斯在著作《Dioptrica》中談到這定律，才正式地將這定律的發現歸功於他。斯涅耳還改進了用多邊形計算π的近似值的傳統方法，他在Cyclometricu（1621）中發表了該方法。 使用他的方法，有96個面的多邊形可將圓周率算到小數點下7位，而舊的方法僅到小數點兩位。 他的老師範·科倫（Van Ceulen）後來改進了他的方法，一口氣算到小數點下35位!


斯涅耳還有一項創舉，1615年，他想出一種方法來測量地球半徑。應用三角測量方法 (trangulation method) 來測量同經度兩個地點之間的距離，就可以計算出地球半徑。發表於1617年，他的著作《Eratosthenes Batavus》（巴達維亞的埃拉托斯特尼，巴達維亞是低地國的古稱）專門描述這方法。緯度相差一度的兩個荷蘭小鎮阿爾克馬爾和 Bergen op Zoom 之間的距離，他測量出是 107 公里。將這數值乘以 360 ，他估計地球圓周為 38,520 公里；實際圓周大約為 40,000 公里。斯涅耳算是介於史蒂文與海更斯之間的傑出人物。
 

雖然莫里斯親王(他的長兄於1618過世，他程為奧蘭治親王)希望繼續對西班牙的戰爭，但是，當西班牙實質上承認聯合行省擁有獨立主權的時候，繼續進行戰鬥的熱情就變小了。1609年莫里斯與西班牙終於談成了停戰協議，聯合行省共和國算是站穩了腳跟，史蒂文肩上的重任也終於得以卸下。他在1612年在海牙的Raamstraat買了房子，價格為3800荷蘭盾（這是他地位和財富很高的另一個標誌）。他的妻子名叫凱瑟琳·克萊（Catherine Krai），他們育有兩男兩女，分別是弗雷德里克（Frederic），亨德里克（Hendrik），蘇珊娜（Susanna）和列維娜（Levina）。 他們的第二個孩子亨德里克（Hendrik）後來成為著名的科學家，日後編纂了西蒙的文集。當史蒂文於1620年過世時，莫里斯在兩年前已經將原先的盟友，後來翻臉成了政敵的大議長，奧爾登巴內費爾特逮捕並斬首，自己成了共和國的實質的惟一領袖，而日耳曼也陷入了全面性的新教與天主教的戰爭，但是荷蘭相對地還是享受著和平的生活，直到1621年荷蘭與西班牙戰火再起，當時史蒂文已經過世了。1625年莫里斯親王也過世了，共和國由莫里斯的弟弟弗雷德里克·亨德里克（Friderik Hendrik，1584－1647）領導繼續戰鬥。弗雷德里克·亨德里克具有傑出的軍事才能，他在與西班牙的決定性鬥爭中為尼德蘭作出了巨大貢獻。他於1625年開始領導全部聯省共和國軍隊，投入三十年戰爭。這支軍隊先後攻陷了西班牙統治的赫龍洛（1627年）、斯海爾托亨博斯（1629年）、馬斯垂克（1632年）、布雷達（1637年）、根特（1644年）、胡斯特（1645年）；為了迫使西班牙讓步，弗雷德里克·亨德里克於1635年與法國結成同盟。他領導準備與西班牙簽署最後和約的工作。由於弗雷德里克·亨德里克的努力，尼德蘭最終實現了與西班牙締結尼德蘭-西班牙和約（1648年1月），結束了八十年戰爭，荷蘭正式獨立（三十年戰爭也在同年結束）。弗雷德里克·亨德里克在條約正式簽訂前就過世了，共和國的執政由他的兒子威廉二世繼承。這時臺灣已經是荷蘭東印度公司的領地二十四年了。


多才多藝的史蒂文雖然不像其他的”文藝復興人”像是達文西，帕斯卡，歌德或是萊布尼茲那樣地有名，然而他優游於技術與科學之間，卻也別樹一格。他大力推廣科學用的荷蘭語這一點，令人覺得有趣。比起其他幾位”文藝復興人”，史蒂文似乎更像是荷蘭的獨立英雄，不僅在政治上，軍事上獨立，更是在學術上，思想上走出一條自己的路，這實在是令人佩服得五頂投地呀!這樣的奇人，令阿文我心嚮往之!大丈夫亦若是，您說是不是?


參考資料:
(一)中文 英文 荷文維基相關條目https://weaponsandwarfare.com/2019/03/23/simon-stevin-c-1548-1620/
(二)https://en.wikisource.org/wiki/1911_Encyclop%C3%A6dia_Britannica/Stevinus,_Simon
(三)O'Connor, John J.; Robertson, Edmund F. (January 2004), "Simon Stevin", MacTutor History of Mathematics archive, University of St Andrews.


延伸閱讀：
來自布魯日的奇人: 西蒙·史蒂文(上) 荷蘭獨立戰爭的諸葛孔明