探索量子與古典間的灰色地帶
- 物理專文
- 撰文者：陳宏斌
- 發文日期：2019-12-05
- 點閱次數：1562
逐漸逼近古典極限
隨著各項技術的發展與應用需求的快速成長，尤其是在大數據處理與人工智能等領域崛起的現今，對於高速運算能力的仰賴與日俱增。目前在業界提升運算能力的方法，都是基植於電晶體電路體積的微縮以達到數量與密度上的提升。然而，由於原子的體積自然地定義了一個極限尺度，這種競逐微縮化的過程，終將停止於這個終點線前，無法跨越自然界所設下的這堵高牆。這個問題的根本在於，當元件設計地如此細小時，許多量子的特性便會凸顯出來甚至主導了元件的行為，這使得科學家與工程師們不能再以古典物理的框架來研究設計這樣的元件，否則無法獲得良好的解釋與行為預測。著眼於對未來發展的洞見，元件系統的各種量子特性的深入研究與量化勢在必行。成功大學的研究團隊攜手與來自日本理化學研究所 (RIKEN)、韓國高等技術學院 (KAIST)、交通大學的學者們，共同組成研究群組，探討量子系統的消相位過程與亂序環境影響下的關係，最新研究成果發表於2019年8月22日《Nature Communications》期刊 [1]，且其先導研究也於2018年1月19日發表在《Physical Review Letters》期刊 [2]。
駕馭量子的力量
而在另一方面，若能善用這些奇特的量子特性，也能夠開闢出一條有別於以往的途徑。量子電腦與量子資訊科技就是跳脫了古典物理的框架，建立在量子物理的基礎上而誕生 [3]。量子電腦透過運用量子的特性，達到強大的平行運算能力，可以在極短的時間內完成一般古典電腦難以解決的問題，被認為是下個世代的新興運算工具，並且吸引了全球學界與業界競相投入。而量子電腦之所以擁有強大的運算能力，其關鍵在於量子元件系統可以處於量子疊加態 (Quantum superposition) 以及不同量子元件系統之間可產生量子關聯性如量子糾纏 (Quantum entanglement) 等。在傳統電腦裡，數位化的資料是用二進位運算方式的位元 (Bit) 做為最基本的儲存單位，每個位元的狀態只能處在0或1。而儲存量子資訊最基本的單位則是量子位元 (Quantum bit, qubit)，量子位元可以處於任何 |0〉與 |1〉的疊加態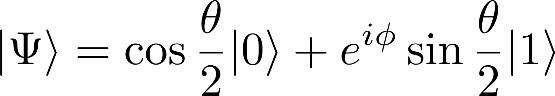
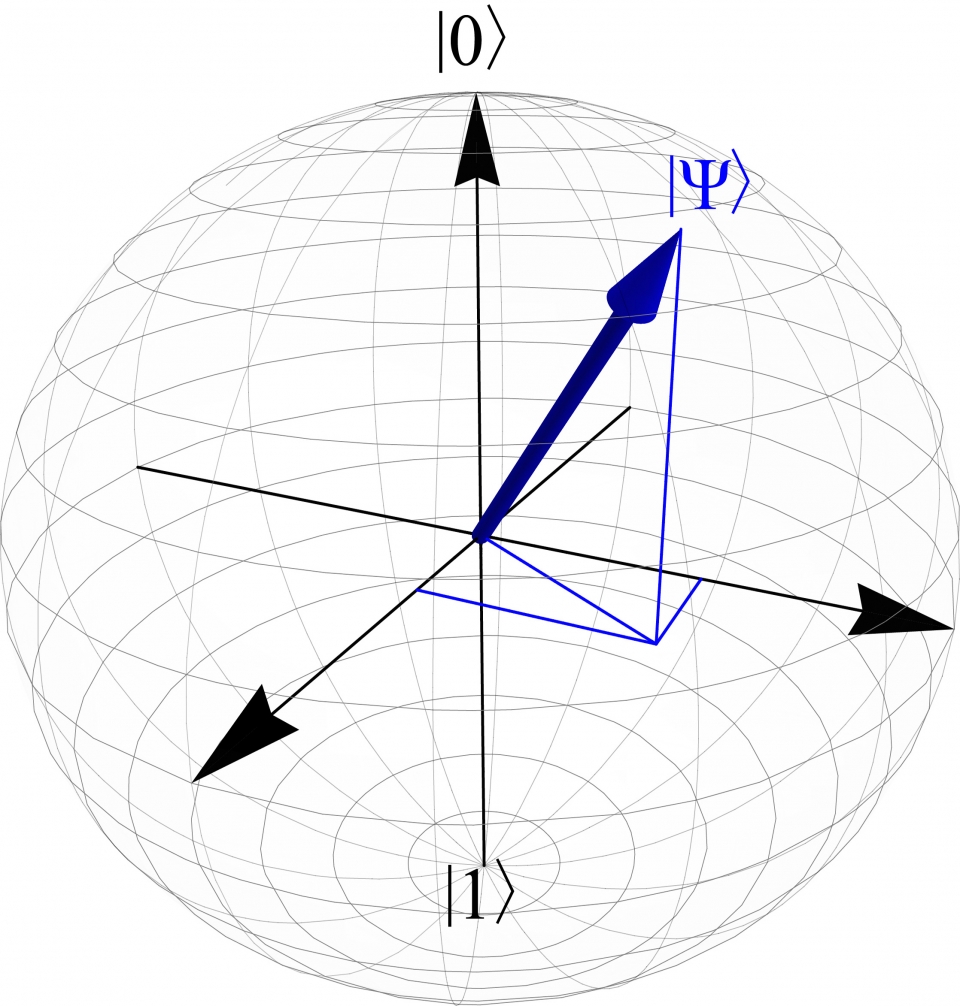
我們也常使用布洛赫球 (Bloch sphere) 這樣的幾何的方式幫助我們圖像化地了解量子態的空間 (見圖一)。因為疊加態的特性，一方面大大擴充了資訊可能儲存的空間，同時也使得量子平行運算成為可能。此外多個量子位元之間所建立起的量子關聯性也是非常重要的量子運算資源，透過不同的手法來操作量子關聯性，可以使得量子資訊能在各個量子位元之間傳遞，甚至可以做到高效的量子遠距傳輸 (Quantum teleportation)，或是隔空操縱 (Quantum steering) 遠方的量子位元，這都是以往的古典電腦所辦不到的。
技術瓶頸
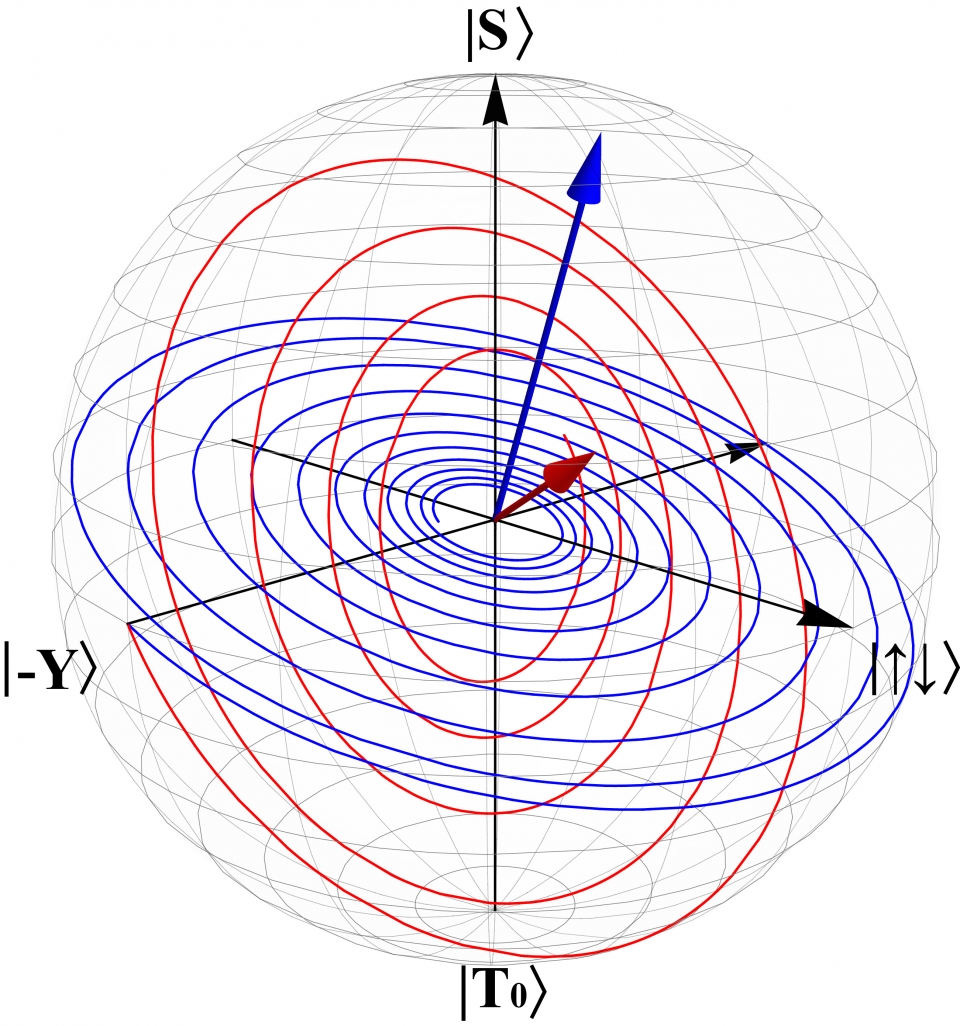
儘管擁有種種強大的能力與發展願景，量子電腦至今多半還是只侷限於在實驗室內運作，距離商用化還有一段路要走。其中一個最大的技術瓶頸在於，這些特殊的量子特性十分脆弱，很容易因為周圍原子環境的破壞而消逝殆盡。例如半導體量子點中，困陷於位能阱中的電子必須承載在由原子構成的晶格結構，因此無可避免的會與周圍的原子交互作用，尤其是其自旋對於周遭原子核自旋產生的磁場漲落就相當敏感，當電子自旋態製備在某個量子疊加態後，基底之間的相位差會因為周遭的磁場漲落導致其時間演化逐漸變得模糊不確定，最後完全衰退消失，這個過程稱之為消相位。如圖二所示為一對電子形成單態-三態量子位元 (S-T0 qubit) 後，與原子核產生超精細交互作用因而發生不同頻率的消相位過程。量子位元一旦歷經了消相位過程，便失去了量子疊加態的特性，行為將會變的與古典電腦的統計特性一致，因此消相位過程被認為是量子到古典過渡的一個主因 [4-7]。同樣的，這個消相位過程也會破壞多個量子位元之間的量子關聯性，使得量子電腦不再具有量子的特性，因而無法發揮應有的效能甚至頻頻出錯，這樣一來運算效能便大打折扣。因此，深入探討這些消相位機制以及檢測量子性質是否還能持續保有，在提昇量子電腦的效能上是至關重要的課題。猶如現代電子產品在生產的過程中，為確保其產品品質，需要一些品質檢測的程序。
量子性的檢測
那麼，該如何檢測一個量子元件是否還保有量子特性？由於量子元件都相當的微小，任何的直接觀測都會影響到元件的量子態而導致量子態塌縮的發生，如此一來該量子元件就被損毀而不再處於起初欲檢驗的狀態了。因此在量子資訊理論裡，常會使用古典策略模擬的方法。我們首先來看兩個最典型的例子。
第一個例子是光子場量子性的檢測，當給定了一個光子場以及其密度矩陣 ρ 之後我們會透過一些轉換方程將其轉換成Wigner function [8]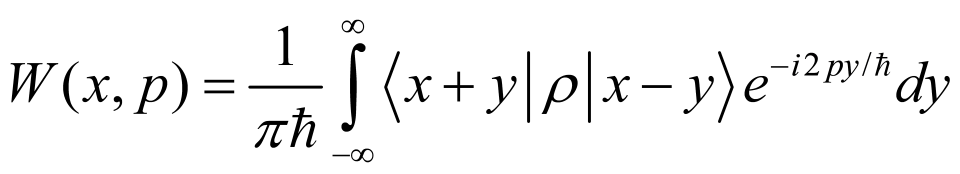
或是Glauber-Sudarshan P representation [9, 10]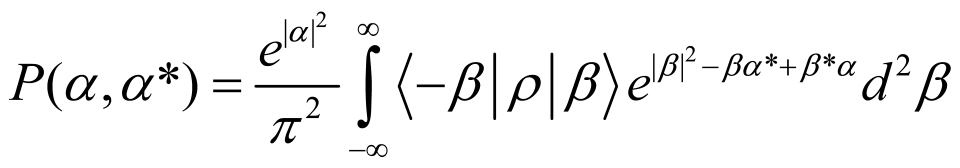
其背後的原理源自於古典物理的相空間表示法。在古典物理中，一個物體的位置及動量可同時被測定，因此以位置及動量做為坐標軸構成所謂的相空間，古典物理便使用分布在相空間中的機率分布來描述物體的行為。借用這樣的概念，Wigner function就是將一個光子場的量子態轉換到相空間，得到相空間中的準機率分布函數。有時候我們會遇到Wigner function出現負值機率甚至奇異點的情況，這些古典物理中不會出現的行為，便是光子場 ρ 的量子特性的展示，因其所包含的負值機率的行為，不能再用古典的方式去考慮。G-S P representation也是類似的概念，只是改成以同調態 (coherent state)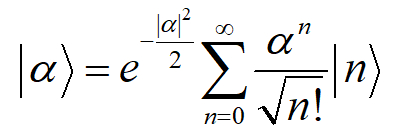 
做為相空間的座標軸。這兩個函數都是準機率分布函數，一旦出現負值機率的情形，就驗證了該光子場具有良好的量子特性，而不存在任何古典物理中的類比。
第二個例子是二體量子關聯性的檢測，這在量子資訊理論裡尤其重要，常用一個臆想實驗來說明。假設愛麗絲與鮑柏兩人分隔兩地進行實驗，每回合實驗開始後，他們就會共享一對量子位元，但他們僅能操作他們自己手上的量子位元或者以電話互相通知對方操作的結果 (LOCC)。實驗的目的是要確認愛麗絲與鮑柏所共享的量子位元對之間是否存在著量子關聯性。實驗的進行方式是，每當兩人收到各自的量子位元後，他們便各自選擇某個方向的基底進行測量，接著與對方電話通訊，紀錄彼此的量測方向和量測結果。在重複進行多回合這樣的實驗後，他們就可以完成一份量測的統計表。若這份統計表可以用一組局域隱變數模型 (Local hidden variable model)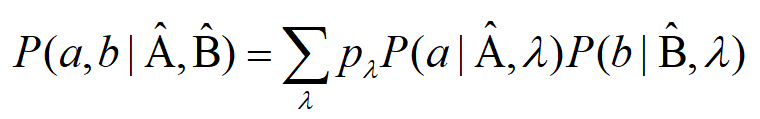 
重現，那麼愛麗絲與鮑柏便會認為他們共享的這對量子位元對的行為可以用古典的方式，亦即實在性 (Reality) 與局域性 (Locality)，來描述，他們因此無法相信這對量子位元對具有足夠強的量子關聯性。反之，如果他們發現統計表違反了貝爾不等式 (Bell inequality)[11]，那麼上述的古典描述法與局域隱變數模型便不可能用來規範這對量子位元對的行為，因此愛麗絲與鮑柏才能相信其具有良好的量子關聯性。
哈密頓量係綜集合
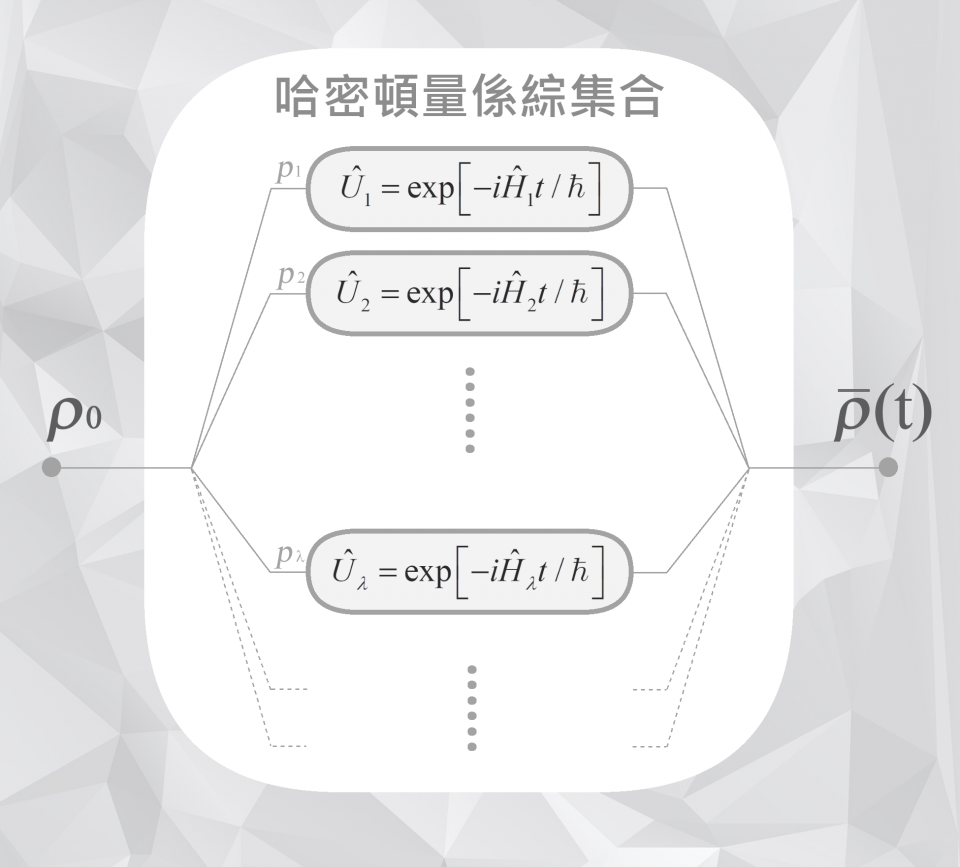
從上面的兩個例子可以得知，想要檢驗一個系統是否具有足夠好的量子性，首先要先提出一個古典策略說明古典的行為應遵守的規範，當發現古典策略不再適用時，就可以確定系統具有某種量子特性。那麼，該怎麼建立規範消相位過程的古典策略呢？這似乎不是一個可以直覺回答的問題。為了建立這樣的古典策略，我們必須先介紹一個重要的工具，哈密頓量係綜集合 (Hamiltonian ensemble, HE)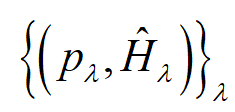 
所謂哈密頓量係綜集合是一個集合，包含了許多的哈密頓量 (Hamiltonian operator)，每個哈密頓量都有各自對應的發生機率 pλ。每當某一個哈密頓量發生後，便可以產生一個相對應的么正時間演化通道 (Unitary time-evolution channel)。我們可以透過圖三來幫助我們理解哈密頓量係綜集合，設想一個黑箱包含了許多的么正時間演化通道，每回合實驗開始後，我們便選擇一個固定的初始態放進黑箱裡，任由黑箱根據機率分布 pλ 將這個初始態指派到某個么正通道。經過多次的實驗後，我們會得到平均末態 
，這個末態便由哈密頓量係綜集合如下決定： 
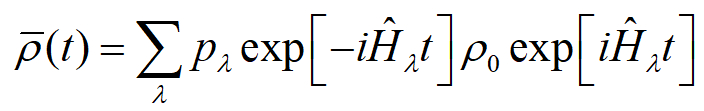
在這種哈密頓量係綜集合所主宰下的平均時間演化，系統會因為哈密頓量係綜集合是統計性混合的原故而逐漸損失其量子同調性。必須特別注意的是，在這種平均時間演化的情況下，其實是沒有一個真實的環境存在的。
系統與環境間的關聯性
現在我們把問題反過來想，當一個真實的量子系統開始與周遭環境交互作用，其量子同調性也會逐漸損失。而我們利用群論嚴格的證明了 [2]，若當系統與環境之間總是保持著一種古典的關聯性，亦即zero discord，那麼這個量子系統的時間演化行為必定正好吻合某一個哈密頓量係綜集合下的平均時間演化。這意味著，考慮一個消相位過程，若我們總是無法以哈密頓量係綜集合模擬這個消相位過程，那麼系統與環境之間必定建立起量子的關聯性，而這個消相位過程就是因為損失了這個未知的量子的關聯性而引起，因此這樣的消相位過程便無法用任何古典的方法加以重現，所以確立了其量子性的本質。
此外，本工作還有額外的一點有趣的地方，這裡特地提出來說明。由上面所述愛麗絲與鮑柏的臆想實驗可知，兩人若要確認手上的量子位元對是否具有量子關聯性，除了各自的測量之外，兩者間相互的通訊以完成量測統計表是不可或缺的步驟。但在本工作中，二體系統可看做是由我們想考慮的量子系統與一個未知的環境所構成，一般來講，這種系統與環境間關聯性是難以確定的，起因於環境大多是難以精準全盤掌握的。但我們現在卻證明了，我們其實只需要系統本身單邊的資訊，就足以進行判斷，這點也是一個相當大的突破。
來自數學激發出的洞見
在了解了哈密頓量係綜集合所主宰下的平均時間演化後，我們再次仔細觀察哈密頓量係綜集合的內容，包含了兩個成分，一個是哈密頓量，另一個是其對應的 (準) 機率分布 ℘λ。接著首先深入探討哈密頓量的部分。因為哈密頓量是厄米特 (Hermitian) 矩陣，所有的厄米特矩陣形成一個su(n)李代數 (Lie algebra)，因此這個部分在數學上已經有充分的研究。另一個成分是 (準) 機率分布 ℘λ，他的隨機變數 λ 正好是哈密頓量的參數，因此可以將這個 (準) 機率分布看作是一個定義在su(n) 李代數參數空間上的一個 (準) 分布函數。每當我們任意給定一個 (準) 分布函數，就可以根據上一節的方法決定一個平均時間演化，這似乎暗示著 (準) 分布函數與開放性系統時間演化之間存在著某種映射 (mapping) 對應方式。因此在物理上，我們的研究重心自然會放在 (準) 分布函數與開放性系統時間演化之間關聯。
定義在局部緊緻群上的傅利葉轉換與頻域空間表示法
從物理的角度來看，一個哈密頓量定義了一個系統所有的能量，故其參數λ自然具有頻率的概念，而哈密頓量係綜集合裡的 (準) 機率分布又是定義在其頻率參數空間上，所以物理上可以想像成是一個開放性系統動力學過程的頻域空間表示法。那麼，我們如何確切的將這種頻域空間表示法的概念表達出來呢？回顧信號分析理論裡，傅立葉轉換是十分重要的工具，因其可將一個時域的信號，轉換成頻域空間分布。因此，要回答上述問題，我們需要廣義化的傅立葉轉換使其可定義在su(n)李代數參數空間。透過數學裡的群表現理論的方法，我們現在可以將哈密頓量係綜集合所主宰的平均時間演化改寫成一個看似傅立葉轉換的方程式，亦即定義在局部緊緻群上的傅利葉轉換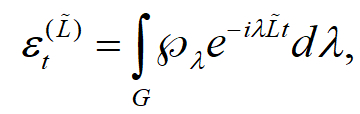 
其中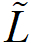
是su(n)李代數產生子 (generator) 的adjoint representation，λ為su(n)李代數參數空間，積分定義在一個局部緊緻群G上，而 
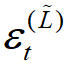則是一個開放性系統時間演化過程在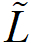基底架構下的矩陣表示法。由於上式是一個類似傅立葉轉換的形式，因此非常充分的展示了℘λ作為一個時間演化過程的頻域分布的角色，也因其是定義在整個su(n)李代數參數空間上，我們便稱其為正則哈密頓量係綜集合表示法 (Canonical Hamiltonian-ensemble representation, CHER) 。至此我們已經完成 (準) 分布函數與開放性系統時間演化之間的映射，換句話說，可用數學上較簡單的 (準) 分布函數來代表一個複雜的開放性系統時間演化過程。而上式在求解的過程將會利用到更多李代數理論裡的概念與定理，本文不在此詳述。
非古典性量化
我們在先前提到，若一個開放性系統時間演化過程無法被以哈密頓量係綜集合模擬，則確立了這個時間演化過程的量子性本質。更精確地說，當我們在求解群上的傅利葉轉換方程式的過程中，若是總免不了得到帶有負值的 (準) 分布函數的解時，這個負值代表了這樣的時間演化過程無法由統計性混和這樣的古典策略達到，因此這個負值是很好的時間演化過程的非古典性指標。那麼我們能否更進一步對這種非古典性加以量化？這個古典性量化的問題便是CHER的一個很好的應用，因為我們現在僅需要使用 (準) 分布函數便可以得到時間演化過程的性質。
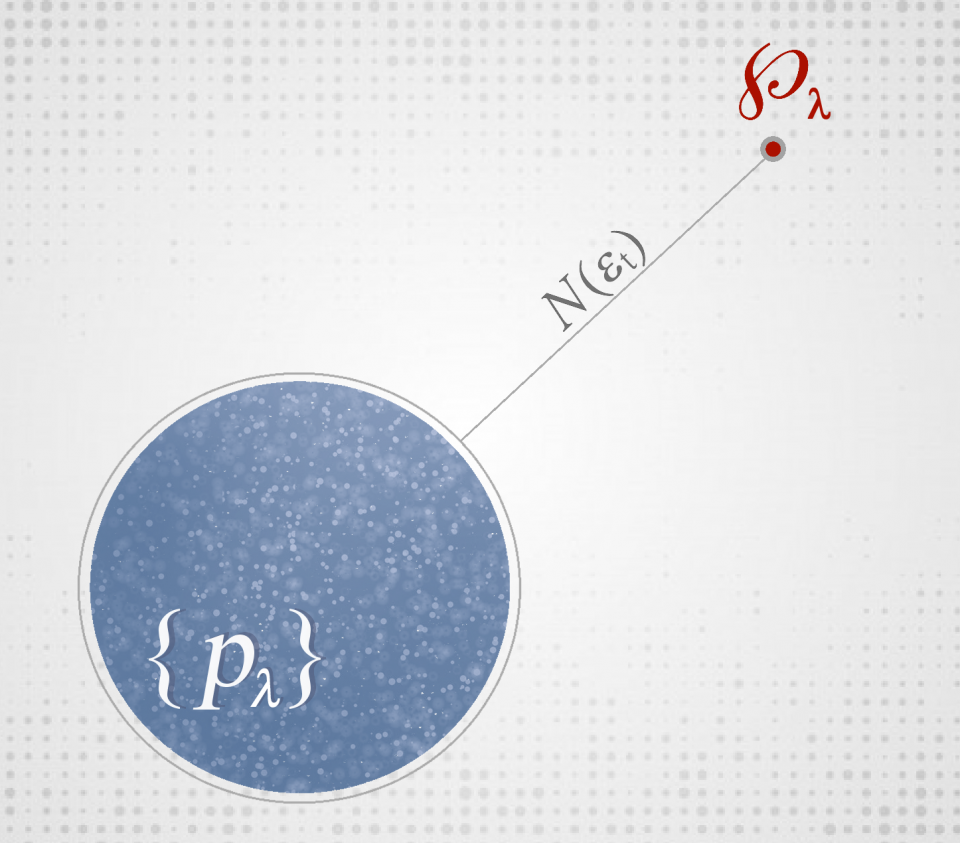
現在考慮所有可能的 (準) 分布函數，他們都是定義在局部緊緻群G上的勒貝格可積函數L1(G)的元素之一。其中所有不含負值的古典機率分布自己形成一個凸子集 (convex subset) 。而在資訊理論裡，常常會考慮到兩個在L1(G)空間裡的 (準) 分布函數之間的”距離”定義如下：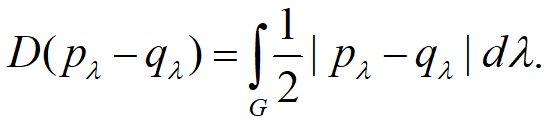 
有了 L1(G)空間裡的距離的概念後，我們就可以問，給定一個開放性系統時間演化過程並求解出其含有負值的準分布函數℘λ，則此準分布函數到古典機率分布所形成的凸子集最短距離有多遠？這個問題可以圖像化地用圖四表示出來。這個最短距離便可以當作是一個很直觀的時間演化過程非古典性測度N(εt)，且從圖四可看出其直觀定義如下：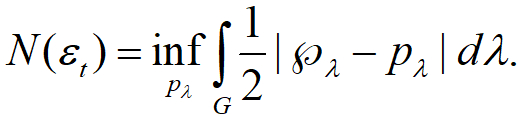 
結語
對於各種量子性質的深入研究與探索，一直是量子物理裡的重要課題，因其幫助我們更加了解這個物質世界運作的基本原理，也每每激發出不同物理分枝發展。這在量子資訊科學裡尤為重要，因高度量子關聯性的系統是不可或缺的資源。在本文中我們探討了，如何透過哈密頓量係綜集合模擬一個開放性量子系統時間演化藉此展現出非古典特性。除了定性上地區分古典性與非古典性外，我們可以更進一步地對一個非古典性的時間演化過程做定量上的測度。藉由李代數理論的幫助，我們可以推導出定義在局部緊緻群上的傅利葉轉換，這因此給予了 (準) 分布函數一個時間演化過程的頻域空間表示法的物理意義。這樣的頻域空間表示法可說是開放性量子系統理論裡非常新穎的概念，未來可望發展出新的研究路線並建立起新的理論研究方法。
參考資料
[1] H.-B. Chen et al., Nature Communications 10, 3794(2019).
[2] H.-B. Chen et al., Physical Review Letters 120, 030403(2018).
[3] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, 2000).
[4] L. E. Ballentine, Rev. Mod. Phys. 42, 358-381(1970).
[5] W. H. Zurek, Rev. Mod. Phys. 75, 715-775(2003).
[6] M. Schlosshauer, Rev. Mod. Phys. 76, 1267-1305(2005).
[7] K. Modi et al., Rev. Mod. Phys. 84, 1655-1707(2012).
[8] E. P. Wigner, Phys. Rev. 40, 749-759(1932).
[9] R. J. Glauber, Phys. Rev. 131, 2766-2788(1963).
[10] E. C. G. Sudarshan, Phys. Rev. Lett. 10, 277-279(1963).
[11] J. S. Bell, Physics 1, 195-200(1964).
隨著各項技術的發展與應用需求的快速成長，尤其是在大數據處理與人工智能等領域崛起的現今，對於高速運算能力的仰賴與日俱增。目前在業界提升運算能力的方法，都是基植於電晶體電路體積的微縮以達到數量與密度上的提升。然而，由於原子的體積自然地定義了一個極限尺度，這種競逐微縮化的過程，終將停止於這個終點線前，無法跨越自然界所設下的這堵高牆。這個問題的根本在於，當元件設計地如此細小時，許多量子的特性便會凸顯出來甚至主導了元件的行為，這使得科學家與工程師們不能再以古典物理的框架來研究設計這樣的元件，否則無法獲得良好的解釋與行為預測。著眼於對未來發展的洞見，元件系統的各種量子特性的深入研究與量化勢在必行。成功大學的研究團隊攜手與來自日本理化學研究所 (RIKEN)、韓國高等技術學院 (KAIST)、交通大學的學者們，共同組成研究群組，探討量子系統的消相位過程與亂序環境影響下的關係，最新研究成果發表於2019年8月22日《Nature Communications》期刊 [1]，且其先導研究也於2018年1月19日發表在《Physical Review Letters》期刊 [2]。
駕馭量子的力量
而在另一方面，若能善用這些奇特的量子特性，也能夠開闢出一條有別於以往的途徑。量子電腦與量子資訊科技就是跳脫了古典物理的框架，建立在量子物理的基礎上而誕生 [3]。量子電腦透過運用量子的特性，達到強大的平行運算能力，可以在極短的時間內完成一般古典電腦難以解決的問題，被認為是下個世代的新興運算工具，並且吸引了全球學界與業界競相投入。而量子電腦之所以擁有強大的運算能力，其關鍵在於量子元件系統可以處於量子疊加態 (Quantum superposition) 以及不同量子元件系統之間可產生量子關聯性如量子糾纏 (Quantum entanglement) 等。在傳統電腦裡，數位化的資料是用二進位運算方式的位元 (Bit) 做為最基本的儲存單位，每個位元的狀態只能處在0或1。而儲存量子資訊最基本的單位則是量子位元 (Quantum bit, qubit)，量子位元可以處於任何 |0〉與 |1〉的疊加態
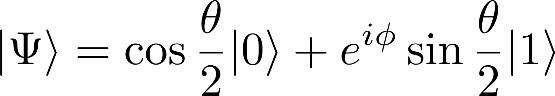
我們也常使用布洛赫球 (Bloch sphere) 這樣的幾何的方式幫助我們圖像化地了解量子態的空間 (見圖一)。因為疊加態的特性，一方面大大擴充了資訊可能儲存的空間，同時也使得量子平行運算成為可能。此外多個量子位元之間所建立起的量子關聯性也是非常重要的量子運算資源，透過不同的手法來操作量子關聯性，可以使得量子資訊能在各個量子位元之間傳遞，甚至可以做到高效的量子遠距傳輸 (Quantum teleportation)，或是隔空操縱 (Quantum steering) 遠方的量子位元，這都是以往的古典電腦所辦不到的。
圖一、用布洛赫球表示法將狀態向量圖像化地表示出來。
技術瓶頸
儘管擁有種種強大的能力與發展願景，量子電腦至今多半還是只侷限於在實驗室內運作，距離商用化還有一段路要走。其中一個最大的技術瓶頸在於，這些特殊的量子特性十分脆弱，很容易因為周圍原子環境的破壞而消逝殆盡。例如半導體量子點中，困陷於位能阱中的電子必須承載在由原子構成的晶格結構，因此無可避免的會與周圍的原子交互作用，尤其是其自旋對於周遭原子核自旋產生的磁場漲落就相當敏感，當電子自旋態製備在某個量子疊加態後，基底之間的相位差會因為周遭的磁場漲落導致其時間演化逐漸變得模糊不確定，最後完全衰退消失，這個過程稱之為消相位。如圖二所示為一對電子形成單態-三態量子位元 (S-T0 qubit) 後，與原子核產生超精細交互作用因而發生不同頻率的消相位過程。量子位元一旦歷經了消相位過程，便失去了量子疊加態的特性，行為將會變的與古典電腦的統計特性一致，因此消相位過程被認為是量子到古典過渡的一個主因 [4-7]。同樣的，這個消相位過程也會破壞多個量子位元之間的量子關聯性，使得量子電腦不再具有量子的特性，因而無法發揮應有的效能甚至頻頻出錯，這樣一來運算效能便大打折扣。因此，深入探討這些消相位機制以及檢測量子性質是否還能持續保有，在提昇量子電腦的效能上是至關重要的課題。猶如現代電子產品在生產的過程中，為確保其產品品質，需要一些品質檢測的程序。
圖二、用布洛赫球來表示單態-三態量子位元消相位過程。
量子性的檢測
那麼，該如何檢測一個量子元件是否還保有量子特性？由於量子元件都相當的微小，任何的直接觀測都會影響到元件的量子態而導致量子態塌縮的發生，如此一來該量子元件就被損毀而不再處於起初欲檢驗的狀態了。因此在量子資訊理論裡，常會使用古典策略模擬的方法。我們首先來看兩個最典型的例子。
第一個例子是光子場量子性的檢測，當給定了一個光子場以及其密度矩陣 ρ 之後我們會透過一些轉換方程將其轉換成Wigner function [8]
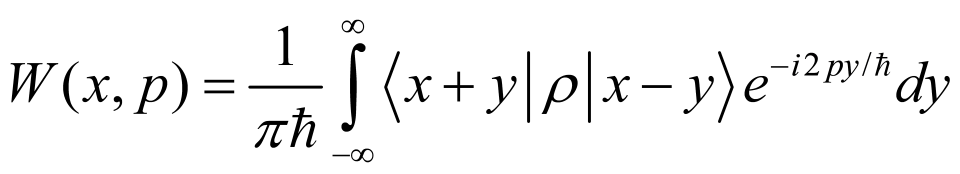
或是Glauber-Sudarshan P representation [9, 10]
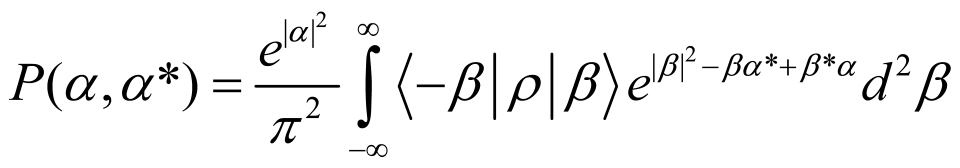
其背後的原理源自於古典物理的相空間表示法。在古典物理中，一個物體的位置及動量可同時被測定，因此以位置及動量做為坐標軸構成所謂的相空間，古典物理便使用分布在相空間中的機率分布來描述物體的行為。借用這樣的概念，Wigner function就是將一個光子場的量子態轉換到相空間，得到相空間中的準機率分布函數。有時候我們會遇到Wigner function出現負值機率甚至奇異點的情況，這些古典物理中不會出現的行為，便是光子場 ρ 的量子特性的展示，因其所包含的負值機率的行為，不能再用古典的方式去考慮。G-S P representation也是類似的概念，只是改成以同調態 (coherent state)
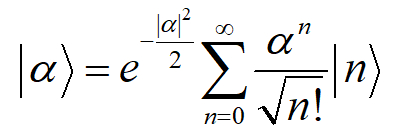
第二個例子是二體量子關聯性的檢測，這在量子資訊理論裡尤其重要，常用一個臆想實驗來說明。假設愛麗絲與鮑柏兩人分隔兩地進行實驗，每回合實驗開始後，他們就會共享一對量子位元，但他們僅能操作他們自己手上的量子位元或者以電話互相通知對方操作的結果 (LOCC)。實驗的目的是要確認愛麗絲與鮑柏所共享的量子位元對之間是否存在著量子關聯性。實驗的進行方式是，每當兩人收到各自的量子位元後，他們便各自選擇某個方向的基底進行測量，接著與對方電話通訊，紀錄彼此的量測方向和量測結果。在重複進行多回合這樣的實驗後，他們就可以完成一份量測的統計表。若這份統計表可以用一組局域隱變數模型 (Local hidden variable model)
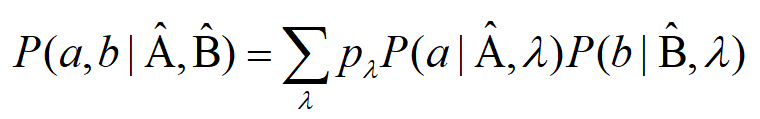
哈密頓量係綜集合
從上面的兩個例子可以得知，想要檢驗一個系統是否具有足夠好的量子性，首先要先提出一個古典策略說明古典的行為應遵守的規範，當發現古典策略不再適用時，就可以確定系統具有某種量子特性。那麼，該怎麼建立規範消相位過程的古典策略呢？這似乎不是一個可以直覺回答的問題。為了建立這樣的古典策略，我們必須先介紹一個重要的工具，哈密頓量係綜集合 (Hamiltonian ensemble, HE)
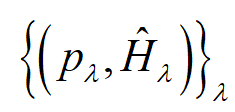
，這個末態便由哈密頓量係綜集合如下決定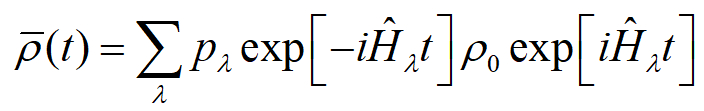： 圖三、哈密頓量係綜集合所主宰的平均時間演化示意圖。
在這種哈密頓量係綜集合所主宰下的平均時間演化，系統會因為哈密頓量係綜集合是統計性混合的原故而逐漸損失其量子同調性。必須特別注意的是，在這種平均時間演化的情況下，其實是沒有一個真實的環境存在的。
系統與環境間的關聯性
現在我們把問題反過來想，當一個真實的量子系統開始與周遭環境交互作用，其量子同調性也會逐漸損失。而我們利用群論嚴格的證明了 [2]，若當系統與環境之間總是保持著一種古典的關聯性，亦即zero discord，那麼這個量子系統的時間演化行為必定正好吻合某一個哈密頓量係綜集合下的平均時間演化。這意味著，考慮一個消相位過程，若我們總是無法以哈密頓量係綜集合模擬這個消相位過程，那麼系統與環境之間必定建立起量子的關聯性，而這個消相位過程就是因為損失了這個未知的量子的關聯性而引起，因此這樣的消相位過程便無法用任何古典的方法加以重現，所以確立了其量子性的本質。
此外，本工作還有額外的一點有趣的地方，這裡特地提出來說明。由上面所述愛麗絲與鮑柏的臆想實驗可知，兩人若要確認手上的量子位元對是否具有量子關聯性，除了各自的測量之外，兩者間相互的通訊以完成量測統計表是不可或缺的步驟。但在本工作中，二體系統可看做是由我們想考慮的量子系統與一個未知的環境所構成，一般來講，這種系統與環境間關聯性是難以確定的，起因於環境大多是難以精準全盤掌握的。但我們現在卻證明了，我們其實只需要系統本身單邊的資訊，就足以進行判斷，這點也是一個相當大的突破。
來自數學激發出的洞見
在了解了哈密頓量係綜集合所主宰下的平均時間演化後，我們再次仔細觀察哈密頓量係綜集合的內容，包含了兩個成分，一個是哈密頓量，另一個是其對應的 (準) 機率分布 ℘λ。接著首先深入探討哈密頓量的部分。因為哈密頓量是厄米特 (Hermitian) 矩陣，所有的厄米特矩陣形成一個su(n)李代數 (Lie algebra)，因此這個部分在數學上已經有充分的研究。另一個成分是 (準) 機率分布 ℘λ，他的隨機變數 λ 正好是哈密頓量的參數，因此可以將這個 (準) 機率分布看作是一個定義在su(n) 李代數參數空間上的一個 (準) 分布函數。每當我們任意給定一個 (準) 分布函數，就可以根據上一節的方法決定一個平均時間演化，這似乎暗示著 (準) 分布函數與開放性系統時間演化之間存在著某種映射 (mapping) 對應方式。因此在物理上，我們的研究重心自然會放在 (準) 分布函數與開放性系統時間演化之間關聯。
定義在局部緊緻群上的傅利葉轉換與頻域空間表示法
從物理的角度來看，一個哈密頓量定義了一個系統所有的能量，故其參數λ自然具有頻率的概念，而哈密頓量係綜集合裡的 (準) 機率分布又是定義在其頻率參數空間上，所以物理上可以想像成是一個開放性系統動力學過程的頻域空間表示法。那麼，我們如何確切的將這種頻域空間表示法的概念表達出來呢？回顧信號分析理論裡，傅立葉轉換是十分重要的工具，因其可將一個時域的信號，轉換成頻域空間分布。因此，要回答上述問題，我們需要廣義化的傅立葉轉換使其可定義在su(n)李代數參數空間。透過數學裡的群表現理論的方法，我們現在可以將哈密頓量係綜集合所主宰的平均時間演化改寫成一個看似傅立葉轉換的方程式，亦即定義在局部緊緻群上的傅利葉轉換
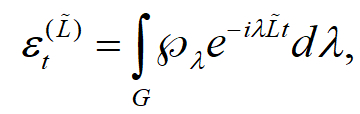
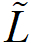是su(n)李代數產生子 (generator) 的adjoint representation，λ為su(n)李代數參數空間，積分定義在一個局部緊緻群G上，而 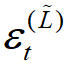則是一個開放性系統時間演化過程在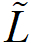基底架構下的矩陣表示法。由於上式是一個類似傅立葉轉換的形式，因此非常充分的展示了℘λ作為一個時間演化過程的頻域分布的角色，也因其是定義在整個su(n)李代數參數空間上，我們便稱其為正則哈密頓量係綜集合表示法 (Canonical Hamiltonian-ensemble representation, CHER) 。至此我們已經完成 (準) 分布函數與開放性系統時間演化之間的映射，換句話說，可用數學上較簡單的 (準) 分布函數來代表一個複雜的開放性系統時間演化過程。而上式在求解的過程將會利用到更多李代數理論裡的概念與定理，本文不在此詳述。非古典性量化
我們在先前提到，若一個開放性系統時間演化過程無法被以哈密頓量係綜集合模擬，則確立了這個時間演化過程的量子性本質。更精確地說，當我們在求解群上的傅利葉轉換方程式的過程中，若是總免不了得到帶有負值的 (準) 分布函數的解時，這個負值代表了這樣的時間演化過程無法由統計性混和這樣的古典策略達到，因此這個負值是很好的時間演化過程的非古典性指標。那麼我們能否更進一步對這種非古典性加以量化？這個古典性量化的問題便是CHER的一個很好的應用，因為我們現在僅需要使用 (準) 分布函數便可以得到時間演化過程的性質。
現在考慮所有可能的 (準) 分布函數，他們都是定義在局部緊緻群G上的勒貝格可積函數L1(G)的元素之一。其中所有不含負值的古典機率分布自己形成一個凸子集 (convex subset) 。而在資訊理論裡，常常會考慮到兩個在L1(G)空間裡的 (準) 分布函數之間的”距離”定義如下：
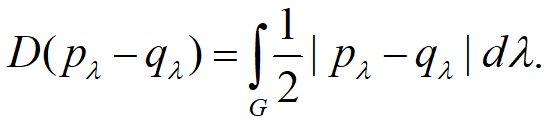
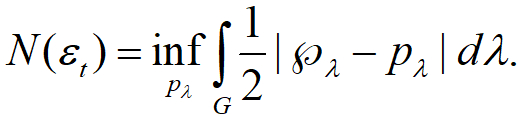
圖四、時間演化過程非古典性測度可直觀地定義為準分布函數到古典機率分布形成的凸子集最短距離。
結語
對於各種量子性質的深入研究與探索，一直是量子物理裡的重要課題，因其幫助我們更加了解這個物質世界運作的基本原理，也每每激發出不同物理分枝發展。這在量子資訊科學裡尤為重要，因高度量子關聯性的系統是不可或缺的資源。在本文中我們探討了，如何透過哈密頓量係綜集合模擬一個開放性量子系統時間演化藉此展現出非古典特性。除了定性上地區分古典性與非古典性外，我們可以更進一步地對一個非古典性的時間演化過程做定量上的測度。藉由李代數理論的幫助，我們可以推導出定義在局部緊緻群上的傅利葉轉換，這因此給予了 (準) 分布函數一個時間演化過程的頻域空間表示法的物理意義。這樣的頻域空間表示法可說是開放性量子系統理論裡非常新穎的概念，未來可望發展出新的研究路線並建立起新的理論研究方法。
參考資料
[1] H.-B. Chen et al., Nature Communications 10, 3794(2019).
[2] H.-B. Chen et al., Physical Review Letters 120, 030403(2018).
[3] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, 2000).
[4] L. E. Ballentine, Rev. Mod. Phys. 42, 358-381(1970).
[5] W. H. Zurek, Rev. Mod. Phys. 75, 715-775(2003).
[6] M. Schlosshauer, Rev. Mod. Phys. 76, 1267-1305(2005).
[7] K. Modi et al., Rev. Mod. Phys. 84, 1655-1707(2012).
[8] E. P. Wigner, Phys. Rev. 40, 749-759(1932).
[9] R. J. Glauber, Phys. Rev. 131, 2766-2788(1963).
[10] E. C. G. Sudarshan, Phys. Rev. Lett. 10, 277-279(1963).
[11] J. S. Bell, Physics 1, 195-200(1964).