海森堡談理論、批判與哲學(上)

阿卜杜勒·薩拉姆 (Abdus Salam)—「只有王才能服事王」

 

        波斯沙王—納迪爾沙(Nader Shah)於1748年入侵印度，他朝德里步步進逼。在狠狠的重創印度莫卧兒(Mogul)帝國後，德里投降了，於是兩位國王進行了和談。談判的結論包括：將著名的孔雀寶座從德里運往伊朗，戰敗國的大維齊爾(Grand Vizier, 相當於宰相) 阿西夫扎(Asifjah)被召喚來向兩位國王獻酒為和平舉杯。這位大維齊爾陷入了外交禮節上的兩難。他到底該先向誰獻酒呢？若先向自己的主子獻酒，那惱羞成怒的波斯人可能會拔刀斬掉他的腦袋，反之亦然。這位大維齊爾終於想到了一個高明的主意。他將放了兩杯酒的金色托盤呈給他的主人並推辭説，今天實在輪不到我來獻酒，只有王才能服事王。讓我懷著同樣的心情，懇請今天議題的大師，狄拉克(Dirac)教授來介紹另一位大師—維爾納·海森堡(Werner Heisenberg)教授。
 

圖：維爾納·海森堡(Werner Heisenberg) 圖片來源：wikimedia common

 

保羅·埃德里安·莫里斯·狄拉克(P.A.M. Dirac)—「一個黃金年代的開啟」

 

        我有最好的理由成為維爾納·海森堡的景仰者。當年他和我都是年輕的研究生，我們年齡相當，做著同樣的問題；但在我失敗的地方海森堡卻成功了。當時累積了大量的光譜學數據，而海森堡找到了處理它們的正確方式，他因此開啟了理論物理的黃金年代。使得在此後數年內任何一個二流的學生都可以輕易完成一流的工作。
 

        在那之後，我有幸可以和他一起旅行。在日本，我發現他對登山十分在行且具備絕佳的平衡感。我們需要爬一座有平頂的塔，旁邊有石欄杆環繞著。在石欄杆的四個角落稍有隆起。海森堡爬上欄杆後再爬到角落的隆起處，他可以完全沒有依靠的站在上面，就這樣立足於大約六平方英吋大小的石塊上。他只顧著飽覽四周的美景，絲毫不畏懼其身處之高處。我不禁為他揑了把冷汗，萬一來了一陣風後果可就不堪設想了。



維爾納·卡爾·海森堡（Werner Karl Heisenberg）—進入物理的第一步
 

        我由衷的感謝狄拉克的介紹。我想要就我的記憶，來回顧早年人們如何從事理論物理的研究。人們持着許多不同的態度：有人嘗試建構現象學的理論，有人思索著嚴謹的數學架構，也有人思考著相關的哲學；我想要逐個檢視這些方法並與我自身從事物理的經驗相聯繫。

  
  就在我進入大學後不久，當時的慕尼黑大學理論物理學教授索末斐（Sommerfeld）有一天來找我說：「既然你對原子物理感興趣，那你要不要來試試看解一個問題呢？」當時我對他的提議感到興致勃勃、躍躍欲試，只是我對物理所知尚淺；但他告訴我說，這相當容易，它大致上就像在玩填字遊戲而非做嚴謹的數學。

 

索末斐教授提出問題是這樣的，他剛收到有關反常季曼效應（anomalous Zeeman effect）_[2] 的光譜線相片，我（海森堡）想它們是杜賓根（Tübingen）的物理學家巴克（Back）所拍攝的，索末斐對我説:「來，已知有這些譜線，現在你試試看，根據波耳（Bohr）的理論來計算或決定這些譜缐所對應的能階，使得每一條譜線可由兩個能階的差來表示，再指定其(能階的)量子數，然後你就應該可以回過頭來重建出那些譜線了。」

 

        理所當然的我們要嘗試將能量表示成量子數或其他類似東西的函數。我初次的嘗試以一場災難結尾，因我發現必須引入二分之一丶二分之三等半整數的量子數，索末斐對之十分震驚。他認為這結果全都是錯的， 而我的朋友兼同學沃夫岡·包立(Wolfgang Pauli)對我說，「倘若你引入半整數的量子數，不久之後你將引入四分之一的整數，然後是十分之一的整數，到後來你勢必回到連續的量子數，到時我們又再次回到古典物理理論了。」過了一陣子，我們當中有更多的人對這些問題感興趣了，其中包括包立、洪納（Hönl）和其他人。後來我們發現，還真的需要引入半整數的量子數。當時我們有一羣不錯的年青人一起做現象學方面的研究，發明著能重現實驗結果的式子；朗德（Landé）的公式、索末菲和洪納的多重態（multiplet）公式和其他的式子就是這樣被一一的發現。

 

現象學理論
 

        在這些嘗試中有一件事令我最為印象深刻，我想我應該談談它，也好説明現象學理論的極限。索末斐告訴我一篇在哥廷根的佛依格特（Voigt）在1913年所寫的老文章，比波耳的原子理論更早。佛依格特給出了一個有關鈉D譜線季曼效應的理論。他引入了兩個互相耦合的振子，它們被仔細安排好以給出那兩條D譜線，而他也可以通過調整其耦合常數來得出反常季曼效應，甚至可以得出帕申—巴克效應(Paschen-Back effect)和正確的光譜強度，整體來說佛依格特可以很好的重現實驗結果。索末菲叫我以量子論的語言重新翻譯這些結果，我發現這可以輕易達成。我找到了一些關於能階和譜線強度相當複雜的冗長公式，這些式子有長的開根號，其中包含了磁場的開根號、耦合常數等，而實驗結果也可以很好地被量子論重現。我談到這麼一個現象學的陳述，因它可以與實驗結果非常吻合，但它到底與量子論有什麼關係呢？六年以後我們有了量子力學 ，喬登(Jordan)和我嘗試用量子力學來計算這些譜線和強度，我們得出了和佛依格特完全一模一樣的式子，一様的長根號和一様的強度。所以一方面你看到，現象學理論可以非常的成功，有時它們甚至可以給出正確完全吻合於實驗的結果，但同時它們卻沒有提供任何與該現象物理內涵有關的真實資訊—也就是那些在原子中真正發生的事情。當然，我們現在終於可以釐清這其中的原因：

"    在量子力學反常季曼效應的計算中，人們需要去解一個以特徵行列式(secular determinant)表示的微擾相關問題；該特徵行列式有一組線性方程式，其中有幾個未知數。而兩個互相耦合振子的系統正好具有這樣的數學結構，它也有幾條線性方程式和幾個未知數。我們終於了解到這兩個理論雖然在形式上相同，但其物理內涵卻是截然不同的。   "

      

  這些現象學嘗試真正的成功，是在一個稍微不同的方向上。當時我們經常試著在各種情況下，將我們從實驗獲得的公式和波耳的理論相比較；一些非常有趣的事發生了。雖然我們發現不可能完全用波耳的理論得出這些公式，但我們仍可以從波耳的理論得到一些與真實公式相近的式子。例如，在波耳理論中我們預期會出現角動量平方(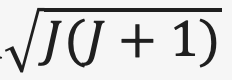J²)的地方，在經驗式上卻出現了J(J+1) 這樣的東西。今天這樣的結果是相當然顯而易見的，因為這只不過是群表徴（representations of groups）罷了。但在當時這是一個非常奇怪的結果，它似乎表示波耳理論是正確的，但它好像又有些不太對勁，我們對它還真是不知所措。因為至終所有的量子數，以角動量為例，是不可能從古典物理跑出像這樣的東西的。我們對此感到相當的沮喪，但同時我們對波耳當時的一些文章極度感興趣。當時波耳才剛發表了幾篇與元素週期表有關的文章。我們知道這些元素的原子具有非常複雜的結構，它們有十個、二十個或三十個電子在不同的軌道上，我們不知道波耳到底如何獲得那些結果。我們覺得他一定是一位超級絕頂聰明的數學家，竟然能解決這些如同古典天文學中令人望而生畏的(多體)問題。我們知道就是最好的天文學家，對三體問題也都是一籌莫展的，而現在波耳竟然可以解決這些具三十來個電子的問題。

 

波耳的猜想
 

        經過了兩年的學習後，在 1922年夏天，索末斐問我是否願意隨他出席一個在哥廷根的會議，波耳將會報告其理論。我們現在都把那段在哥廷根的日子稱為「波耳節慶」(Bohr-festival)。直到那時我才知道像波耳這様的人是如何從事原子物理的研究。上了波耳的兩次課後，我大膽的在一次的討論中提出了一些評論；我質疑他在黑板上寫下克拉莫（Kramers）公式的正確性。從我們在慕尼黑的討論得知，所獲得的公式常是半精確半對半錯的，所以我以為我們是不能太肯定的。波耳非常友善，我雖然只是一個年輕的學生，他還是邀請我一起到哥廷根附近的海因貝格（Hainberg）散步討論問題。在此之後，我才真正懂得在一個嶄新的領域做理論物理研究到底是怎麼一回事。對我而言，相當震撼的初體驗是波耳並沒有做任何的計算！他只是猜出他的結果。他知道化學的實驗結果，他知道各種原子的原子價，並且他知道他那軌道量子化的想法（以量子化來解釋原子的穩定性的想法）和化學的實驗結果大致是相吻合的。他就是這樣單單猜出那些所呈現的結果。我問他，是否真的相信，人們可以用古典力學來推導出這些結果。他說：「這様說吧！我想這些古典的圖象，就是我所描繪的原子圖象，它們的可靠程度和古典圖象本身的可靠程度是一樣的。」他接著解釋說：「我們現在是在物理的一個新領域，我們知道舊的觀念大概不適用了。我們發現它們不適用，否則原子就不能穩定了。但在另一方面，當我們要談到原子時，我們必須使用來自舊觀念、舊語言的字句；所以我們正處於一個令人絶望的兩難之間。我們好比一些來到一個非常遙遠國度的水手們，我們不知道那個國家，我們看見當地居民，其語言是我們未曾聽聞的，我們不知道要如何溝通。所以，在古典圖象仍然適用的範圍內，就是如果我們仍然可以談論有關電子的運動，有關電子的速度，有關電子的能量等等時，我想我的圖像是正確的或説起碼我希望它們是正確的，但是沒有人真正知這語言的適用範圍。」

        這對我而言是一個非常新穎的想法，它徹底的改變了我對物理的整個看法。在索末裴的學派中，理所當然的是，你必須計算一些東西，而只有通過嚴謹的計算你才能獲得好的結果。

 

矩陣力學的誔生_[3]
 

        現在回到現象學理論的探討。與波耳的討論讓我獲得以下的印象：我們應該要全然摒棄這些相關的古典觀念，我們不應該談論電子的軌道。雖然你可以在雲霧室中觀察到電子軌跡，但你不應該談論其速度或位置等這些東西，然而你若摒棄這些字句，則你將不知道該怎麼辦了。所以這是一個十分奇特的兩難困境，而一個極有趣的問題是，「在此處境之下，我們可以做什麼？」
 

         與波耳談話不久後(我想應該是半年後)，我到哥本哈根去，和克拉莫一起研究色散(dispersion)理論。我們再一次發現這個有趣的情況，從波耳理論推導出來的公式似乎是對的，但它們又不是完全正確。我們慢慢發展出一種處理這類公式的習慣，可以將古典物理的結果翻譯成這些現象學的公式。我們已經體會到，至終勢必有某種量子力學來取代古典力學，而它和古典力學的差異似乎沒那麼大，但它必定使用十分不同的觀念。
 

        人們常說在這個情況下，我們與一個單單使用可觀測物理量的正確理論只有一步之遙了。事實上這様的聯繋是十分自然的，因為我們知道可以使用頻率和振幅；而它們在古典理論中可以用來取代電子的軌跡。一整套的頻率和振幅代表一個傅立葉級數，而一個傅立葉級數描述一個軌跡。所以很自然的人們應該使用成套的頻率和振幅而非軌跡。
 

        當我從哥本哈根回到哥廷根後，我決定我應該也要試試看做一些猜測，我要猜猜氫原子光譜的強度。波耳理論不能處理這些強度，但為什麼不去猜猜它們呢？當時是1925年的夏天，我的嘗試徹底的失敗了。這些公式變得越來越複雜，以致於不太可能從中獲得仼何東西。在此同時我覺得，倘若處理的力學系統比較簡單一些，則似乎有可能只要使用我與克拉莫在哥本哈根猜測振幅一様的那套做法就行了。就這様我轉而研究非簡諧振子，它是一個很簡單的模型。然而就在這個時候我卻病倒了，我去到黑爾戈蘭島(Heligoland)養病，在那裡我有充裕的時間來做計算。我發現可以輕易地將該模型的古典力學結果翻譯成量子力學結果。但我要強調一個重點：單單啟用「讓我們以頻率和振幅取代軌跡」及使用我們在哥本哈根的那一套做法(它後來被証明和矩陣乘法等價)是不夠的。
 

        顯然的，倘若人們只是如此做，所得的理論架構遠比古典理論更為開放。古典理論當然可以被納入其中，量子理論也可以被納入，但此架構卻過於含糊，以致於我們需要加入其他額外的條件來限制它。

        後來我發現，可以將波耳理論的量子化條件，換成托馬斯(Thomas)和庫恩(Kuhn) 求和法則的等價式子。[4] 加入該式後，突然之間我得到了一個自洽的架構。這套假設奏效，它可以獲得能量是常數等等正確的結果。然而我卻無法找出一個簡潔的數學架構。不久後哥廷根的波恩(Born)和喬登，以及劍橋的狄拉克發明了一個完美封閉的數學架構；狄拉克用了精彩絕倫的q數，而波恩和喬登則採用較為傳統的矩陣方法。

 

愛因斯坦論理論與觀測
 

        與其進一步談論上述發展的細節，現在我倒想談談 「該發展中最核心部分的哲學」這個議題。剛開始時，我以爲這可能就是指，只引入可觀測量的觀念；但當我於1926年在柏林講論量子力學時，愛因斯坦聽了我的演講後，糾正了上述看法。
 

        在我的演講之後，愛因斯坦邀請我到他的公寓討論。他劈頭就問: 「你那個非常怪異的理論背後的哲學是什麼? 那個理論看起來不錯，但你提到只討論可觀測的物理量卻是什麼意思呢? 」我回答說，雖然電子在雲霧室可留下軌跡，但我再也不相信電子軌道這碼事了。我覺得我們應該回歸到那些能真正被觀測到的物理量，同時我也覺得這正是他在相對論中所採取的哲學，因為他也放棄了絶對時間，並引入與座標系有關的時間。愛因斯坦不禁笑了起來，並對我説：「但是你應該知道，它是全然錯誤的。」 我回説： 「這是為什麼呢? 你不是用了這樣的哲學嗎? 」他説：「沒錯，我是用過它，但它仍然是一派胡言! 」
 

        愛因斯坦向我解釋，事實上事情正好倒過來。他説：「你是否能觀測某個東西，取決於你所用的理論。理論才真正決定了什麼是可以被觀測的。」他的論點如下： 「觀測指的是，我們在現象及我們對該現象的理解間建立起某種聯繫。在原子中發生了一件事，發出光來，光照在相片上，我們看到該相片等等等。對於這整串介於原子到你的眼睛和你的意識之間所發生的事件，你必然假定一切按照古典物理來發生。你如果改變了描述這串事件的理論，則你的觀測也必然改變。」所以他堅決認為，是理論決定了什麼可以被觀測。愛因斯坦的評論，對於日後我與波耳嘗試探討量子力學的詮釋時起了重要的影響。我們以後再回頭來談這件事。
 

        讓我再談談我與愛因斯坦的談話。愛因斯坦指出，只允許談論可觀測的物理量是極危險的。因為所有合理的理論，除了有可以立即觀測的量，也允許比較間接的觀測量。舉例來說，馬赫相信原子的觀念不過是關於點的方便想法，他不相信原子的真實性。現在大家都覺得這是胡扯，人們很清楚原子是真實存在的。我也覺得，從為了方便而提出原子觀念(雖然在邏輯上是有可能的)的作法上，人們是不能獲取任何益處的。這些是愛因斯坦所提出的觀點。對於量子論，這表示有了量子力學，你不只有頻率和振幅，你也有機率振幅、機率波等等，這些當然是很不一樣的東西。
 

       我應該再補足一點。當人們發明一個描述某些觀測量的新架構時，當然其決定性的問題是：你可以丟棄那些舊觀念？在量子論的例子中，可以或多或少的清楚看出，人們可以丟棄電子軌道的觀念。

 

層流的穩定性
 

        現在讓我放下現象學理論的問題，而來問一個相反的問題：「精確的數學架構有什麼用處呢？」也許你們知道我並不特別欣賞嚴謹的數學方法，且讓我為此態度提出幾個理由。這關係到發生在建構量子力學之前那幾年間的事，當時我需要完成我的博士論文。索末斐是個好老師，他覺得我不應該單單從事原子理論的研究；他對我說，「老是在泥巴中行走並不是一件好事，你真的應該在理論物理中，好好的做一點像様的數學工作了。」於是他提出了一個流體力學的題目。要我去計算分析層流(laminar flow)的穩定性。他自己曾發表過一篇有關這個主題的文章，他的一個學生曾經處理過在一個靜止的器壁和一個活動的器壁間的流體的層流問題；索末斐對他的結果並不滿意，這位學生霍普(Hopf)無法找到層流的穩定性極限。實驗上大家都知道當速度加快到一定的程度時，層流會轉變成湍流(turbulent flow)，旋渦會隨機出現，這看起來就像是一個不穏定的現象。所以應該可以計算出，由層流轉變成湍流的層流穩定性極限。索末斐建議我應該去計算在兩片固定器壁間的水流的穩定性。這就是我的博士論文題目，而我相信我也取得了一個不錯的結果，我找到了該流體的穩定性極限。在某個與實驗吻合的雷諾數(Reynolds number)下，該流體變成不穩定的湍流。
 

 

二十年後的續篇
 

        我就這樣以那篇文章取得我的學位，但是在一年以後，一個很優秀的數學家諾特(Fritz Noether)發表了另一篇文章，他以非常嚴謹的數學方法證明，該問題沒有不穩定的解，流體到處都是穏定的。對我來說，這當然是相當悲慘的事了，尤其這關係到我的學位，所以我一直想要推翻諾特的結論。不幸的是我無法反証它，於是我只好寄望於實驗，因為在實驗上確實有穩定性的極限。這個問題經過了好些年才慢慢獲得了澄清，也許我可以談談其中的一些過程。五年以後托爾明(Tollmien)處理了另一種流體，並確實得到穩定性的極限，他可以宣稱他硏究的問題和諾特的不同，故諾特的數學推論派不上用場。再來是1944年，也就是我完成博士論文20年後，在美國的德萊頓(Dryden)和他的合作者，對兩片器壁間的層流及其到湍流的????變做了很精確的測量。他們發現我的計算和實驗的結果互相吻合。在麻省理工學院的林家翹接著研究這個問題，並採用了更新及更好的方法，確認了舊的結論(海森堡的結論)。然而有些數學家還是不予採信，於是我們1950年在麻省理工學院，針對此問題進行了相當冗長的討論，然後馮諾依曼(von Neumann)決定，我們應該試著用電腦來處理看看。於是當時最大的電腦就用來解這個問題，結果我在論文中的近似計算結果和電腦跑出來的結果只有不到20%的誤差。那下一個問題是「那篇嚴謹數學的文章到底怎麼了？」。麻煩的是，我想至今沒有人知道它到底那裡出了問題。

 

發現一個數學的錯誤
 

       在另一個故事裡我們知道錯誤在哪邊。那是愛德華·泰勒(Edward Teller)約於1928年到我在萊比錫的研究所時的事了。他想要做一篇博士論文，我沒有給他有關湍流的題目。因為當時量子力學已經算得上是像樣的物理了，所以我建議他也許可以研究氫分子離子，那是一個由兩個質子和一個電子組成的系統。我告訴他波耳的一個學生，布勞(Burrau)，剛發表了一篇有關此分子離子正常態的好文章。他得到有關束縛能的結果和實驗吻合。泰勒應該去研究其激發態。

        幾個禮拜後，泰勒到我的辦公室來告訢我說，最近威爾森(Wilson)發表了一篇新的文章，他使用很好的數學方法，比布勞的更好更嚴謹，証明氫分子離子的正常態不存在。這又是一個不幸的結果，我告訴泰勒這一定是錯的，因為畢竟此分子離子的確存在，這是人們無法改變的事實。但泰勒説：「威爾森的數學是那麼的好，你不能找出任何可反駁之處。」於是泰勒和我為之爭論不休。我想大約過了兩個月後，泰勒確實找出了威爾森文章的錯誤；這是一個相當有趣的錯誤。威爾森的數學方法確實是很漂亮的，但他推論説，「我們知道薛丁格波函數在離兩個中心很遠處必須趨向零，」這是對的，「所以我們的解析函數必須為正則的，且在無限遠處為零」，這是錯的，因為我們只需要求在(距離的)實數軸上它會趨近於零就足夠了，不必要求在虛數軸上也如此。這是一個人們可能會犯的錯誤，我希望諾特在湍流的研究上也犯了類似的錯誤，但我不知道到底實情是怎樣。

 

嚴謹和骯髒的數學
 

        我想你們現在可以理解我為什麼老是對嚴謹的數學方法不太放心了，也許我應該提供一個比較嚴肅的理由。當你用太多嚴謹的數學時，你把你的注意力放在一些對物理而言不太重要的點上，因而遠離了實驗的處境。反之若你用比較骯髒的數學方法，如同我經常做的，你將被迫專注在實驗的景況上；無論你寫下任何一個式子，你都試著與真實世界作比對，如此一來將比用嚴謹數學更能接近事實的真相。但是當然，這是因人而異的。

---

本文翻譯自A. Salam, H. A. Bethe, P. A. M. Dirac, W. Heisenberg, E. P. Wigner, O Klein, E. M. Lifshitz, From a Life of Physics, World Scientific Publishing Co. Pte. Ltd., Singapore, 1989, pp. 31-44 (Werner Heisenberg, Theory, Criticism and a Philosophy), http://www.worldscientific.com/worldscibooks/10.1142/0877, 感謝世界科技出版有限公司授權翻譯。

---