粒子物理行（六） 四種基本力-----重力交互作用

重力交互作用即是萬有引力。重力交互作用的交互作用荷是能量和動量。由於能量和動量是一切物質都擁有的物理量，重力交互作用發生在所有物質身上。任何兩件物體都會互相作用一重力吸引力。可是，這種吸引力的強度非常弱。例如，兩顆電子之間的靜電排斥力比它們之間的重力吸引力大10⁴¹倍。在微觀世界裏，重力小得可以被完全忽略。但是，由於電荷可正可負，而正負電荷傾向互相吸引組成電荷中性的物質 (例如帶負電荷的電子和帶正電荷的質子互相吸引，組成電荷中性的原子)，宏觀物體的總電荷非常小，所以兩不相碰的宏觀物體之間的靜電力非常小。重力的交互作用荷是能量和動量。在速度遠低於光速的情況下，物體的動量遠小於能量，並且能量與質量的值很接近【註1】。由於物質的質量只能取正值，重力的交互作用荷都是加起來越來越大，並沒有像電荷的正負抵消現象。

“  所以，只要兩宏觀物體的質量足夠大，它們之間的萬有引力遠大於静電力。這就是為什麼天體運動都由重力主宰，如月球環繞地球運動、地球環繞太陽運動、太陽系環繞銀河系中心運動等。“

 

廣義相對論

描述重力的經典理論是廣義相對論。廣義相對論把時空視為一幾何個體，時空曲率的一部份正比於物質的能量和動量【註2】。在只有重力的在作用下，粒子在時空的軌跡是彎曲時空中的短程線。曲率和短程綫的概念可以用平面和球面來簡單理解。

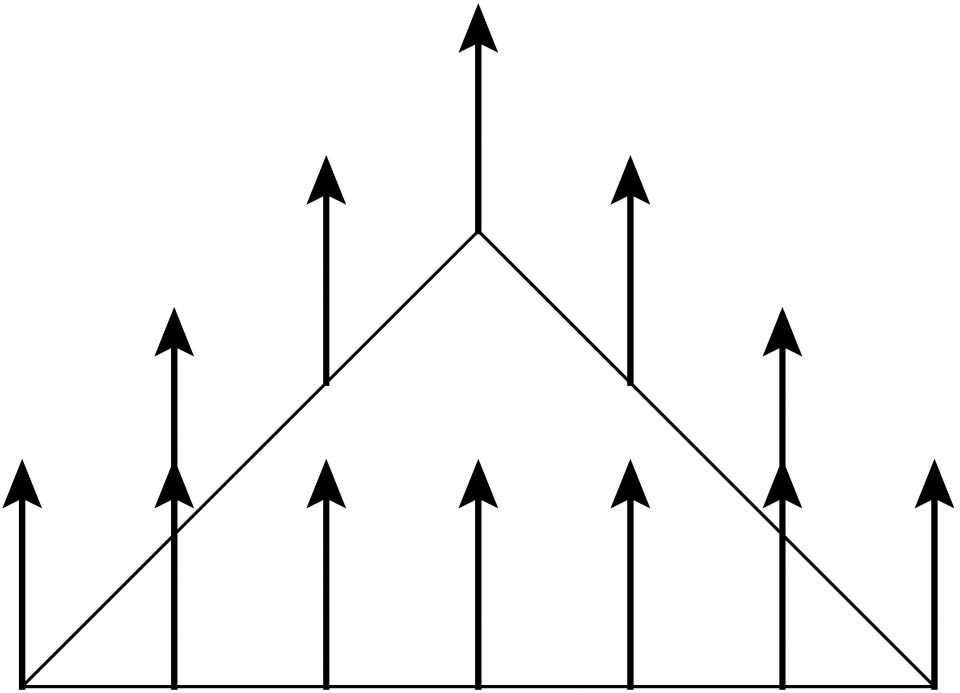
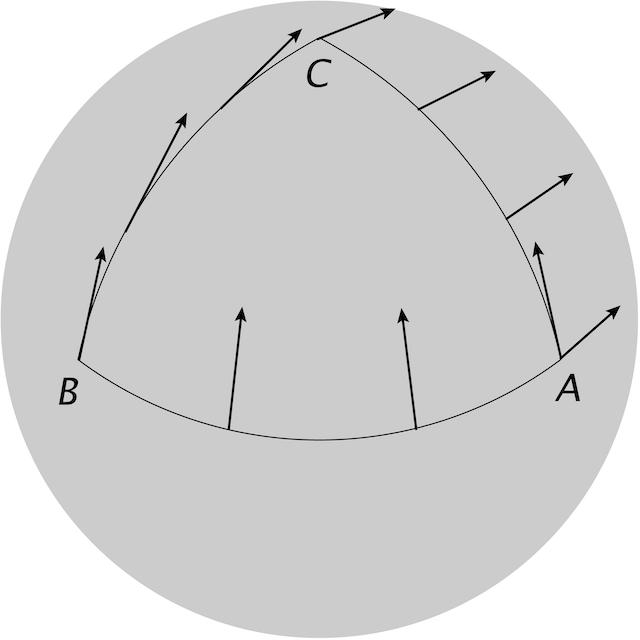
假設我們站在一無限大的平面上，我們有什麼辦法判斷該面是平的還是曲的？假設我們拿着一枝平行於地面的箭在地面上行走，並且在每一時刻保証箭頭方向不變。我們稱這樣把箭頭運輸為平行運輸 (parallel transport)。這裏，「平行」指方向局部不變。假設我們帶着箭頭平行運輸在平面上走了一圈返回原位 (見圖一)。如圖所示，箭頭的最終方向與初始方向相同。這是空間曲率為零的表現。考慮如圖二中球面上的閉合曲線，它是球面上的三角形，每條邊都是四分之一個大圓【註3】，每個內角都是90度。箭頭被沿着此三角形平行運輸，結果箭頭的最終方向與初始方向並不相同，差了90度！這顯示了球面具有非零曲率。

 

圖一

圖二

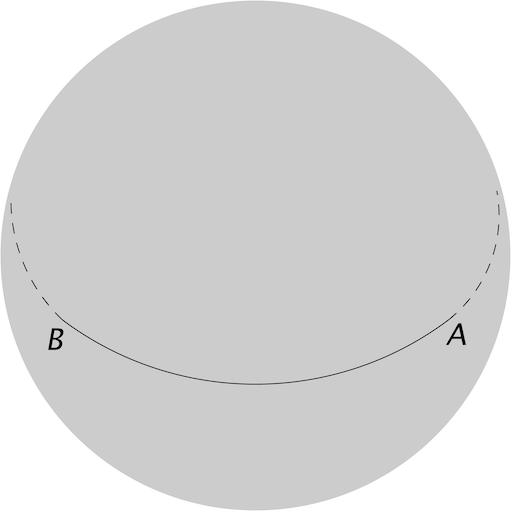
短程線是彎曲空間中的直線。短程線被定義為局部不轉彎的曲線，即切向量被平行運輸的曲線。圖二中球面上三角形的三條邊便是短程線。「短程線」這名稱有點誤導，因為有些情況下短程線並非連接給定兩點的最短路線。圖三顯示了圖二中的A點和B點，實線和虚線都是連接A點和B點的短程線。實線是四分之一個大圓，而虚線是四分之三個大圓。實綫是連接A點和B點的最短路線，但虛線並不是，雖然它也是短程線。

圖三

從廣義相對論的觀點看，地球之所以環繞太陽運動，是因為太陽巨大的質量對應巨大的能量，因此時空被扭曲，而地球在彎曲了的時空中沿短程線運動。在有重力以外的交互作用下，例如電磁交互作用下，粒子的運動並不沿時空短程線，而運動與時空短程綫的偏離由重力以外的交互作用力給出。例如一隻杯站在桌上 (圖四)，杯底和桌面原子之間的電磁交互作用使杯不遵從時空短程線 (自由掉落) 運動，而是保持靜止的站在桌上。值得注意的是，F_g是整個地球作用在整個杯上的重力，而F_N (如上一章所述) 只不過是與杯底接觸的桌面原子作用在杯底原子的靜電斥力。可是，F_g和F_N大小相同，互相抵消，導致杯的加速度為零。從這個例子，我們可見粒子間的電磁交互作用遠遠大於重力交互作用。

 

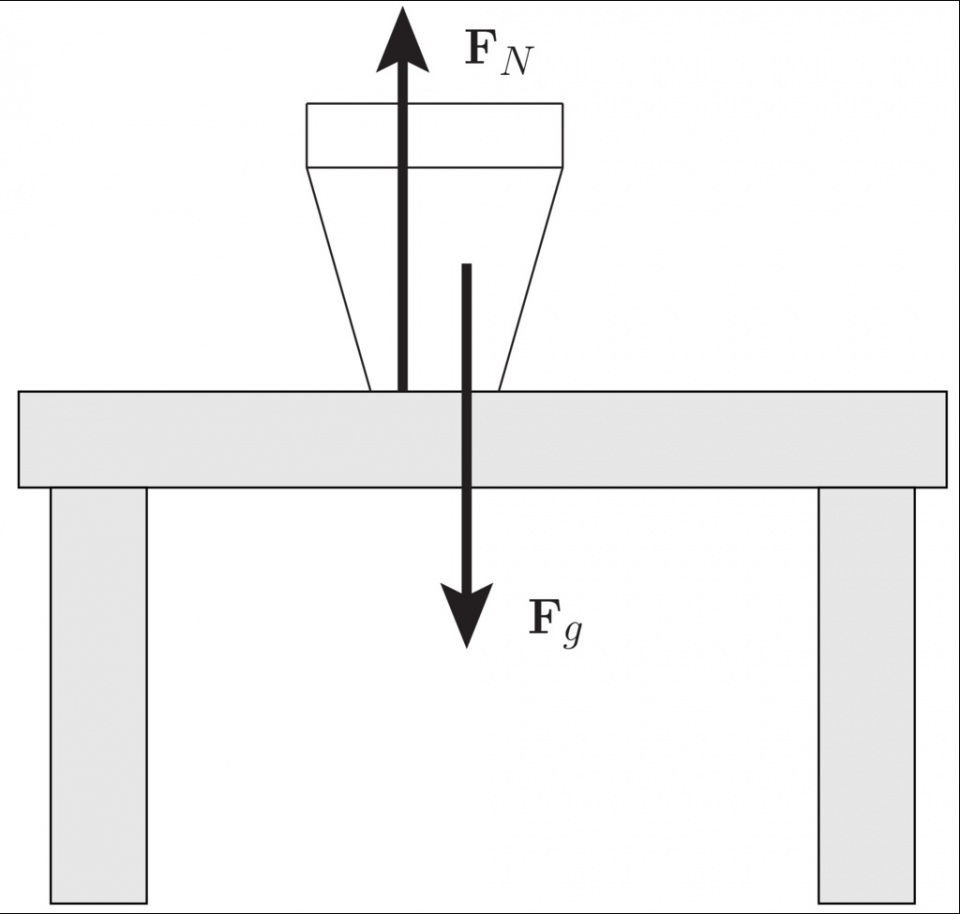
圖四

當物體的速度接近光速時，動量的大小與能量相當，是不可被忽略的重力交互作用荷。例如光子在經過太陽時運動方向會因太陽所產生的重力場而改變 (見圖五)，而改變的角度一半來自光子的能量，一半來自光子的動量【註4】。因為牛頓重力理論並沒有把動量對重力的貢獻考慮在內，廣義相對論預言的光的偏轉角度是牛頓重力理論預言的兩倍。英國天文學家愛丁頓 (Eddington) 在1919年的日全蝕中觀察到位於太陽後面的恆星發出的光，證明了太陽的重力場的確改變了鄰近光子的運動方向，並且光的偏轉角度與廣義相對論的預測吻合【註5】。



 

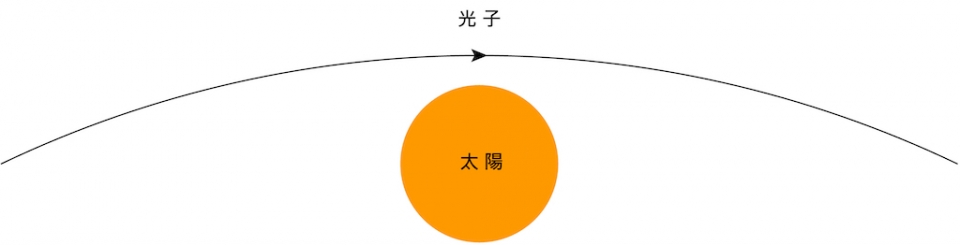
圖五

給定一個質量為m的物體，我們可以簡單判斷距離物體中心r的位置處時空的彎曲程度大小。考慮參數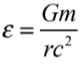，其中G是牛頓重力常數，c是光速。如果ε ≪1，那麼時空彎曲程度很小，牛頓重力理論適用【註6】,如果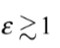時空彎曲程度很大,必須使用，時空彎曲程度很大，必須使用廣義相對論。對於地球表面，我們可代入地球的質量和半徑，得到ε ~ 10⁻⁹。所以，在地球附近的範圍，牛頓重力理論適用。可是，對於極精準的理論預測，我們還是要倚賴廣義相對論。根據廣義相對論，重力場愈強，時間走得愈慢。例如，如果遥遠的外太空過了時間Δt，地球表面上則過了時間(1− ε )Δt。全球衛星定位系統 (GPS) 依照接收人造衛星以無線電波形式放出的時間數據來判斷訊號接收者的位置。由於光速很大 (每秒30萬公里)，人造衛星上的時間量度必須十分精準，甚至須要把地球表面和太空中時間的極微小差異考慮在內。所以，每當我們使用手機的GPS功能，我們都在應用廣義相對論！

 

宇宙中的質量分佈在大尺度下是均勻的【註7】。所以，在大尺度下，半徑r 的球體範圍內包含的質量正比於r ³，因此 ε 正比於 r²。也就是說，只要 r 足夠大，ε 便會大於1。因此，在考慮整個宇宙的演化時,我們必須使用廣義相對論【註 8】。

慣性的本質

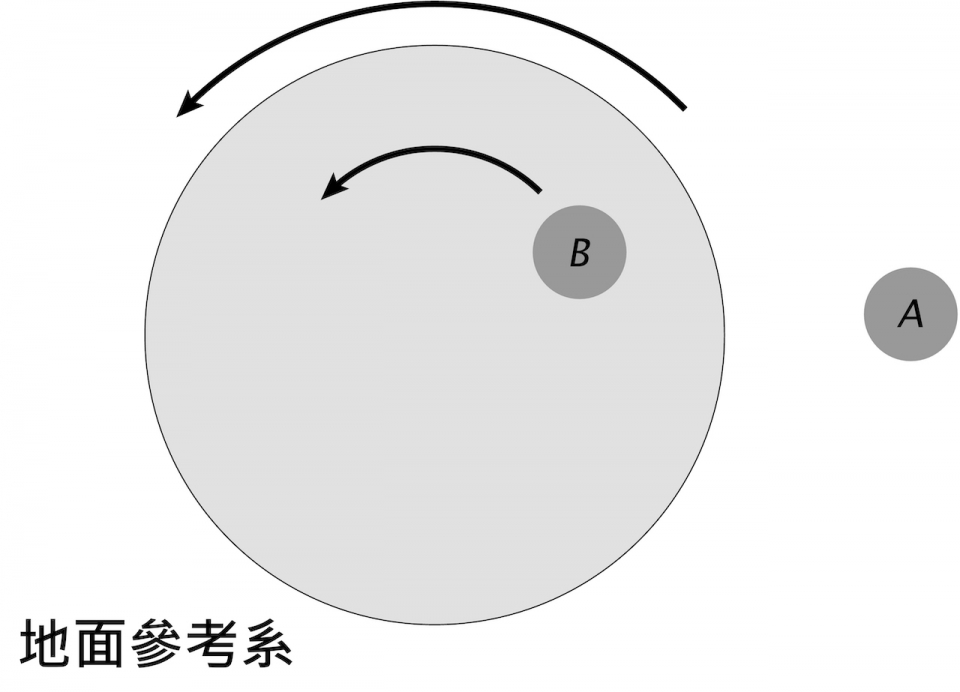
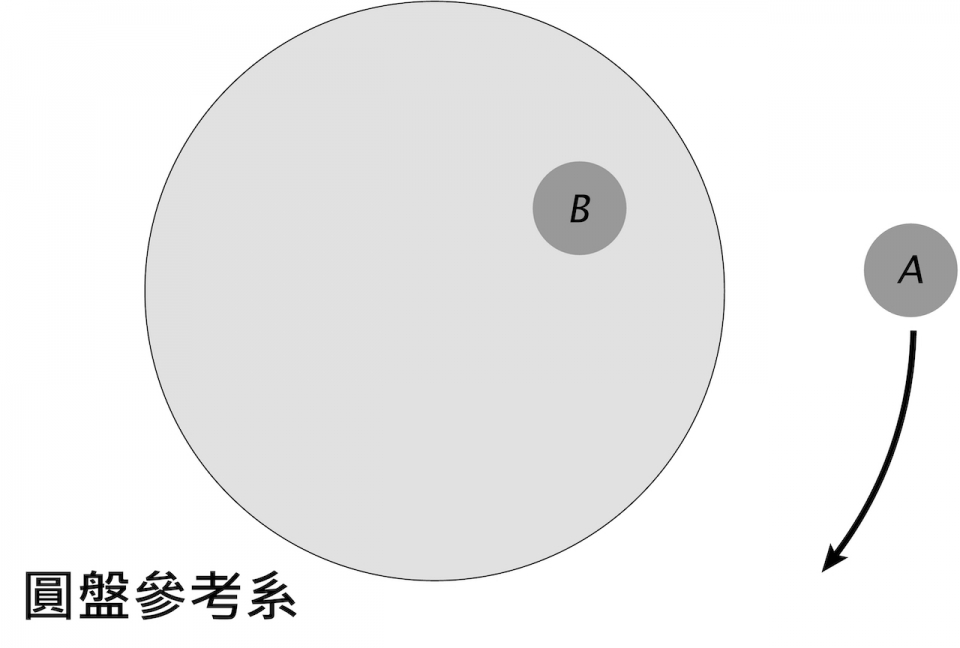
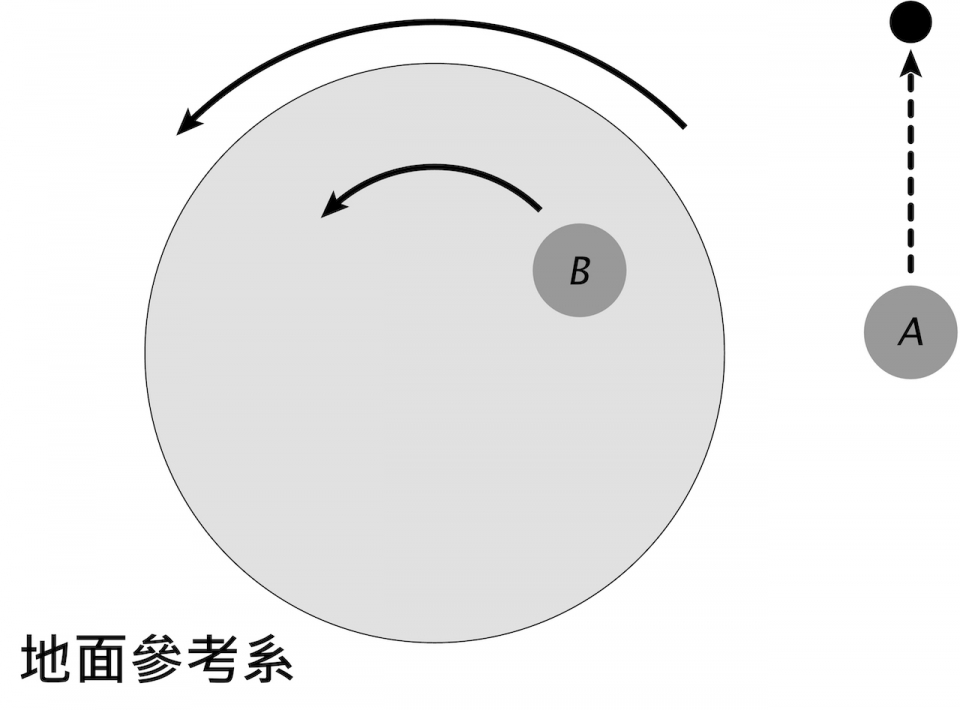
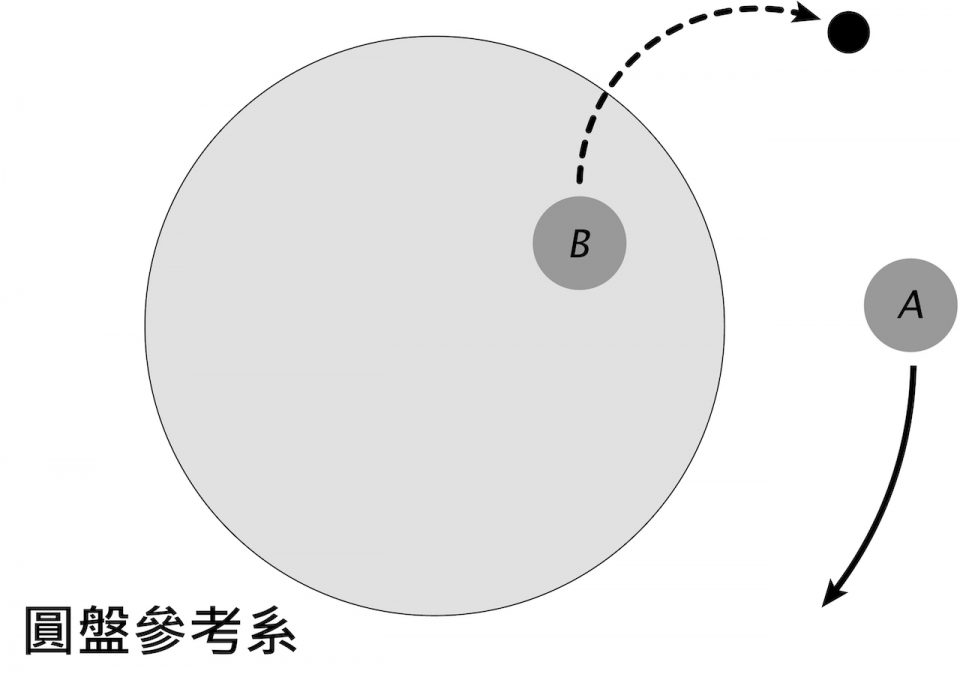
在牛頓力學裏，力學定律只適用於一種特別的參考系-----慣性參考系。在慣性參考系裏，一個不受外力作用的物體會作等速直線運動。牛頓力學假設了慣性參考系的存在，但並沒有對此作解釋。慣性參考系的存在是一個涉及物理學基礎的深刻問題，我們可用以下例子說明。設想兩人A和B，A站在地上，而B站在一旋轉圓盤上。在地面參考系，即A的静止參考系中，A是靜止的，而B跟圓盤一起旋轉，作逆時針圓周運動 (圖六)。在圓盤參考系，即B的靜止參考系中，B是靜止的，而A作順時針圓周運動 (圖七)。表面上看來，地面參考系和圓盤參考系是對稱的。可是，設想A和B各拋出一球。圖八顯示了在地面參考系中A拋出的球的軌跡，正如牛頓力學預言，由於球在水平方向沒有受力，球在水平方向以等速直線運動。圖九顯示了圓盤參考系中B拋出的球的軌跡，球雖然在水平方向沒有受力，但軌跡為一曲線，即球具有非零加速度，違反牛頓力學定律。所以，地面參考系與圓盤參考系並不對稱-----地面參考系是慣性參考系，而圓盤參考系是非慣性參考系。是什麼造成這種參考系的不對稱性呢？廣義相對論對此給出了答案。根據廣義相對論，慣性參考系即不旋轉的自由落體 (自由落體即只受到重力作用的物體) 的靜止參考系。對於慣性參考系，自由掉落即參考系的原點依時空短程綫運動 (也即時間軸被平行運輸)，不旋轉即三條空間座標軸被平行運輸。所以，參考系是否為慣性參考系取決於參考系的四條座標軸是否被平行運輸。正如我們在球面的例子看到，平行運輸是一種幾何概念，而時空的幾何結構由物質的能量和動量分佈決定。因此，參考系是否為慣性參考系取決於宇宙中質量在大尺度的分佈【註9】。例如，地球只受到其他星體的重力作用，所以是自由落體。如果忽略自轉，地球的靜止參考系便是慣性參考系【註10】。所謂不自轉，是相對於其他星體而言，包括太陽和眾多銀河系中的恆星，也包括其他星系中的星體，因為它們共同決定了地球附近的時空幾何結構。旋轉圓盤的旋轉也是相對眾多星體而言，因此圓盤參考系不是慣性參考系。

圖六

圖七

圖八

圖九

 

也就是說，「慣性」這個概念取決於整個宇宙的質量分佈。這個結論十分驚人，但如果想深一層，便會明白箇中美妙的對稱性。我們試作以下思想實驗。如果宇宙中只有地球，那麼地球能自轉嗎？問題是，如果地球在自轉，那麼它是相對於什麼在轉？牛頓力學的觀點是地球相對於絕對空間旋轉。廣義相對論否定空間的絕對性，而時空的性質由物質的分佈決定。所以，如果宇宙中只有地球，地球便是慣性參考系，因此並没可能旋轉。那麼如果宇宙中只有地球和太陽又怎麼樣？假設起初地球和太陽都不旋轉，由於角動量守恆，如果地球旋轉，太陽也必以反方向旋轉。可是，由於太陽質量遠大於地球，太陽的自轉角速度遠低於地球，彷彿沒有轉動，近似一慣性參考系；而地球在相對於太陽在自轉，即相對於慣性參考系轉動，所以並非慣性參考系。如是者，我們可以設想把其他星體一個一個加入，而每一個星體的加入都重新決定了什麼是慣性參考系。
 

形象化地說，物質好像與時空之間有一種黏力，當物質旋轉時，時空也被帶着轉；而且物質質量愈大，這種“黏力”便愈大。這個現象稱為慣性系拖拽 (inertial frame dragging)。慣性系拖拽在2011年被Gravity Probe B實驗證實【註11】。關於慣性系拖拽，讀者還可以嘗試解答以下一道非常有趣的思考題：忽略地球自轉，考慮一相對於地面在旋轉的一桶水。使水面分子作圓周運動的向心力由水壓提供，因此水面呈一曲面 (圖十)。現在假設水桶並沒有相對於地面旋轉，但宇宙中所有天體環繞着地球以相同方向作圓週運動，即整個宇宙環繞着地球旋轉。那麼，究竟水桶裏的水面會是平面還是曲面？ (答案見【註12】。)
 

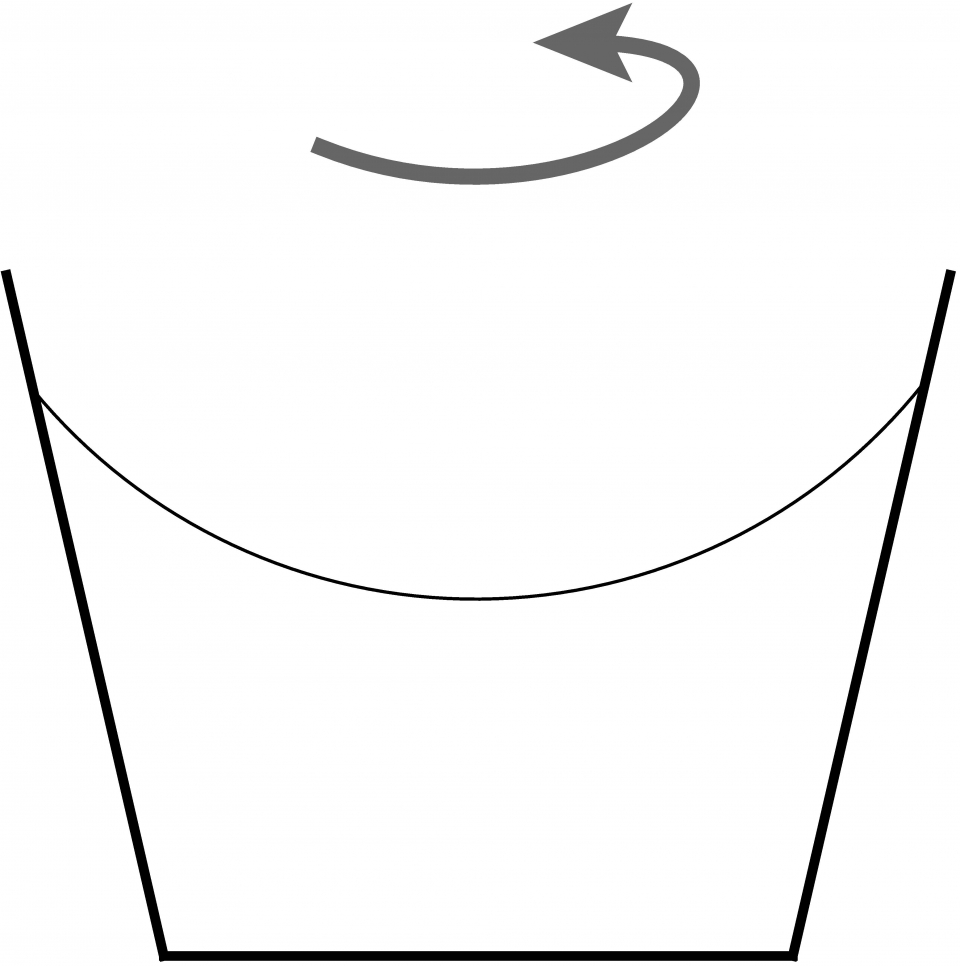
圖十

黑洞

如果物體的質量密度極大，重力大到所有其他交互作用也無法與之抗衡，物體便會無止境塌縮。隨着物體塌縮，物體的質量密度越來越大，鄰近的時空被嚴重扭曲，最後重力大到連光也不能逃脱。這時，物體的附近會出現一個球狀範圍，一但物質進入了該範圍，便永遠不可走出該範圍。這個球狀範圍稱為黑洞。圖十一顯示了大質量恆星在燃料耗盡後重力塌縮的時空圖，縱軸是時間軸，横軸是離恆星中心的距離，灰色陰影是恆星的物質，實線是事件視界(event horizon)，即黑洞的表面。從圖可見，隨着恆星塌縮，黑洞在時間出現。隨着恆星的物質掉進黑洞，黑洞的半徑增大，直至恆星的所有物質都掉進了黑洞。根據廣義相對論，事件視界的面積不可能隨時間減少，因此黑洞一但出現，便會永遠存在，不會消失。至今，多個天體已被推斷為黑洞。例如，我們已有大量證據推斷銀河系中心有一個四百萬倍太陽質量的超大質量黑洞。

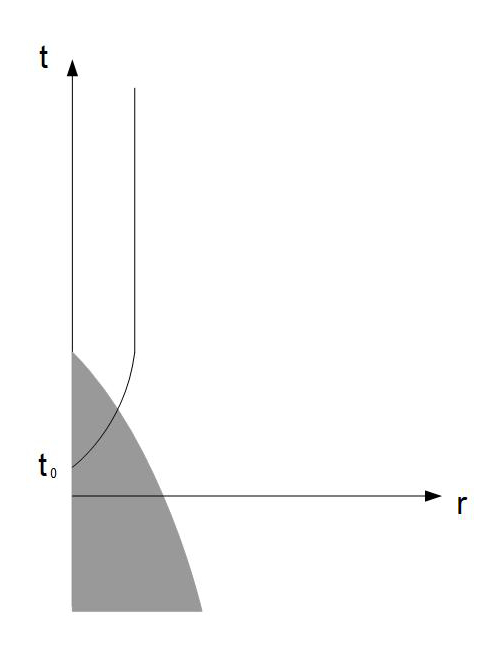
圖十一

重力波

電磁場的擾動會在空間傳播，形成電磁波。類似地，重力場的擾動會在空間傳播，形成重力波。由於重力埸對應彎曲的時空，重力波好比時空的漣漪。2015年，美國的雷射干涉重力波天文台 (LIGO) 量測到由13億光年以外兩個約30倍太陽質量的黑洞因碰撞而產生的重力波，首次證實了重力波的存在。由於重力波源十分遥遠，該實驗必須能探測到干涉儀中反射鏡的極微小擾動，準確度須達到質子半徑的千分之一 (~10⁻¹⁸ m)。重力波的測量將有助我們了解宇宙中如黑洞和中子星等高密度天體的物理特性。

 

重力子和量子重力

廣義相對論是一個經典理論，並沒有考慮量子效應，只適用於描述宏觀的重力現象。由於我們知道微觀的物質粒子由量子力學描述，而物質粒子間存在重力交互作用，重力交互作用在微觀尺度下必須遵從量子力學【註13】。因此，正如電磁場由光子組成，重力埸由重力子組成；正如光子傳遞電磁交互作用，重力子傳遞重力交互作用。類似電磁交互作用，重力交互作用也是一長程交互作用，所以重力子質量為零 (論證見第五章)。根據量子埸論，重力子自旋為2。有趣的是，自旋為2，質量為零，傳遞長程交互作用的粒子必須為重力子 (即交互作用荷是能量和動量)。這是一個極妙的定理。這意味着，即使我們從來不知道重力的存在，不認識廣義相對論，只認識平直時空 (狹義相對論) 和量子力學，那麼我們可以在此基礎上發展量子場論，而量子場論中的自旋為2的零質量粒子，如果能傳遞長程交互作用，便是重力子，即其組成的量子場的統計期望值滿足廣義相對論中的重力場方程。也就是說，量子場論預言了重力交互作用的可能性。可是，由於重力子交互作用極之微弱，要探測到重力子的存在，以現時的科技是不可能的。
 

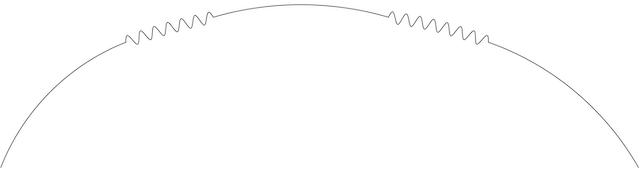
量子場論對重力場的描述只限於弱重力場 (ε ≪1))和低能過程 (涉及粒子的能量交換遠小於普朗克能量 (Planck energy)~10¹⁹ GeV)。這是因為量子場論建基於狹義相對論，即假設時空平直，而重力子代表平直時空的微小擾動 (如圖十二，其中的線代表時空，微小擾動代表重力子)。在強重力場 (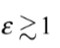)的情況下，時空嚴重扭曲，違反了平直時空的假設。可是，如果我們只考慮给定彎曲時空的微小擾動 (如圖十三)，那麼，對於微小的擾動來說，給定的背景彎曲時空 (即使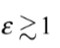)在局部近似平直，所以量子場論仍然成立。這種彎曲時空的量子場論有一驚人結論：黑洞會發放輻射，稱為霍金輻射 (Hawking radiation)。這意味着黑洞會因發放輻射而質量減少，而事件視界的面積也隨之而減少，直至最後黑洞消失。以上我們提到，根據廣義相對論，事件視界的面積不會減少，因此霍金輻射是純粹量子效應。霍金輻射是熱輻射，所以每一個黑洞都有非零溫度。有趣的是，黑洞的温度與其質量成反比，而宏觀黑洞的溫度都低於宇宙微波背景輻射 (2.73 K)。所以現實中的黑洞只會從比自身更高溫的環境吸熱。更何況，現實中的黑洞附近都有大量高温物質正在掉進裏面，這些物質本身會發放大量熱輻射。所以，要觀察到霍金輻射基本上是不可能的。

圖十二

圖十三
 

可是，如果我們嘗試用已知的物理學推敲宇宙的最終命運，霍金輻射便扮演着重要角色。星體間因重力吸引力而互相環繞運動，這會造成隨時間變化的時空擾動，所以會產生重力波。重力波會帶走能量，導致星體之間的距離隨時間減少。所以，在遥遠的未來，所有物質都聚集在一起，巨大的質量產生强大的重力場，導致物質塌縮成黑洞。這時，宇宙只有黑洞和背景輻射。隨着宇宙澎漲，背景輻射的温度會下降。當背景輻射的溫度低於黑洞的溫度，黑洞便會發放霍金輻射，質量隨之而減少，最後消失。所以，所有黑洞到最後都會蒸發消失，而宇宙中只剩下背景輻射，即光子。這便是現今我們對宇宙終於命運的推敲。

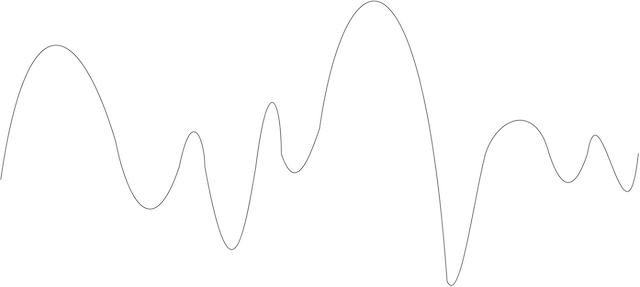
如果粒子之間的交互作用涉及極大的能量交换，交換的能量達到普朗克能量的數量級 (10¹⁹ GeV)，那麼時空在極小尺度也嚴重彎曲 (如圖十四)。在這樣的情況下，由於時空擾動極大，不可能把擾動解釋為重力子。也就是說，量子場論並不適用。我們需要一套全新的量子重力理論來描述這種極高能的粒子交互作用。現今的粒子加速器中的粒子碰撞能量最高只達10⁴ GeV。在可見的未來，實驗室無可能觀察到普朗克尺度的粒子現象。可是，根據我們現時對宇宙演化的認識，宇宙起源於大爆炸 (Big Bang)。大爆炸的一刻是時空奇點，即時空曲率和能量密度無限大 ，粒子的能量超越普朗克能量。所以，要了解大爆炸的一刻，我們需要了解量子重力。類似情況也出現於同樣是時空奇點的黑洞中心。量子重力是理論物理學的一個未解決的問題。現今最流行的量子重力理論是弦論 (string theory)。由於量子重力理論難以以實驗驗證，並且其基礎具爭議性【註14】，我們將不會對此作詳述。
 

圖十四

註解：

1. 如果把光速 c 定為 1，那麼一顆粒子的能量 E、質量 m 和動量 p 有關係 E²= m²+p²。E、p 與粒子的速率 v 有關係 p = Ev 。所以,當粒子的速率遠小於光速時 ( v ≪1), p ≪ E 並且 E ≈ m。
2. 四維時空的曲率有20個獨立分量，其中10個分量記錄了關於短程綫長度的資訊，稱為里奇曲率 (Ricci curvature)；另外10個分量記錄了關於短程綫之間角度的資訊，稱為外爾曲率 (Weyl curvature)。在廣義相對論裏，時空的里奇曲率正比於物質的能量密度、動量密度和動量流密度。這就是廣義相對論的核心方程-----愛因斯坦埸方程的內容。注意，這並不表示星體間的真空空間曲率為零，因為即使里奇曲率為零，外爾曲率一般不為零。例如，重力波在真空中傳播，對應的外爾曲率並不為零，但里奇曲率為零。
3. 球面上的大圓即球面上的一條半徑為球體半徑的圓形曲線，它把球面剛好分成兩半。
4. 這是弱重力場下的近似結果，適用於太陽附近，但對如黑洞附近的強重力場不適用。
5. 以現今物理學的標準看，愛丁頓的觀察數據並不理想。可是，這項實驗之後已被多個團隊重做，結果皆與廣義相對論的預言吻合。
6. 嚴格來說，要牛頓重力理論成立，除了要求ε ≪1，還要求物質的運動速度遠小於光速。
7. 宇宙在大尺度下的均匀性，可從宇宙微波背景輻射的探測得知。
8. 研究宇宙演化的物理學分支稱為宇宙學 (cosmology)。現代的宇宙學標準模型根據癀
   義相對論，在假設宇宙在大尺度下均匀和各向同性的前提下，以數個 (最多12個) 參數成功解釋了多項觀測數據，如宇宙微波背景輻射的微小不均匀性及其分佈，以及宇宙中質量的大尺度分佈等。
9. 「慣性系由宇宙中一切星體共同決定」由十九世紀物理學家和哲學家馬赫 (Ernst Mach) 提出，愛恩斯坦稱之為馬赫原理。雖然馬赫並沒有提出馬赫原理的數學形式，但該原理的物理意義極其深刻，顛覆了牛頓的絕對時空觀，是愛恩斯坦發展廣義相對論的重要導引。
10. 嚴格來說，參考系是一局部概念，所以慣性參考系的概念也只適用於參考系原點附近的極小鄰域。所以，即使忽略地球自轉，我們也只能說地球的中心是慣性參考系。在廣義相對論裏，由於時空中的短程綫被視為真正的「等速直線運動」，重力本身不被視為一種力，而重力的作用只是改變時空中「直線」的意義。在這種理解下，地面參考系並非慣性參考系，因為在該參考系中自由掉落的物體會向地心加速，即物體在沒有受力 (重力不算作力) 下加速運動。當然，這並不影響我們對地面上的旋轉圓盤和拋球軌跡的討論，因為我們只討論到水平於地面方向的運動。
11. Gravity Probe B是一組放在人造衛星上的高速旋轉陀螺。陀螺沒有受外力矩，並且跟人造衞星一起作自由掉落運動。根據牛頓重力理論，慣性系獨立於物質分怖，由於陀螺的自旋角動量守恆，陀螺的自轉軸恆久指向同一方向。根據廣義相對論，陀螺的自旋角動量在時空中被平行運輸，而地球的存在及自轉影響着附近的時空曲率，從而影響着平行運輸，因此陀螺的自轉軸隨時間改變方向。Gravity Probe B的實驗團隊於2011年發表了他們對實驗數據的分析結果，結果證明陀螺自轉軸的偏轉率與廣義相對論的預言吻合。
12. 是曲面。一切運動只有相對意義，没有絕對意義。水桶在旋轉並且星體靜止，與水桶靜止並且星體圍繞水桶旋轉，是沒有分別的。
13. 這種論點假設量子力學適用於任意小尺度。量子重力效應只在尺度小於10^-35 m 時才顯著。而現時實驗能考察的最小尺度約為10^-19 m。所以，我們現時並沒有證據顯示量子力學在尺度小於10^-35 m 時還適用。
14. 隨了弦論，量子重力的另一可能理論是廻圈量子重力 (loop quantum gravity)。此外，也有一說法是量子場論適用於任意小尺度，其必要條件是重力的漸近安全性 (asymptotic safety)，意思是即使在無限高能量下，時空的擾動仍然是有限，導致重力子的詮釋適用於任意小尺度。最後，當然也有說法提出量子力學在極小尺度下不適用。

延伸閱讀：

粒子物理行系列文章