在上一章，我們介紹了古典物理學中的最小作用量原理。根據該原理，一切物理過程皆可解釋為作用量S在給定邊界條件下取最小值。可是，根據量子力學，物理過程是隨機的，遵從特定機率分佈。我們在第一章知道，這機率分佈由波函數的平方給出，而波函數的演化遵從薛丁格方程式。類似牛頓運動方程，薛丁格方程式是一種對物理過程在時間軸上的局部描述。正如古典物理學中的最小作用量原理，在量子力學裏我們也可從整體角度描述物理過程，這種方法稱為路徑積分 (path integral)。在量子場論裏，我們會常用一種稱為費曼圖的圖像方法描述粒子的相互作用。路徑積分的概念是理解費曼圖的基礎。
 

路徑積分

讓我們先考慮最簡單的例子------一顆自由粒子的一維運動。設粒子在時間t₁有一確定位置x₁。那麼，該粒子於時間t₁的波函數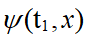是一個位於x₁的窄峰 (圖一)。當然，根據測不準原理，由於粒子的位置十分確定，粒子的速度極不確定，所以粒子的位置會隨時間變得愈來愈不確定。粒子於時間t₂=t₁+∆t的波函數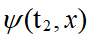如圖二，是一個擴展了的峰。波函數於時間t₂在位置X₂的值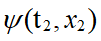的平方正比於粒子於時間t₂出現在位置x₂的機率。我們稱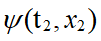為粒子從時空座標(t₁,x₁)到(t₂,x₂)的振幅(amplitude)，記為〈t₂,x₂|t₁,x₁〉，或簡單記為M。在t-x面上，連接(t₁,x₁)和(t₂,x₂)的路線有無窮多條 (圖三)。每條路線n均對應一作用量S的值，記為S_n。我們在上一章知道，自由粒子的作用量為

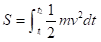
其中m粒子質量，v為粒子速度。振幅M的值由以下無窮求和給出:

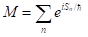
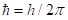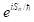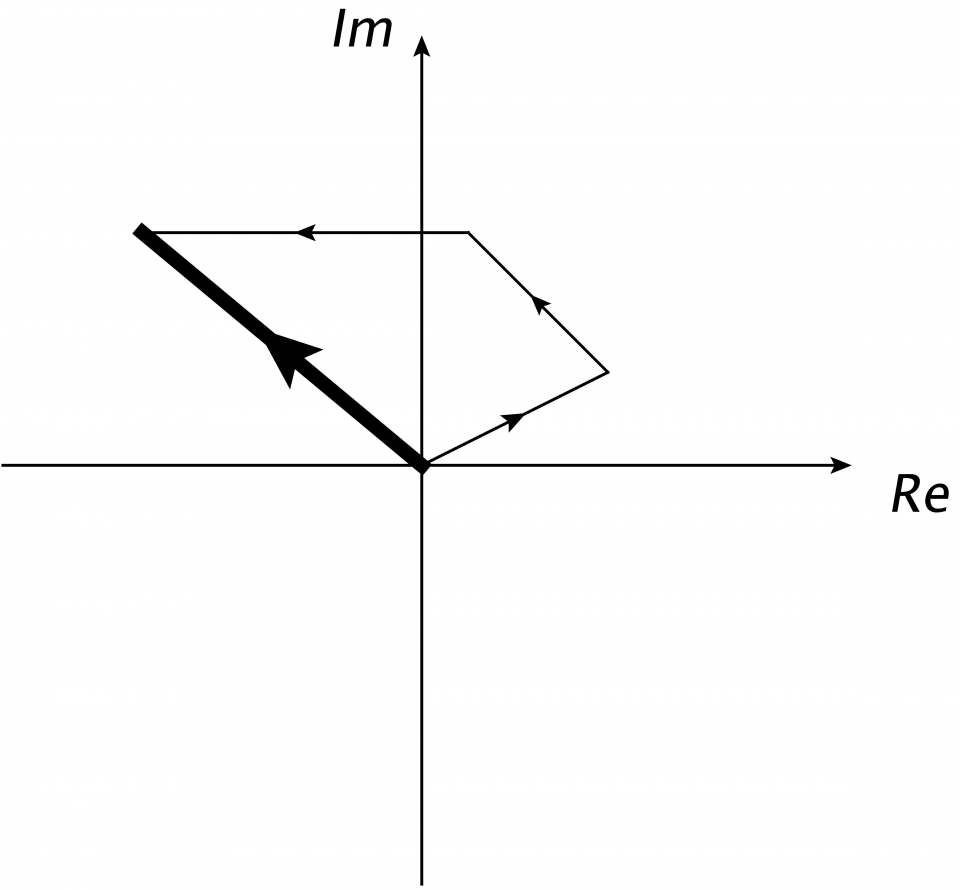
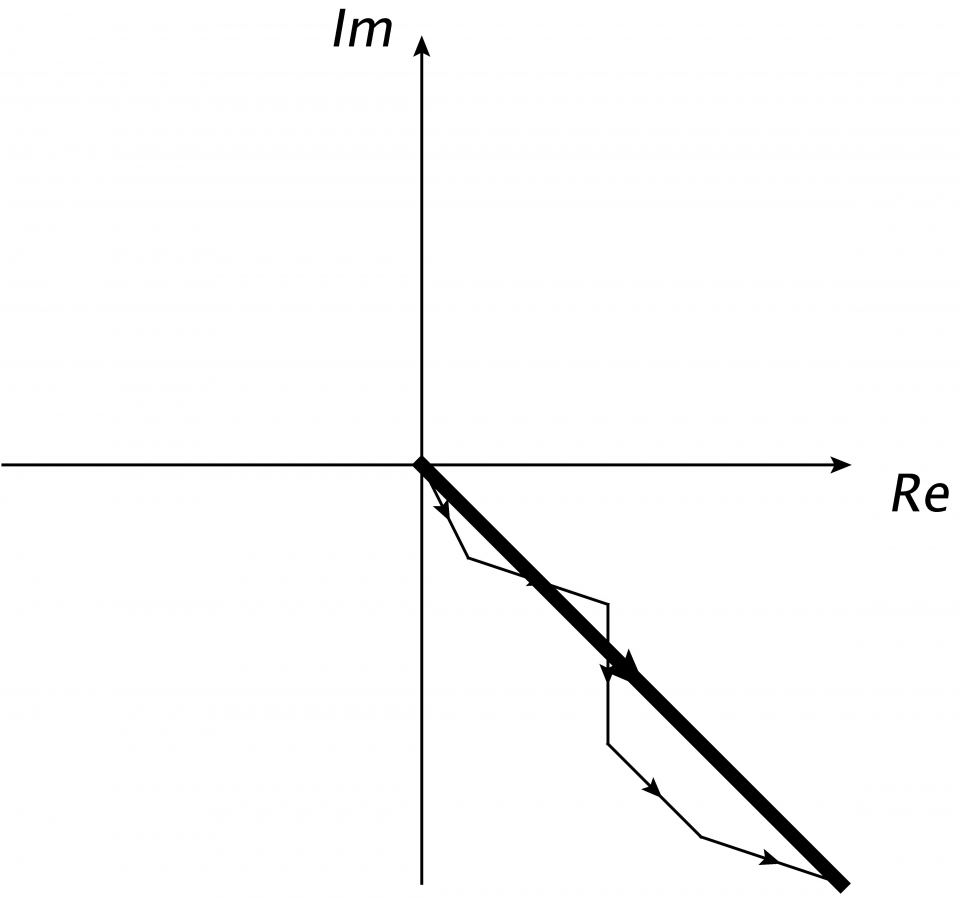
其中是約化普朗克常數。也就是說，每條可能的路徑n均對M有貢獻，而貢獻的值為模長為1的複數。這種對振幅M的計算方法稱為路徑積分 (path integral)。路徑積分是一種對物理過程的整體描述，因為作用量是路徑的整體性質。由於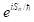是一模長為1的複數，我們可以把每條路徑的貢獻視為複平面上一長度為1的向量，而路徑積分則對應這些向量的和。圖四顯示了這種對路徑積分的圖像理解，其中每個細箭頭均代表一路徑的貢獻，而粗箭頭則代表幾條路徑的總貢獻。

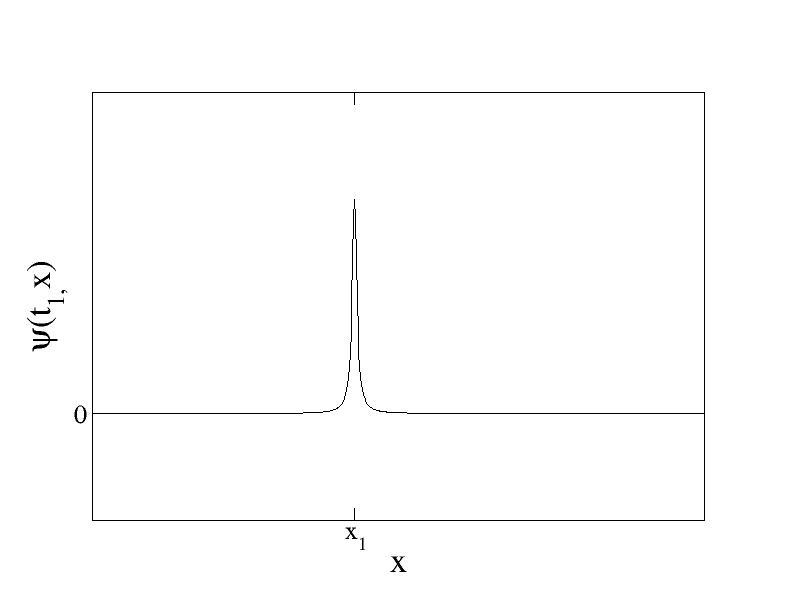
圖一

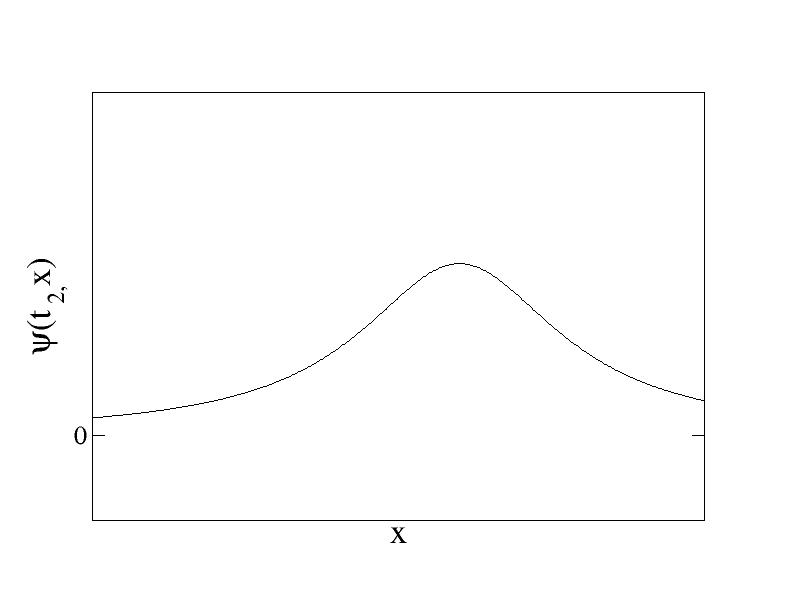
圖二
 

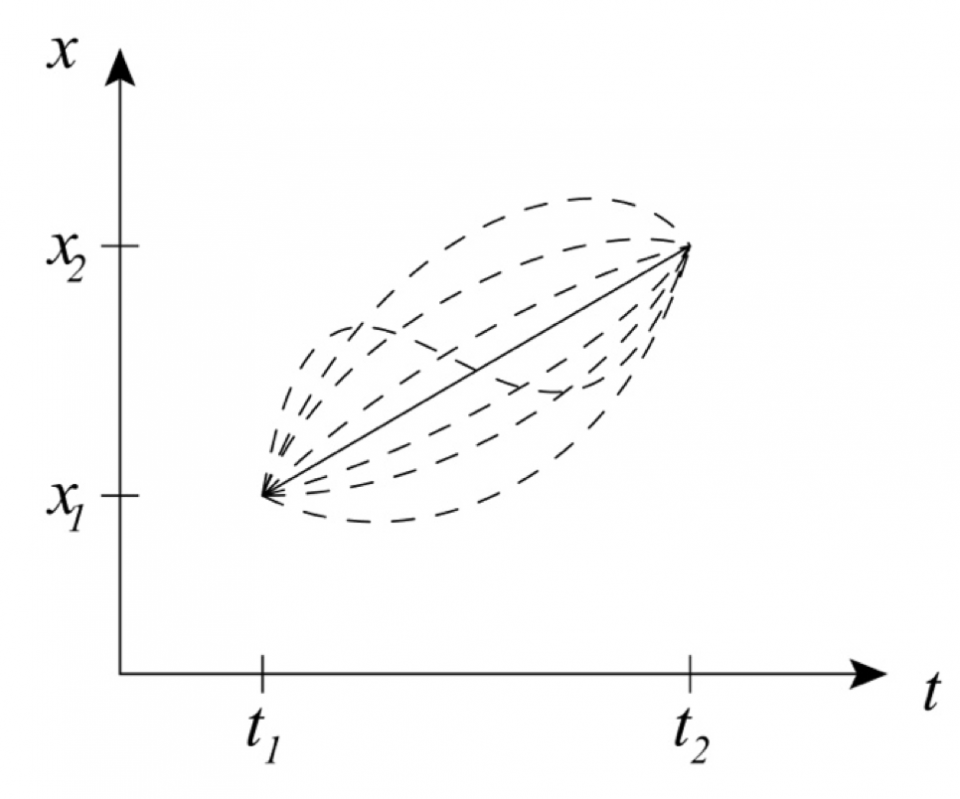
圖三
 

圖四

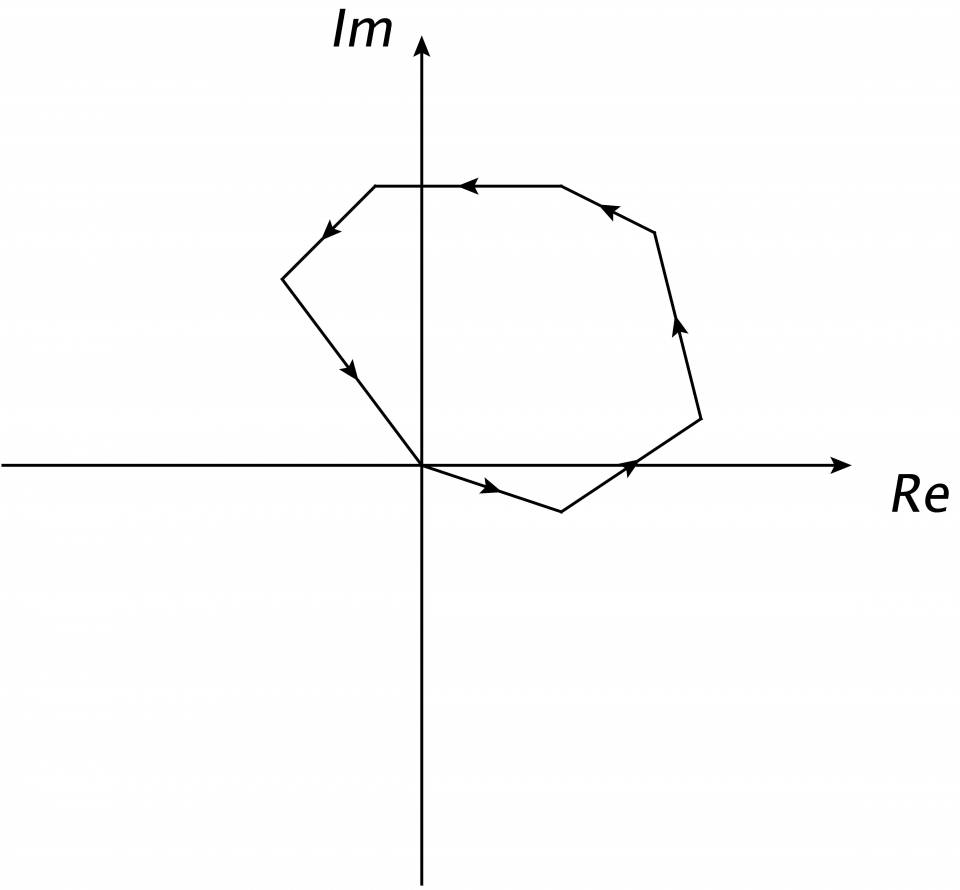
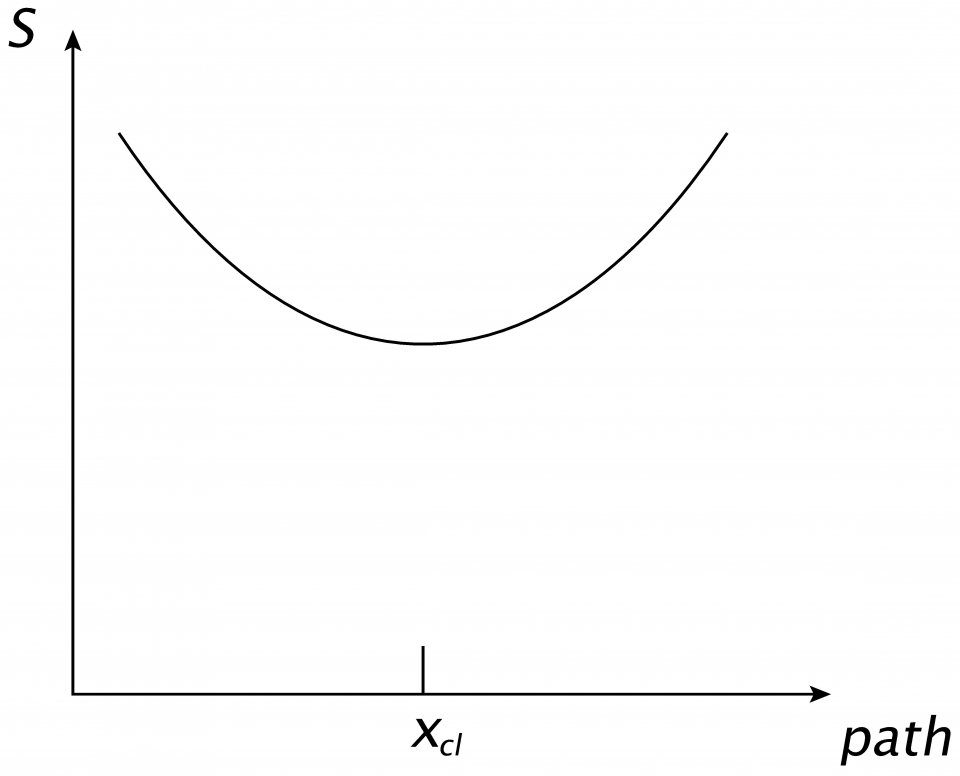
在上一章裏，我們知道，在古典物理裏，自由粒子以等速運動，如圖三中的實線，並且等速運動對應最小作用量。從量子力學的角度看，這是路徑積分的宏觀表現。對於宏觀物理過程，由於涉及的質量和時間尺度大，作用量遠大於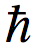，而由於函數e^iθ具有週期2π，很多路徑的貢獻互相扺消 (如圖五)。對於作用量最小的路徑 (圖六中的x_cl)，鄰近的路徑具有相近的作用量數值。這導致x_cl附近路徑的貢獻互相建設性叠加 (constructive interference)(如圖七)。所以，對於宏觀物理過程，只有作用量為最小的路徑在路徑積分中有非零貢獻。這就解釋了為何宏觀現象遵從古典物理的最小作用量原理。
 

圖五

                   圖六                                    

              圖七

對於非自由粒子，正如上一章所述，我們只須把作用量的形式稍微改變。例如，如果粒子受的力Ｆ由勢能Ｖ(x)給出 (F=-dV/dx)，那麼粒子的作用量便為

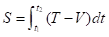
其中T=1/2mv²為粒子的動能。更一般地，對於所有古典物理中的系統，如多粒子系統和電磁場，它們在量子力學中的振幅也可由路徑積分給出，其中涉及的作用量與古典物理中的作用量形式相同。在路徑積分的框架下，物理學的基本原理歸結為作用量的形式。我們會在將來看到，作用量的形式由相互作用的對稱性決定。
 

再看雙縫實驗

在第一章，我們討論過雙縫實驗。我們可以以路徑積分的角度直觀地了解電子在雙縫實驗中的波動性。如圖八，電子從P點出發，而最終落在Q點的機率由振幅的平方給出。振幅由路徑積分給出，因此所有連接P點和Q點的路徑均須被考慮在內。電子可能經過狹縫A或B，所以這兩種路徑都對振幅有貢獻。這就解釋了為何電子能像波一樣同時穿過兩個縫。
 

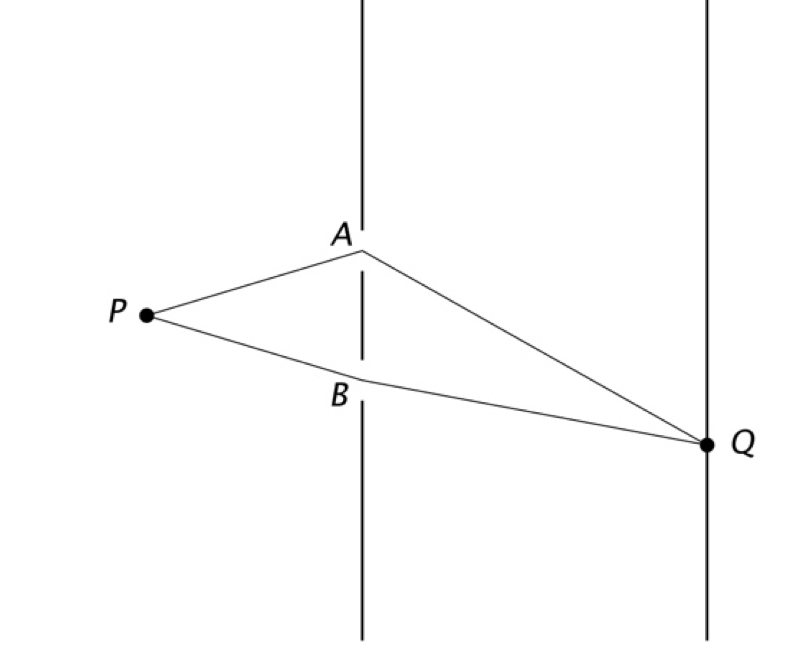
         圖八

一些歷史

路徑積分的始創人是理查德·費曼 (Richard Feynman, 1918-1988)。費曼是二十世紀最具影響力的物理學家之一，在理論物理的多個範疇作出了重大貢獻。費曼生於美國紐約市的一個猶太家庭，父親是一位商人。費曼自小熱愛科學，於小學時會在家中修理收音機和自製防盜警鐘。於中學時，他自修了一些高等數學。費曼在麻省理工學院修讀物理學本科。在這段期間，他在全美大學數學比賽Putnam Competition中獲得冠軍。

1939年，費曼考進普林斯頓大學攻讀物理學博士。那時的普林斯頓羣龍雲集。費曼的論文導師是約翰·惠勒 (John Wheeler)。費曼於普林斯頓的第一次研討會中，出席的有愛因斯坦(Einstein)、包立 (Pauli) 和馮·諾伊曼 (von Neumann)。惠勒是位思想開放的年青物理學家，勇於接受和嘗試新主意。為了解決電動力學中帶電荷質點因自相互作用產生的質量無限大問題，費曼和惠勒發展了一套全新的電動力學，其中帶電荷質點並沒有自相互作用。為了把這套新理論量子化，費曼需要一種全新的量子化方法。狄拉克 (Dirac) 寫於1932年的一篇論文《The Lagrangian in Quantum Mechanics》啟發了他。在該論文中，狄拉克成功把振幅寫成路徑積分的形式。可是，狄拉克只寫下了形式，並沒有展示怎樣以路徑積分作實際計算。由於每一路徑為一時間函數，路徑空間是一無限維空間。所以路徑積分是一個對無限多個變量作的積分，實際計算並不容易。費曼克服了這些困難，發展了一套計算路徑積分的技巧。這些成果成為了他的博士論文-----《A New Approach to Quantum Theory》。費曼於1942年獲得博士學位。

費曼是粒子物理和量子場論發展史中的核心人物，我們在以後會繼續聽到很多關於他的故事。值得一提的，是他的獨特個性和數學才華。費曼很重視內容，鄙視形式。他曾強調父親在他小時候已告訴他：「無論你能用多少種語言稱呼一種鳥，你對該種鳥仍是一無所知。」在他於中學時自學高等數學的筆記中，不難發現文法錯誤和拼字錯誤。在普林斯頓大學研究院的入學試中，他在物理卷和數學卷中取得前所未有的高分，但歷史和語文的分數很低。費曼不常提到自己的數學才華，但他絕對是解決數學難題的高手。他在高中的最後一年，在紐約大學數學錦標賽中勝出，並且分數遠高於其他參賽者。費曼在本科時參加的Putnam Competition是全美本科生的數學比賽，參賽者不乏頂尖大學中的數學系高材生。他作為物理系學生，擊敗了多位未來數學家，獲得了冠軍。費曼發展的路徑積分和費曼圖，本身就是一門數學，其中隱藏的數學結構到現今仍是數學研究的熱門課題。





延伸閱讀：

粒子物理行（三） 作用量

粒子物理行（五） 四種基本力 ----- 電磁交互作用