
SIR!我們用南部力學模擬傳染病吧!
- 物理新新聞
- 撰文者:文裕
- 發文日期:2020-05-27
- 點閱次數:1390
為了衡量疾病的傳染性,科學家提出了「基本傳染數 R0」,具體是這樣計算的..
R0= 每次與健康的人接觸的傳染概率 p× 染病時每單位時間與健康的人的接觸次數 c× 染病時長 t
百年前的西班牙流感的 R0 是 2~3,即是平均每個患者會傳染給 2 至 3 人,而麻疹則高達 12~17 人!按照這 R0 的意義,對於 R0 = 2 的疾病而言,它的傳播狀況是這樣的..
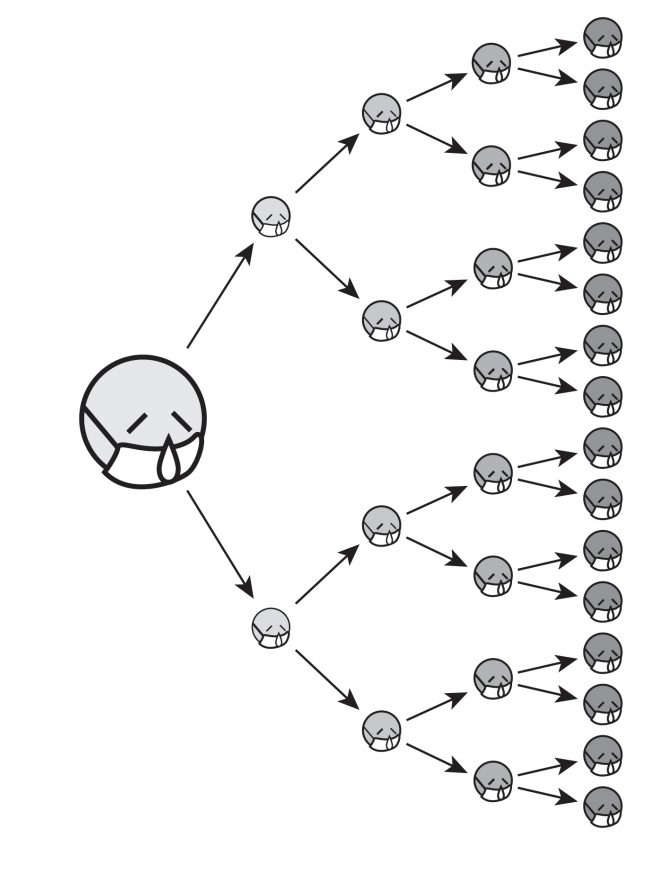
也就是說,即使一種傳染性不強的病,32 個患病周期就能感染全人類嗎?
〝才不會。〞
首先,當人們注意到某疾病的傳播時,人們會採取措施以減低患病風險。例如病人會被隔離 ( 減少式中的 c),人們會使用口罩等防護裝備 ( 減少式中的 p)。甚至,即使該地區的人什麼都不做,傳染率還是會下降,因為健康的人越來越少。
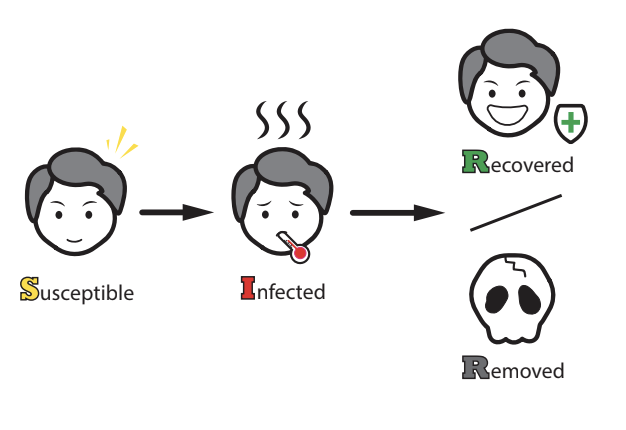
所以,Sir,我們不能用指數律來模擬傳染病的。我們用 SIR 模型吧!
這裡的 S、I 和 R 分別指的是
S = 健康人數
I = 感染人數
R = 康復或死亡人數
而 SIR 模型的公式長這樣..
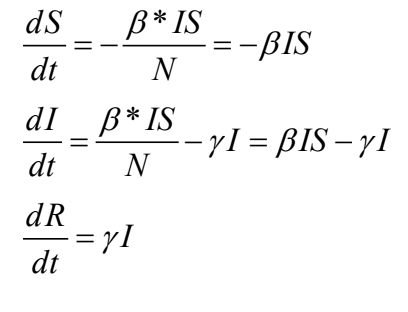
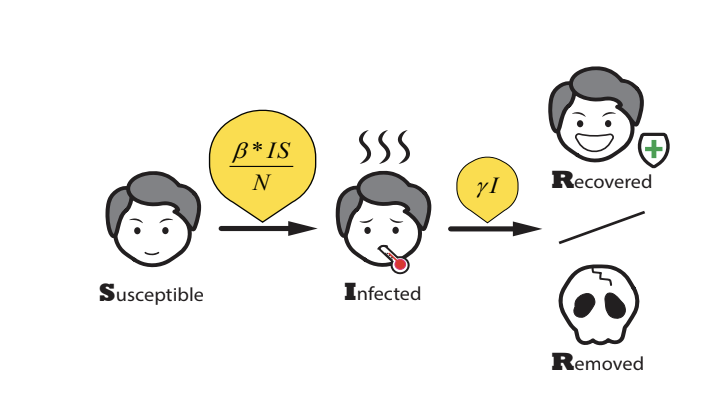
其中 N=S+I+R是總人數(包括不幸病故的人),而 β*是感染率。為方便起見, β*/N會記為 β ,即每單位人口感染率。由於感染是由健康的人和病人接觸造成的,所以感染率( dS/dt 的絕對值)與感染人數 I 和健康人數 S 成正比。每單位時間的康復人數( dR/dt )與染病人數成正比,γ 為復原率。因此SIR模型是個很直觀的簡單模型。
然而要讓 SIR 模型更貼近現實,我們可能要讓係數 β ( 感染率 ) 和 γ ( 復原率 )隨時間變化,( 例如冬季時流感的 β 普遍較大 );又可能要考慮不同地區之間的交通和隔離等等。這麼一來,模擬的複雜程度又更高了。
為了使模擬更精確更貼近現實,物理學家提供了非常多的主意,其中一個是利用「南部力學」來模擬。
修但幾咧,「南部力學」?研究野豬和多糖的珍珠奶茶的力學?有沒有「北部力學」? 南部力學事實上是南部陽一郎(Yoichiro Nambu) 所提出的一種哈密頓力學的推廣。
當我們學牛頓力學,我們會直觀地認識「力」,然後再利用牛頓定律列出運動方程來研究系統的演化。例如單擺運動中,我們會考慮單擺受的力,再利用F = ma 計算單擺的位置如何隨時間演化。
至於哈密頓力學,它的奠基概念不是力,而是哈密頓量 H,在不少情況中,H= 動能 K+ 勢能 U。當我們選定了用什麼座標系統後,利用這公式就能寫出關係式模擬系統的演化..

這裡 q 是你選定的坐標,p 則是對應的動量。如果對哈密頓力學不熟悉,可以參考這裡的例子。
我們挑選 θ 作為座標。由於座標是一隻角,所以 p 就是角動量。那麼
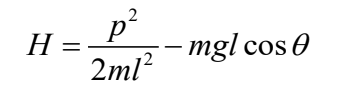
運動方程就能寫成..
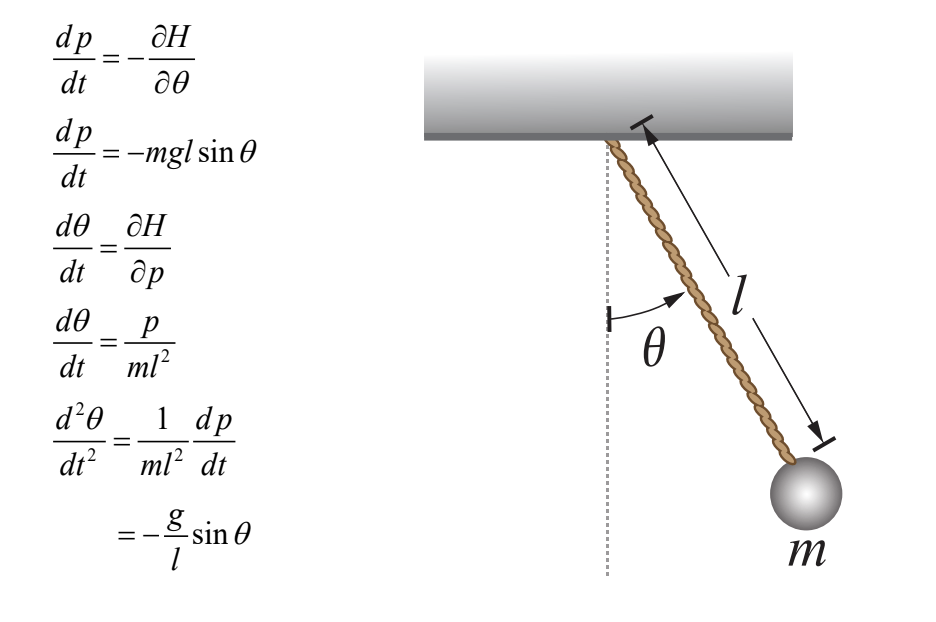
哈密頓力學有明顯的特徵,就是一個系統中只有一個 H。而南部陽一郎所作的推廣,就是增加可以處理的 H。其實南部力學最初是用來研究剛體的力學。對於有兩個守恆量 H1 和 H2 的系統,南部陽一郎提出公式..
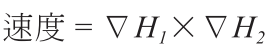
這條公式又可以怎麼用呢?
我們可以把一個地區的感染狀況當成一個在球面運動的質點,它的位置是
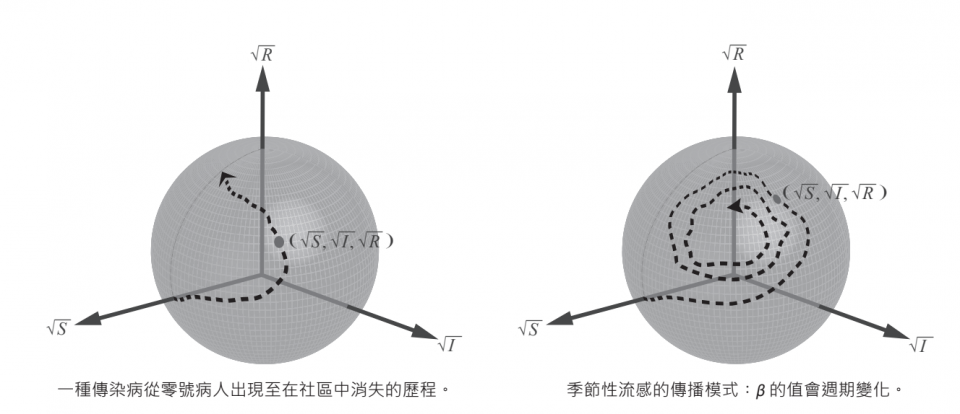
在 SIR 模型中,我們有這兩個守恆量..
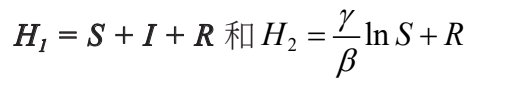
所以一旦我們知道 β 和 γ 兩個參數後,可以用這方程知道質點的瞬時速度..
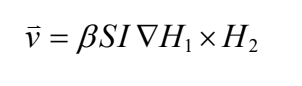
用這個方法模擬傳播的好處是,除了模擬一個封閉的社會中的傳播狀況,還可以模擬多個互相影響的社區。
作者:文裕
參考文獻
1.James Holland Jones (2007), “Notes On R0”, (unpublished) https://web.stanford.edu/~jhj1/teachingdocs/Jones-on-R0.pdf
2.Kazumi Omata (2017), “Nonequilibrium statistical mechanics of a susceptible-infected-recovered epidemic model”, Phys. Rev. E, 96,022404.
3.Yoichiro Nambu (1973), “Generalized Hamiltonian Dynamics” Phys. Rev. D, 7, 2405.