為科學而生 為原子而死的波茲曼(上) 帝國的黃昏

上一回的阿文開講，介紹了統計力學的開山祖師爺之一的吉布斯。這一次阿文要接著介紹另一位幾乎與吉布斯同時間在德語世界開創統計力學的大人物，他就是大名鼎鼎的波茲曼。與一生平靜無事，與人無爭的吉布斯相比，波茲曼的人生可以算得上是波瀾壯闊，為了說服別人相信自己苦心孤詣建構出來的理論，波茲曼終生與人爭論不休，最終居然抑鬱自殺，這樣的傳奇人物，阿文當然無法放過。就讓阿文仔細為您介紹這位來自維也納的物理大師的傳奇一生吧。

路德維希·愛德華·波茲曼（Ludwig Eduard Boltzmann）1844年生於維也納。他的祖父Gottfried Ludwig Boltzmann是一個自柏林移居至維也納的鐘錶製造商。而他的父親Ludwig Georg Boltzmann則是在拿到法律學位後，負責稅務相關的事務的帝國官員。他的母親Maria Katharina Pauernfeind則來自薩爾茨堡的一個富裕的商人家族。她的曾祖父還擔任過薩爾茨堡的市長呢。路德維希是家中長子，他有一位弟弟Albert 以及一位妹妹Hedwig。Albert 十六歲時死於肺結核，而Hedwig則是終身未嫁，四十二歲發狂而死。

圖片來源：https://commons.wikimedia.org/wiki/File:Boltzmann2.jpg
 

由於波茲曼的父親任所常常更換，所以路德維希的啟蒙教育是在家裡由家教來教他，直到十歲時他才到上奧地利的林茨就讀高中。他所讀的Akademische Gymnasium Linz 是一所標榜人文教育的學校，他的同學大部分都跑去念神學去了。據說大作曲家Anton Bruckner 年輕時曾教過路德維希鋼琴呢!(當時Anton Bruckner 在林茲擔任在教堂彈奏管風琴，直到1868年，Bruckner成功以通奏低音和對位法教授的身份到維也納音樂學院任教。) 他的家境在當時的奧匈帝國算是相當不錯的。 但是悲劇突然襲擊波茲曼家，路德維希的父親在1859年驟逝，享年五十七，所幸他的家庭財務由母親一手支撐，因為他母親的娘家相當富裕。但是四年後路德維希的弟弟又因肺結核過世，這對路德維希的心中投下難以抹滅的陰影。不過他還是強打精神，幾個月後以優異成績從高中畢業，之後他們舉家搬到維也納去。

波茲曼自1863年開始在維也納大學攻讀物理。維也納大學的物理系是1849年才由Christian Doppler 所創立的，大家都學過的都卜勒效應就是以Christian Doppler 命名。Doppler 在1853年英年早逝，所長一職由Andreas Freiherr von Ettingshausen 接任。他曾設計過電動機，其中應用了用於發電的電磁感應原理。此外他推動了光學的發展，同時還編寫了一本物理學教科書。他的授課方法在奧帝利影響力不小。此外，他還編寫了一本有關組合數學方面的書(1826年，維也納)。波茲曼在只比他年長九歲的Joseph Stefan的指導下於1866年十二月獲得博士學位。他的學位論文主題是氣體運動論。波茲曼在此也受教於數學家Josef Petzval 與 August Kunze。

當時的維也納是帝國的首都，從帝國的各角落來的人才都聚集於此，波茲曼的老師Joseph Stefan 就是出身於今天的斯洛凡尼亞 (當時在哈布斯堡家族的統治下，也是奧匈帝國的一部分)，除了是一位優秀的科學家之外，還是位詩人呢。而且他是以自己的母語斯洛凡尼亞語來創作的!而在1866年 Joseph Stefan 取代了年邁的Andreas Freiherr von Ettingshausen 成為維也納大學物理所的所長。同一年專精於氣體動力論的Josef Loschmidt 也來到維也納大學任教。 Stefan 完全投入科學研究，深受學生愛戴，波茲曼也不例外，它曾這樣讚揚過Stefan:

沒有東西可以減損先生傑出的德性與對年輕學者的魔力，他所施展的魔力只能意會 無法言傳！這魔力終身與我同在，它變成嚴肅卻又引人入勝的實驗活動的象徵！

獲得博士學位之後，波茲曼又當了兩年Stefan的助手。Stefan 是史上第一個測量氣體熱導率的科學家，他還特別研究了氣體的蒸發以及流體的擴散與熱傳導現象。結果發表於Untersuchung über die Wärmeleitung in Gasen, Zweite Abhandlung (1875)(英文 Investigation of Heat Conduction in Gases, Second Essay)。他還曾因光學的著作而得到維也納大學頒發的萊布尼茲獎。事實上，今天粒子在流體表面因蒸發作用而引發的流動就被稱為Stefan流。而且Stefan 是少數從一開始就認知到馬克斯威爾電磁方程式重要性的物理學家，他還曾算過線圈的電感並且指出馬克斯威爾計算錯誤之處。他也研究過高頻的電流可以穿透金屬表面的趨膚效應。當他在研究冰層如何在水上成長時解決了邊界會變動的微分方程的數學問題，這個問題最早是由Lamé 與 Clapeyron 在1831年開始研究的，現在這問題被稱為Stefan problems。結果發表在Über die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere ，英文About the theory of ice formation, especially about ice formation in the polar seas，1889)。但是論到Stefan最出名的工作還是在1879年他指出黑體輻射的輻射強度與黑體溫度的四次方成正比，而波茲曼則在1884年利用熱力學給出一個理論的推導。這個公式被稱為Stefan–Boltzmann law。Stefan利用這個定律配合法國科學家Charles Soret 的實驗數據而估計太陽表面溫度約5430 °C。這是對太陽表面溫度的第一個較精確的測量結果。當然，這些都是波茲曼畢業以後多年的事了。

由於Stefan的強力推薦，波茲曼於1869年七月受聘為Graz大學的教授。這個缺原先是著名的科學哲學家馬赫(Ernst Mach)的，他搬到布拉格大學之後才出缺。Graz大學是奧地利境內創辦時間僅次於維也納大學的大學。學校是在1585年由大公卡爾二世建立，同年交給了Societas Jesu來管理，它的目標是讓所有社會階層的人都有機會接受精英教育。1773年由帝國接管，它的目標是提拔勇於服務於國家的人，並向他們灌輸實用的知識。1827年它由皇帝Franz二世重建。在威廉·馮·洪堡的大學改革後大學引入了教學自由的觀念。大學宗旨變成是傳授知識，並將大學生帶入科學研究的世界。從此大學擁有了高度的自治。波茲曼二十五歲就當上了Graz大學數學物理的教授，算得上是少年得意。

當時普奧戰爭結束不久，普魯士的國勢蒸蒸日上，德意志的科學也人才輩出。波茲曼對維也納的師長們不願與德語世界的其他學者交流早就頗多微詞，所以他在1870年春天就到Heidelberg 拜訪Robert Bunsen, Gustav Kirchhoff 與Leo Koenigsberger等人。隔年他還去柏林拜訪Hermann von Helmholtz。就在這一年，波茲曼與Graz的一位有抱負的數學和物理老師，Henriette von Aigentler相遇。Henriette 在1854年出生於Stainz一個頗受敬重的家庭，但是她父親在她十歲時過世，她是由當時Graz市長Wilhelm Kienzl給予她財務的支持。當時奧匈帝國的大學不讓女性入學，她在試圖旁聽當地大學講授的課程時遭到拒絕。她在波茲曼建議下進行了申訴，並獲得了成功，成為Graz大學第一位女學生，主修數學與科學，輔修哲學。後來她與波茲曼陷入愛河，成為波茲曼的未婚妻。

令人驚訝的是，波茲曼在1873年又申請了維也納大學數學講座教授，他在八月成功拿到這個教職。除了數學之外，波茲曼也針對熱的力學理論開班授課。但是在維也納的時候，他在1875年九月二十七日寫信向Henriette 求婚，更令人驚訝的是到了1876年他又回去Graz,成為物理所的所長。1876年7月17日，他與Henriette von Aigentler正式結為夫婦。時年三十二歲。婚後他們育有三個女兒和兩個兒子。接下來他在Graz度過了十四年快樂的時光。他搬進了座落在Oberkroisbach 的一處豪宅，在這裡養兒育女，同時教書也卓然有成。Svante August Arrhenius和Walther Hermann Nernst都是這個時期他在Graz教過的學生。Svante August Arrhenius 是瑞典化學家。提出了電解質在水溶液中電離的阿瑞尼斯理論，研究了溫度對化學反應速率的影響，得出阿瑞尼斯方程。由於在物理化學方面的傑出貢獻，被授予1903年諾貝爾化學獎。Walther Hermann Nerns是德國化學家，他提出了熱力學第三定律，這條定律對化學親和力的計算尤其重要，他因此榮獲1920年的諾貝爾化學獎。所謂得天下之英才而教育之，波茲曼在Graz 應該是得其所哉。也正是在Graz，波茲曼逐漸醞釀他利用統計的方法將微觀的動力學與巨觀的熱力學聯結起來的宏偉構想。讓我們來看看他在Graz前後兩段時間(1869-1873,1876-1890)，波茲曼作了哪些劃時代的研究。

波茲曼一生深信不疑的是古典力學的有效性。他認為整個自然科學都應該奠基在古典力學之上。而十九世紀的六十年代最熱門的兩個問題，一個當然是電磁現象，而另一個則是如何從動力學來瞭解"熱"以及相關的現象。當時氣體動力論還是個嶄新的領域，而波茲曼的博士論文就是關於氣體動力論，他對如何從動力學來闡明熵以及如何用古典力學來"證明"熱力學第二定律特別感著迷。原本在熱力學中熵與溫度相彷 是一個只有操作型定義的巨觀的物理量，而且還是跟熱機的具體操作有關的一個意義曖昧的量: 簡單講是熱機在一個循環動作中輸出(或輸入)的功除以熱機的溫度。熵的概念是由德國物理學家克勞修斯於1865年所提出，他把這一狀態參量命名為Entropie（德語）（來源於希臘語τρoπή，en加上tropein是「內在的變動」的意思），他發現熱力學系統從一個平衡態到另一平衡態的過程中，其熵永不減少：若過程可逆，則熵不變；若不可逆，則熵增加。這就是有名的熱力學第二定律。以熱力學的術語，熱機是無法將能量做最完美的運用, 雖然能量是守恆的，但似乎愈來愈多能量會變成無法運用而耗損掉。這背後的微觀意義是什麼?這正是讓波茲曼念茲在茲的大哉問。

所謂思而不學則罔，波茲曼當然先從前輩身上學習，最重要的前輩是英國的馬克斯威爾了。從1868年到1871年，波茲曼陸續寫了四篇文章，都是與馬克斯威爾關速度分布函數有關。馬克斯威爾在1860年第一次推導出著名的馬克斯威爾速度分布函數，它解釋了許多基本的氣體性質，包括壓力和它的擴散性質。所謂的分布函數 (distribution function)是指當一個由多粒子所組成的物理系統處在溫度T時，在系統達熱平衡時，粒子處在某一速度狀態的機率分布。透過分布函數，科學家可以將巨觀的物理量”溫度T”與氣體動能聯接起來。由此我們才真正瞭解”溫度”的背後的物理涵義，在此之前， “溫度”只有操作型的熱力學定義。但是現在我們知道氣體的溫度與氣體粒子的平均動能成正比。更進一步，馬克斯威爾在1867年主張熱平衡狀態的分布函數應該是不變的，換句話說，粒子雖然不斷碰撞，但是分布函數卻不會改變，由此馬克斯威爾引入"分子混沌假設"(the molecular chaos hypothesis)，就是兩個粒子發生碰撞機率與兩個粒子的速度分布乘積成正比，而且與粒子的位置無關，由此他給出比之前更具一般性的證明。(事實上馬克斯威爾分布函數可以從馬克士威-波茲曼統計推導出來(1877)。馬克斯威爾-波茲曼統計是描述氣體分子等古典粒子的統計分布。所謂”古典粒子:是假設不同粒子間, 即便它們的物理性質完全相同,仍然可被分辨，也就是說可將所有粒子編號且每個粒子可用牛頓力學來描述其運動。當然在量子效應開始變的重要時馬克斯威爾-波茲曼統計就不再適用了。1926年Heisenberg 提出測不準原理之後人才理解到全同粒子是無法分辨的。)

Ludwig Boltzmann and co-workers in Graz, 1887. (standing, from the left) Nernst, Streintz, Arrhenius, Hiecke, (sitting, from the left) Aulinger, Ettingshausen, Boltzmann, Klemenčič, Hausmanninger
圖片來源：https://en.wikipedia.org/wiki/Ludwig_Boltzmann#/media/File:Boltzmann-grp.jpg
 

波茲曼第一個真正算得上具有原創性的貢獻是他在1868年發表的論文中將馬克斯威爾的推導推廣到系統受到外力的情況，但是值得注意的是波茲曼一開始將分布函數理解為一顆粒子在不斷因碰撞改變速度的歷程中，速度為v 的時間佔整個歷程的比例，馬克思威爾定義的分布函數則是在某特定時刻速度為v 的粒子佔全部粒子的比例並不一樣，但是一開始，波茲曼認為兩者沒有區別。在這篇論文的後半段中，波茲曼還嘗試將原本只適用於理想氣體的馬克斯威爾分布推廣到一般的力學系統，他定義在相空間(phase space) 中的機率密度ρ(x)，古典力學中我們知道ρ沿著粒子的軌跡是不變的，稱之為Liouville 定理，假設系統總能量不變的話，在相空間上的曲面 H(x)=E (這裡的H是系統的漢密爾頓函數)上任一點都在某一條特定的軌跡上，那麼整個曲面的機率密度ρ都會相同，由此波茲曼寫出微正則系綜的機率密度ρ(x)，由此得到馬克斯威爾分布函數，所以現在我們通稱它為馬克斯威爾-波茲曼分布函數。這是第一次機率考量是應用在整個系統上，而不是單一個粒子。雖然這個推導比原先馬克斯威爾適用範圍要廣得多，卻必須仰賴一個嶄新的假設，就是遍歷性假設(ergodic hypothesis)。換句話說，對時間平均的而得的結果，與對系綜平均而得的結果"應該"是相同的。當時波茲曼還沒有理解到這樣的假設會有什麼問題。倒是他在1871年的論文提到過，當物體在相空間軌跡如果是封閉的，他的論證是不會成立的，因為曲面上就會有若干點不在同一條軌跡上，但是他認為一個至微小的擾動就會改變封閉的軌跡，所以這些封閉的軌跡的物理效應是可忽略的，這個議題可沒有這麼簡單就消失，我們在後面還會再提到它。

當然，敏銳的波茲曼知道之前的工作未臻完美，在一番努力之後，他在1872年發表了一篇非常重要的論文 Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen (Further studies on the thermal equilibrium of gas molecules)， 這篇論文之中，他提出兩項非常重要的東西，一樣是波茲曼方程式，另一樣則是所謂H定理。波茲曼再一次嘗試從微觀的動力學出發，希望能“證明”熱力學第二定律。所以他在提出波茲曼方程式來敘述了理想氣體系統內部粒子的運動情況。波爾茲曼方程式是一個非線性積微分方程式。方程式中的未知函數是一個包含了粒子空間位置和動量的六維機率密度函數f(r,p,t)。這個方程式描述粒子位置和動量機率分布如何在相空間中隨時間和空間變化，波茲曼的一個關鍵見解就是對碰撞項的確定。他假設的碰撞項完全是由假定在碰撞前不相關的兩個粒子的相互碰撞得到的。這個假設被波爾茲曼稱為「Stosszahlansatz」，其實正是馬克斯威爾之前所提的「分子混沌假設」。根據這一假設，碰撞項可以被寫作單粒子分布函數的乘積在動量空間上的積分。接下來他巧妙地定義了一個量H 是由f(E,t) (分子在時間t下的能量分布) 組成的一個奇特的積分:

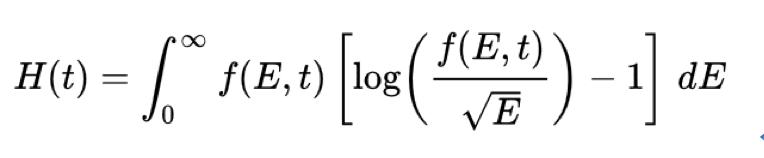
對於孤立理想氣體（總能量和分子數量不變），當f是馬克斯威爾-波茲曼分布時函數H會有極小值；如果系統處於其他分布時，H值會變大。波茲曼在這篇論文中證明，當波茲曼的碰撞項會使任何不是馬克斯威爾-波茲曼分布的f(E,t) 都不穩定，並且會發生不可逆的變化直到函數H達到最小值為止，換句話，f會朝向馬克士威-波茲曼分布演化! 在氣體容積不變的情況下，波茲曼發現他的函數H與克勞修斯定義的熵根本是同一回事，事實上熵等於−kH。波茲曼對這個結果非常自豪，他認為他已經用動力學證明了熱力學第二定律了！甚至他還認為他給出來的證明在數學上是站得住腳的嚴格證明。但背後是什麼機制造成的呢?

波茲曼的解釋是一個擁有龐大自由度的封閉系統會愈來愈混亂，愈來愈無序。而熵正是刻劃”無序”的物理量。波茲曼沿用馬克斯威爾的方法 氣體分子模型化為箱中相互碰撞的撞球，而隨著粒子間的碰撞，速度分布會變得愈來愈無序，最終導致了系統的巨觀性質趨於均勻，而微觀來看，則是系統處於最為無序的狀態，這是因為無序的微觀狀態數一定遠多於有序的微觀狀態數。如果讓系統自行演化，統計性地來看，系統到達微觀狀態數目多的機率也一定遠大於到達數目少機率。也就是說系統的熵一定會趨於最大值! 波茲曼總結道，粒子「以同樣的速率在同一方向」運動的有序狀態「可以想像，是系統最不可能處於的狀態，亦是最不可能的能量組態。」所以熱力學第二定律代表的是一個封閉系統不管起始狀態為何，最後都會趨向最為無序，也就是最為混亂的狀態!

更進一步，波茲曼在氣體運動論中發現了熵和微觀狀態的機率分布的對數關係， 並提出著名的波茲曼熵公式：

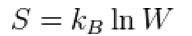
其中k = 1.3806505(24) × 10−23 J |K−1，稱作波茲曼常數。W是德語的機率（Wahrscheinlichkeit）的縮寫，這裡，更準確地說，W是系統的微觀狀態的數目。這個公式後來甚至刻在波茲曼的墓碑上，它為何如此重要呢? 因為正是這個看似簡單的公式提供了一個對大自然非常深刻的洞見。(不過第一個寫下這個公式的人並不是波茲曼，而是比他小十四歲的後輩，馬克斯‧普朗克在1900年寫書時第一次寫下來的!) 假設有N個粒子的理想氣體，Ni是粒子位置和動量的第i個微觀狀態。簡單的排列組合告訴我們：

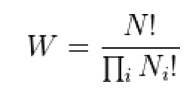
其中i的範圍是粒子所有可能的微觀狀態。

其實這個對熵的偉大洞見是源自於一場大辯論! 因為H定理中系統總是向H達到最小值的方向演化，然而顯然這違反了時間反演對稱，所謂時間反演對稱簡單地講就是將時間流向反過來如同錄影機倒帶一般。而微觀的古典力學卻總是遵循時間反演對稱的，所以當他昔日的恩師Johann Josef Loschmidt在1876年提出這個問題時，波茲曼陷入了苦戰。原先Loschmidt 是針對波茲曼將H定理推廣到系統在重力場中得到的結論而提出反駁，卻意外引發這一場"大戰"。

波茲曼很快就理解到，的確存在一些起始條件會讓H函數變大，但是波茲曼認為這些"例外"的起始條件只佔了可能的相空間中微不足道的一小部分，用波茲曼的說，H函數時間變大不是unmöglich(impossible) 而是unwahrscheinlich(improbable)。當然這並不能折服Loschmidt，所以波茲曼才會在1877年發表的Über die beziehung dem zweiten Haubtsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht (Concerning the relation of the second law of proposition of the mechanical theory of heat and the theory of probability respectively the theorems about the thermal equilibrium) 提出熵與微觀可能狀態數W的關聯，以此來為自己的理論辯護。1879年馬克斯威爾在病逝前發表了一篇On Boltzmann's Theorem on the Average Distribution of Energy in a System of Material Points 又重新燃起波茲曼對遍歷性假設的興趣，但是沒有太多新的進展。但是他在1884年給出了Stefan–Boltzmann law的證明又給了他信心，電磁學與熱力學第一次在他手上結合在一起，想必他一定相當自豪吧！

當然今天在基本粒子弱作用理論中時間反演對稱的確是被破壞的，但是如何從微觀系統微小的時間反演對稱破壞來解釋巨觀的時間反演對稱破壞卻仍然是一個困難的問題。另一角度來思考這個問題是以從宇宙論出發，換言之 如果邊界條件是違反時間反演對稱破壞(如大霹靂) 就算物理定律遵循時間反演對稱，我們還是會觀察到巨觀的時間反演對稱破壞。當然這是現代的觀點，與波茲曼時代的爭論關聯不大。

在Graz 的這段時間，波茲曼儼然已經成為德語世界新興的統計物理的一方之霸，為什麼最後他會走上悲劇的道路? 他的人生有會出現什麼波折? 這一些就留待下一回的阿文開講了。各位看官，Ate breve! Obrigado!

參考資料:

(一)中文 、英文 、德文維基相關條目

(二) Uffink, Jos, "Boltzmann's Work in Statistical Physics", The Stanford Encyclopedia of Philosophy (Spring 2017 Edition), Edward N. Zalta (ed.), URL = .

(三) "Josef Stefan: His life and legacy in the thermal sciences," Experimental Thermal and Fluid Science, Volume 31, Issue 7, July 2007,s 795–803, by John C. Crepeau

(四) Maxwell and the normal distribution: A colored story of probability, independence, and tendency toward equilibrium by Balázs Gyenis

(五) Lebowitz, J.L., (1999), “Statistical mechanics: A selective review of two central issues”, Reviews of Modern Physics, 71: S346-S357.

==================================================

延伸閱讀
為科學而生 為原子而死的波茲曼(下): 飄泊的靈魂