白努力定理的誤解與錯誤應用

在許多與流體相關的現象與物理演示中，最常被使用來解釋的定理就是白努力定理；常見的(演示)實例包含：「乒乓球的漂浮」、「變化球」、「紙片相吸」、及「飛機飛行」…但有許多的研究文獻已經指出這演示實例採用「白努力定理」的不當之處。這樣的錯誤說明充斥在教科書與許多網路資料中，連知名的科普雜誌（科學人2007年第67期9月號：伸卡球魔力何來？—變化球密技大解析）也不例外。透過「物理雙月刊」37卷三期(2015/06)國立彰化師範大學物理學系張慧貞教授「教科書對於演示實例之理解與誤解」一文，讓我們重新來了解「白努力定理」以及文獻上針對「白努力定理」誤用的探討。(以下內容節錄自「物理雙月刊」37卷三期國立彰化師範大學物理學系張慧貞教授所著「教科書對於演示實例之理解與誤解」一文）

「白努力定理」，常見的(演示)實例包含：「乒乓球的漂浮」(圖1)ㄛ、「變化球」(圖2)、「紙片相吸」(圖3)、及「飛機飛行」(圖4)…等。但透過理論與實驗的推證，多篇文獻指出這些演示實例採用「白努力定理」的不當之處。以「飛機飛行」為例，教科書中常見的敘述為：(1)因為機翼的上層距離較下層長，所以上層空氣的流速快、(2)根據「白努力」“流速快則壓力小”、(3)上下層之壓力差使飛機上升。
 

圖1：乒乓球的漂移


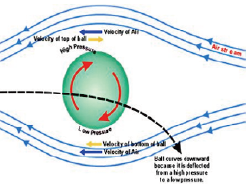
　圖2：變化球


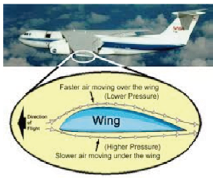
圖3：紙片相吸　 圖4：飛機飛行

文獻上有關白努力定理與飛機飛行的討論

然而，Babinsky (2003)反駁上述的解釋，首先，「白努力」的理論公式(P+ρgh+(1/2)ρυ²=常數)，是針對同一道流體的不同位置，根據「能量守恆」推導而得。所以相互比較速度(υ)與1壓力(P)的兩點，必須在同一道流體，而(1)機翼上、下層的氣流，已經不算同一道流體，故違反了白努力的限制條件。(2)根據實驗證據顯示，氣流通過機翼上下層後，並不會同時到達尾端(如圖5)，所以，「上層流速快」的推論也站不住腳。(3)「白努力」的公式僅顯示速度與壓力的大小關係，並未包含兩者之「因果」關係，若根據「牛頓定律」(ΣF=ma )的觀點，壓力的差異應該是速度變化的原因，而非結果(ΔP⟹ΣF⟹a⟹Δυ)，故正確的說法應是“壓力大則速度小”，而一般課本中則出現因果的倒置。
 

因此，「飛機飛行」並不符合「白努力」定理的範疇，同理類推其他三項演示，也都是針對不同流體做比較，違反「白努力」定理的限制。因此，無論是「乒乓球」、「變化球」、或「紙片相吸」的任何一種現象，都不能推論出「流速快空氣，壓力小於靜止的氣壓」的說法。

對此，Kamela(2007)也透過實驗證明，透過風吹空氣的壓力，不但沒有小於周邊靜止的氣壓，反而比較大。Babinsky (2003)也針對「紙片相吸」的演示提出質疑，因改為單張紙的一側吹氣，則並不會觀察到紙片向內彎曲的現象。因此，Kamela及Babinsky的兩篇文獻皆顯示，「流速大造成壓力小」的推論，在以上四項範例中皆不能成立，無論在理論或實驗的立場而言。

不是白努力定理？那是什麼呢？

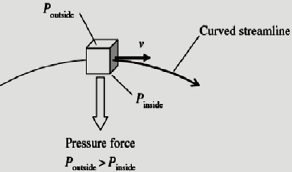
究竟這些現象該如何解釋呢？文獻也提出說明：Eastwell (2007) 認為此現象應使用「康達效應」(Coanda effect) 來解釋，又稱為「附璧效應」。Eastwell說“Th(e) tendency of a fluid to follow the shape of an obstacle, as a result of entrainment, is called Coanda effect. 意指: 流體遇到障礙物時(如機翼)，會有沿著障礙物曲面流動的傾向，因流線的彎曲需要向心力(向下，作用於流體)，而相對應的反作用力(向上，作用於機翼)，機翼便受到「提拉」(entrainment,或稱「挾持」或「拽引」)，使飛機上昇。Babinsky (2003)也認同Coanda effect才是關鍵的原因。並說明彎曲的流線，內外層氣壓會不均等(如圖6所示)，外層氣壓(向下)會大於內層(向上)，因此合力向下，提供流體彎曲所需的向心力。
 

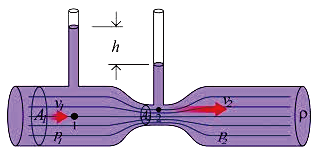
      讀者或許會問，既然大多數「白努力定理」的著名演示，皆不符合該原理的限制，那究竟有沒有符合「白努力」的實例呢？測量流速(如水的流速或風速)的「文丘里管」Venturi tube(如圖7所示)，就須採用「白努力」來解釋。因為在同一道流體上，截面積(A)的不同，造成流速(v)的不同(v∝1/A)，這是「連續方程」(Equation of Continuity)的概念；而根據「白努力」，流速的差異可以顯現出壓力差，看到流體上方的液面出現高度差。因此，「文丘里管」可利用h及A1、A2透過「白努力」，推算流速。

【參考資料】『觀念物理』：白努力定理的誤解與錯誤應用
Babinsky, H. (2003). How do wings work? Physics Education, 38(6), 497.
Kamela, M. (2007). Thinking about Bernoulli. The Physics Teacher, 45(6), 379-381.
Eastwell, P. H. (2007). Bernoulli? Perhaps, but what about viscosity. The Science Education Review, 6(1), 1-13.
同場加映：教科書對於演示實例之理解與誤解