音樂與物理的共舞
- 科學家隨筆
- 撰文者：駱俞衡 國立彰化師範大學 物理所物理教育組 碩士
- 發文日期：2020-09-26
- 點閱次數：9104
音樂是生活中的美好潤飾，咖啡廳裡撥放的輕柔古典樂、搭配歌詞傳達意涵的流行音樂、甚至是拿起一把吉他而隨意哼唱的創作，都為我們增添了不少樂趣。讀者是否想過，音階和物理的波動有哪些關係呢?相鄰音階(scale)的分割是否等間格呢?如何設計吉他指板上的寬度?本文將從古希臘時畢達哥拉斯(Pythagoras)以數學解析音階開始，接著以物理的角度解釋音階的訂定，進而探討吉他的設計。
音階
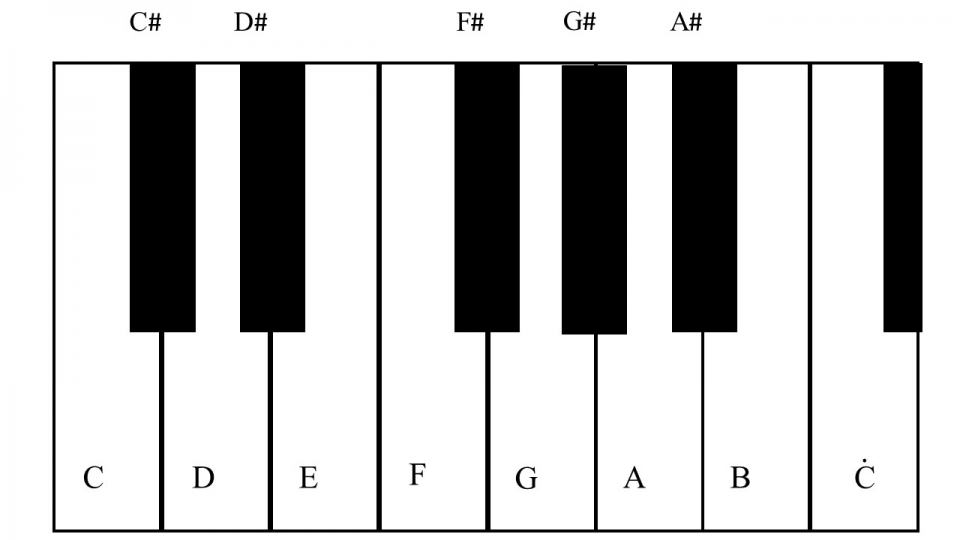
聲音三要素為響度、音調、及音色，對於音調的學習，在國中理化課告訴我們是由聲波的頻率決定；在初階音樂課則是唱著do、re、mi、fa、sol、la、si不同音高，並以固定唱名法對應音名C、D、E、F、G、A、B。而B繼續提升音高就以Ｃ表示，並再度循環音名使用，有如旋轉樓梯般循環向上，此Ｃ 至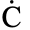
稱作高八度。再加入升(#)降(♭)音符，則共有12個不同的音高，稱作十二平均律(Equal Temperament) (圖一)。以鋼琴琴鍵觀察就可以明顯看見音高的排列，有升降記號的音為黑鍵，其餘則為白鍵(圖二)。
“十二平均律”中的”平均”一詞，容易讓人誤以為音與音之間為等差數列，即彼此間隔相等，但其實是為等比數列。不過，在討論“十二平均律”之前，必須先從古希臘時期畢達哥拉斯創建的“五度相生律”談起。
最初畢達哥拉斯在古希臘首創的八度音，將相鄰差兩倍的頻率定為八度音，例如:中央Ｃ 的頻率為261.6赫茲，那麼高八度的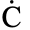
頻率就是 261.2*2=523.2 赫茲。接著，深信宇宙規則為簡單整數比的他，以C為準，將五度音差的G，訂為頻率比值為3/2倍，並將高四度的F，訂為頻率比4/3倍(如表一所示)。
其實，五度相生律一詞正說明了畢達哥拉斯創建音階的規則，也就是從C開始，每相差五度(頻率比值為3/2倍)，即生成下一個音，但若頻率超過兩倍時，代表已經跨到下一個八度音了，因此需再除以2。接著，我們就從音調C出發，以五度相生律推導音階：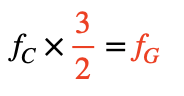
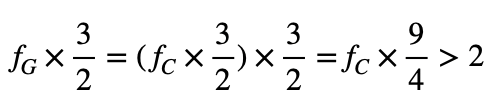
因為所乘頻率比值超過兩倍，所以除以2，得到
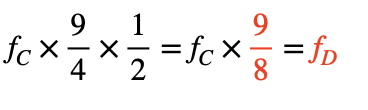
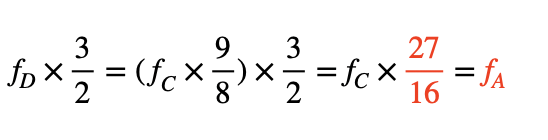
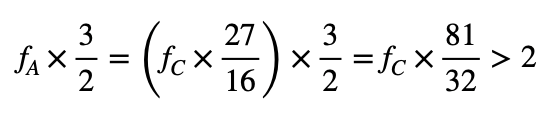
因為所乘頻率比值超過兩倍，所以除以2，得到
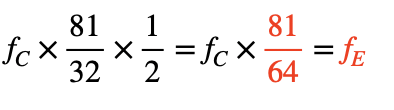
最後
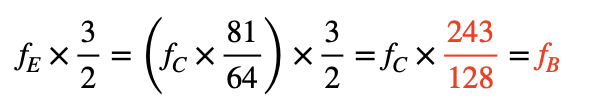
推至音調B時，我們已成功算出音調G、D、A、E、B之頻率，如圖三將推導過程化為圖示，可發現再加上原先之C及四度音F，就完成了以五度相生律構成之共7個音的音階了(如表一所示)。
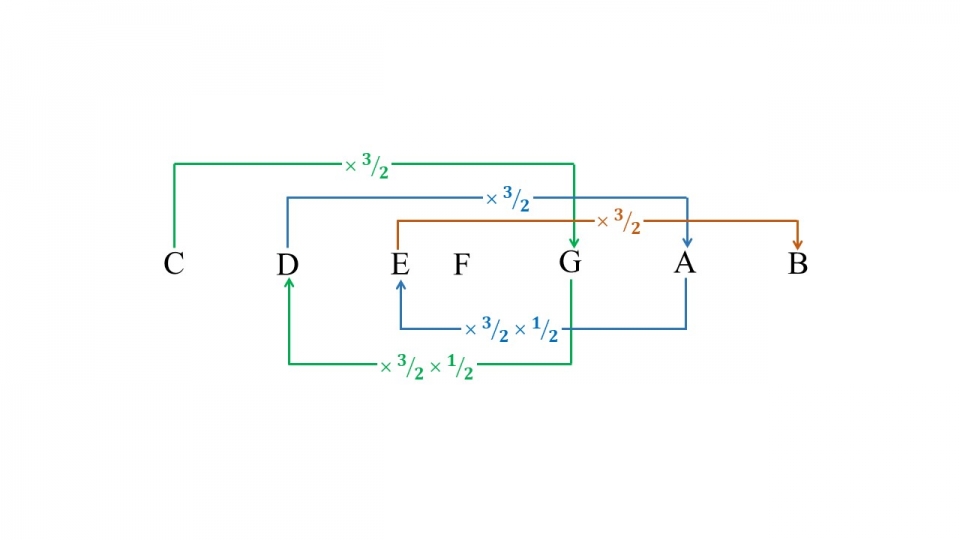
圖三、以五度相生律推算音階的過程
直到中國明代音樂家朱載堉於1584年，將共計12個音符，以相鄰音符之間成等比級數排列(而不是等差級數)，且承襲畢達哥拉斯制定八度音之間的頻率比值為兩倍，但刪除畢達哥拉斯原來定義的3/2倍五度音階制，而是將八度音間以等比級數分割為12個音符。所以相鄰音符間的頻率比值為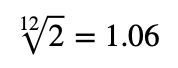
。例如:中央C頻率為 261.6赫茲，則C#頻率就是 261.6*1.06=277.2赫茲，D的頻率則為 261.6*1.062 =293.8 赫茲…，依此類推。就為我們現今最常使用的“十二平均律”。
駐波原理看不同樂器
最初的音樂型態來自大自然的聲響，包括鳥語啁啾、雨打樹葉、風吹青草等聲音，而後人們透過吼叫、敲打等等行為，漸漸發現能產生樂音。畢達哥拉斯(570B.C.-495 B.C.)就是聽見鐵匠敲打金屬時，發出了不同的聲音，而開啟了研究音樂的道路。逐漸發展至現今，我們早已有能力透過樂器自行創作與演奏音樂，更知道當初畢達哥拉斯聽見的不同聲音就是音調，也就是聲波的不同頻率。那樂器所發出的頻率，究竟由何決定？為什麼不同的樂器，仍有可能發出同一音調？
走進奇美博物館中的樂器廳，陳列了玲瑯滿目的樂器，若我們依樂器的頻率推導方式做分類，則可分為三種：兩端開管 (長笛、雙簧管等)、一端開管一端閉管(薩克斯風、單簧管等)和兩端皆固定的弦樂器(鋼琴、吉他等)。
管樂器的音調取決於震動空氣分子產生的駐波頻率。兩端開管樂器的駐波，頻率公式為
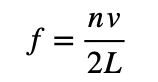
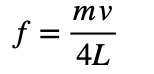
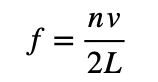
吉他的音樂與設計
♦吉他的弦與指板寬
接著，讓我們看向相當常見的弦樂器-吉他(如圖四)。
圖四
吉他的六根弦，有何差異呢? 粗細不同的弦，發出的聲音有甚麼差異呢?琴格的間距是否等間呢?如何讓同一根弦，發出不同音調的聲音呢?
以上問題，要從上述的駐波頻率開始講起。影響弦樂器基頻的因素：
且波速是由弦張力( F)和弦的線密度(µ )決定：
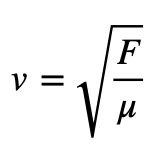
最後推出f 與L、µ、F的關係：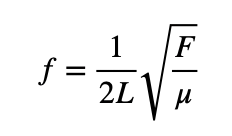 
若是同一根弦，則弦張力F和線密度 µ不變，基頻 f 和弦長L成反比，因此若要發出較高頻率的聲音，應將震動弦長L縮小，也就是將手指壓在遠離琴頭處。另外，也可以透過弦的粗細，也就是線密度(µ )，來調整頻率的大小。越細的弦，µ 越小，則頻率越大，所以越細的弦，音調越高。
同時，若仔細觀察吉他上琴格的寬度，不難發現其寬度是越來越窄。這是因為音階為等比數列，其頻率反比於弦長。所以弦長和音階一樣，為等比數列，兩相鄰音階的頻率比值為
。
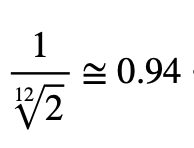實際推導吉他最粗的第六弦的弦長與頻率間之關係，並繪圖來推論。該弦的線密度µ=0.0074 kg/m，且不按壓指板直接彈奏第六弦時，需發出 E1的音調(f=82.4 Hz)，此時之弦長為0.646 公尺，因此可由
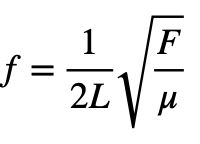
推導出弦的張力(F)應為83.8 N。接著，可根據音階的調升，推算出不同音符，所對應的弦長之數值關係(如表三)。
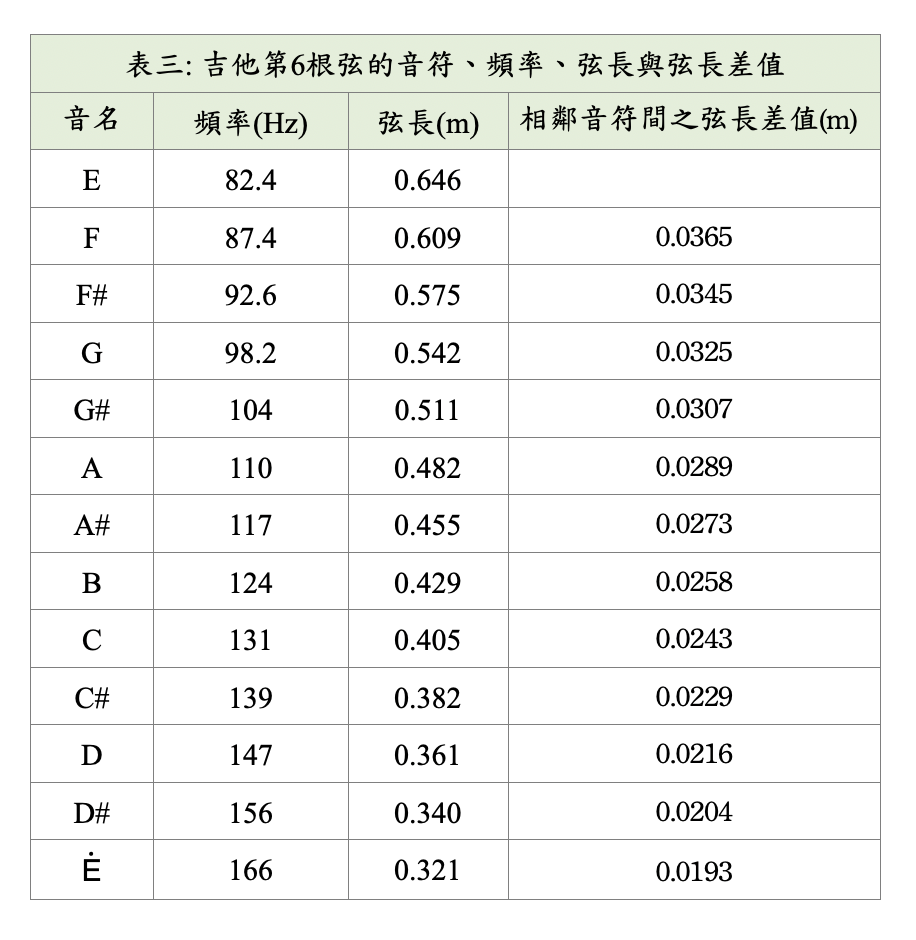
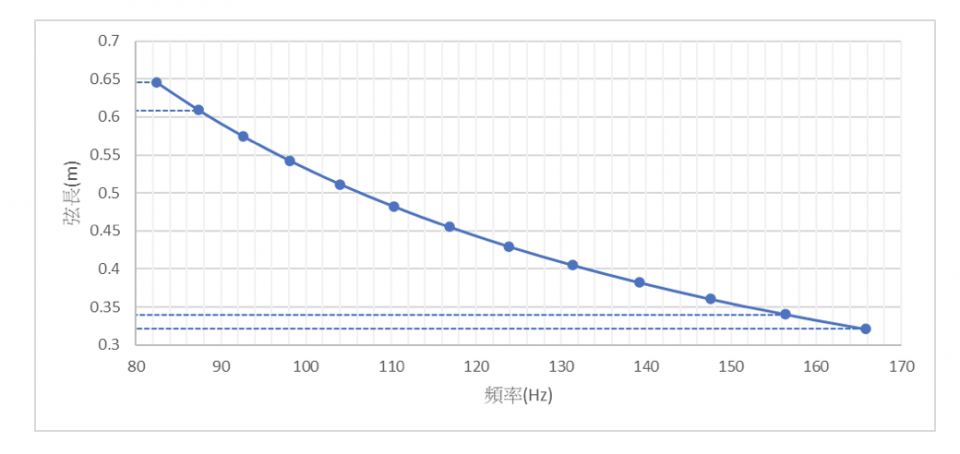
根據表三，可描繪出不同音符所對應的頻率及所需按壓的弦長(如圖五所示)。從圖五可看出，頻率越高對應的弦長越短，但並非為正比的斜直線，而是根號反比的曲線。同時，相臨音符的間距，隨著音調越高而越窄，音調最低的E至F，間距為3.65公分，而較高音的D#至 之間距，則縮短至1.93公分，可從圖六中的吉他指板上明顯觀察出此差異。
吉他為何需要六弦？
接著探討吉他為何需要六條弦?上述推導是吉他上最粗的第六弦，而線密度最小的第一弦，則可彈出更高的音調，因此，吉他整合六根粗細不同的弦，可彈奏出更廣的音域，且可巧妙地避免了同一弦彈奏至高音時，因為間距越來越小，而不易按準的問題。
不過，吉他的六根弦設計，原來不只為了顧及音域的寬廣，吉他的魅力之處，就是僅以一把吉他就可完整詮釋音樂的三要素-節奏、旋律及和聲。其中和聲需要用運不同音高的組合，並同時彈奏而形成和弦，例如: 同時彈出Do、Mi、So的和弦，需要三根弦。正是因為如此，若是一昧將六弦之間的音高差距增大，就難以彈奏出和弦了。
不只吉他，各式各樣的弦樂器也透過調整弦長、線密度及張力，巧妙地設計出該樂器彈奏所需的音越特性。例如:只有兩條弦的二胡，在國樂中需彈奏較高的音調，因此其弦的線密度相當於吉他的第一及第二弦。而不像吉他有著明顯的琴格供演奏者彈奏時的依據，隨著音調增高、弦長縮短，更考驗彈奏者的功力，才能確保彈奏出的音準。
綜合以上，我們可以看出，屬於理科的物理與數學，在屬於藝術的音樂發展歷程，扮演了重要的角色。將頻率等比級數排列而成音階，由此誕生了低至高的音符；由駐波頻率及波速之間的關係，不只了解弦樂器基頻和弦長、線密度及弦張力的關係，更由音階為等比級數排列的特性，掌握了吉他指板上相臨音符的間距，隨著音調越高而越窄。最後，更利用了線密度越小，則頻率越大的特性設計各式的弦樂器，使演奏者可輕易彈奏出和弦。
音樂為人們訴說故事與情感的一種工具，下次沉浸在音樂的同時，不妨也感受一下，藏匿在每個音符中的物理之美。
參考文獻
1. Inman, F. W. (2006). A standing-wave experiment with a guitar. The Physics Teacher, 44(7), 465-468.
2. LoPresto, M. C. (2006). Experimenting with guitar strings. The Physics Teacher, 44(8), 509-511.
3. Caleon, I., & Ramanathan, S. (2008). From music to physics: The undervalued legacy of Pythagoras. Science & Education, 17(4), 449-456.
4. Papadopoulos, A. (2002). Mathematics and music theory: From Pythagoras to Rameau. The Mathematical Intelligencer, 24(1), 65-73.
音階
聲音三要素為響度、音調、及音色，對於音調的學習，在國中理化課告訴我們是由聲波的頻率決定；在初階音樂課則是唱著do、re、mi、fa、sol、la、si不同音高，並以固定唱名法對應音名C、D、E、F、G、A、B。而B繼續提升音高就以Ｃ表示，並再度循環音名使用，有如旋轉樓梯般循環向上，此Ｃ 至
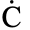稱作高八度。再加入升(#)降(♭)音符，則共有12個不同的音高，稱作十二平均律(Equal Temperament) (圖一)。以鋼琴琴鍵觀察就可以明顯看見音高的排列，有升降記號的音為黑鍵，其餘則為白鍵(圖二)。圖一、十二平均律(Equal Temperament)
圖二、鋼琴琴鍵與音階
音階排列：等差或等比？“十二平均律”中的”平均”一詞，容易讓人誤以為音與音之間為等差數列，即彼此間隔相等，但其實是為等比數列。不過，在討論“十二平均律”之前，必須先從古希臘時期畢達哥拉斯創建的“五度相生律”談起。
最初畢達哥拉斯在古希臘首創的八度音，將相鄰差兩倍的頻率定為八度音，例如:中央Ｃ 的頻率為261.6赫茲，那麼高八度的
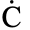
頻率就是 261.2*2=523.2 赫茲。接著，深信宇宙規則為簡單整數比的他，以C為準，將五度音差的G，訂為頻率比值為3/2倍，並將高四度的F，訂為頻率比4/3倍(如表一所示)。
其實，五度相生律一詞正說明了畢達哥拉斯創建音階的規則，也就是從C開始，每相差五度(頻率比值為3/2倍)，即生成下一個音，但若頻率超過兩倍時，代表已經跨到下一個八度音了，因此需再除以2。接著，我們就從音調C出發，以五度相生律推導音階：
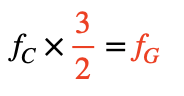
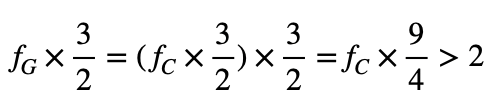
因為所乘頻率比值超過兩倍，所以除以2，得到
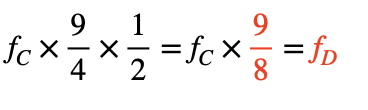
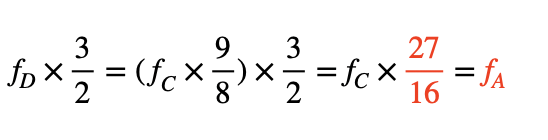
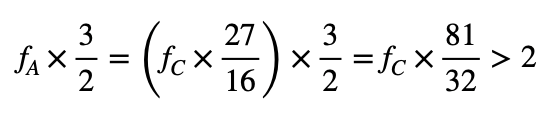
因為所乘頻率比值超過兩倍，所以除以2，得到
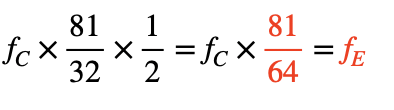
最後
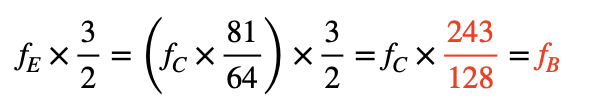
推至音調B時，我們已成功算出音調G、D、A、E、B之頻率，如圖三將推導過程化為圖示，可發現再加上原先之C及四度音F，就完成了以五度相生律構成之共7個音的音階了(如表一所示)。
圖三、以五度相生律推算音階的過程
之後的音樂學家為增加音調的精緻度，陸續以相同的方式增加音階的「成員」，也就是半音，八度音之中加入5個半音，加上原本的7個全音，共計12個音符。但不幸的是，若以五度相生的方式增加至12個音，會使音與音之間的頻率比值過於雜亂，導致某些合音，會產生不和諧的感覺。
直到中國明代音樂家朱載堉於1584年，將共計12個音符，以相鄰音符之間成等比級數排列(而不是等差級數)，且承襲畢達哥拉斯制定八度音之間的頻率比值為兩倍，但刪除畢達哥拉斯原來定義的3/2倍五度音階制，而是將八度音間以等比級數分割為12個音符。所以相鄰音符間的頻率比值為
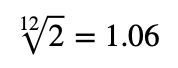。例如:中央C頻率為 261.6赫茲，則C#頻率就是 261.6*1.06=277.2赫茲，D的頻率則為 261.6*1.062 =293.8 赫茲…，依此類推。就為我們現今最常使用的“十二平均律”。駐波原理看不同樂器
最初的音樂型態來自大自然的聲響，包括鳥語啁啾、雨打樹葉、風吹青草等聲音，而後人們透過吼叫、敲打等等行為，漸漸發現能產生樂音。畢達哥拉斯(570B.C.-495 B.C.)就是聽見鐵匠敲打金屬時，發出了不同的聲音，而開啟了研究音樂的道路。逐漸發展至現今，我們早已有能力透過樂器自行創作與演奏音樂，更知道當初畢達哥拉斯聽見的不同聲音就是音調，也就是聲波的不同頻率。那樂器所發出的頻率，究竟由何決定？為什麼不同的樂器，仍有可能發出同一音調？
走進奇美博物館中的樂器廳，陳列了玲瑯滿目的樂器，若我們依樂器的頻率推導方式做分類，則可分為三種：兩端開管 (長笛、雙簧管等)、一端開管一端閉管(薩克斯風、單簧管等)和兩端皆固定的弦樂器(鋼琴、吉他等)。
管樂器的音調取決於震動空氣分子產生的駐波頻率。兩端開管樂器的駐波，頻率公式為
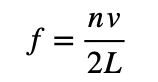
(L為樂器的管長、v為聲速，n為1、2、3…之正整數)，其中，聲速主要受空氣溫度的影響，即 ( T為溫度，單位為攝氏)，當n=1時的頻率稱之基頻，而基頻決定了音高，其餘 稱之泛音，泛音決定其音色。第二種樂器為，一端開管一端閉管的管樂器，其駐波頻率為
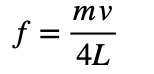
(L為樂器的管長、v為聲速，m為1、3、5…之奇數)，相同的，m=1時的頻率稱之基頻，其餘 等等的頻率皆為泛音。
最後，弦樂器的駐波頻率為
最後，弦樂器的駐波頻率為
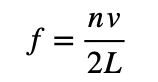
(L為樂器的管長、v為聲速，n為1、2、3…之整數)，和兩端開管樂器的駐波頻率公式恰好相同。但因弦樂器為透過弦的震動產生聲音，因此其波速主要受到弦的張力及線密度控制，即
(F為弦張力， 為線密度)。因此，弦樂器的音調與空氣的溫度無關，而管樂器則與氣溫有關。
總結以上不同樂器與音高(基頻)間的關係為表二：
(F為弦張力， 為線密度)。因此，弦樂器的音調與空氣的溫度無關，而管樂器則與氣溫有關。
總結以上不同樂器與音高(基頻)間的關係為表二：
表二：不同樂器與音高(基頻)間的關係
吉他的音樂與設計
♦吉他的弦與指板寬
接著，讓我們看向相當常見的弦樂器-吉他(如圖四)。
圖四
吉他的六根弦，有何差異呢? 粗細不同的弦，發出的聲音有甚麼差異呢?琴格的間距是否等間呢?如何讓同一根弦，發出不同音調的聲音呢?
以上問題，要從上述的駐波頻率開始講起。影響弦樂器基頻的因素：
弦樂器基頻：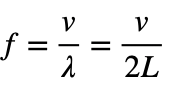 
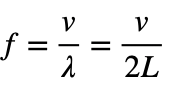
且波速是由弦張力( F)和弦的線密度(µ )決定：
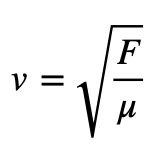
最後推出f 與L、µ、F的關係：
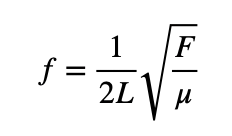
若是同一根弦，則弦張力F和線密度 µ不變，基頻 f 和弦長L成反比，因此若要發出較高頻率的聲音，應將震動弦長L縮小，也就是將手指壓在遠離琴頭處。另外，也可以透過弦的粗細，也就是線密度(µ )，來調整頻率的大小。越細的弦，µ 越小，則頻率越大，所以越細的弦，音調越高。
同時，若仔細觀察吉他上琴格的寬度，不難發現其寬度是越來越窄。這是因為音階為等比數列，其頻率反比於弦長。所以弦長和音階一樣，為等比數列，兩相鄰音階的頻率比值為
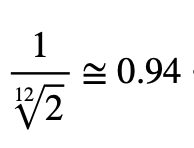。實際推導吉他最粗的第六弦的弦長與頻率間之關係，並繪圖來推論。該弦的線密度µ=0.0074 kg/m，且不按壓指板直接彈奏第六弦時，需發出 E1的音調(f=82.4 Hz)，此時之弦長為0.646 公尺，因此可由
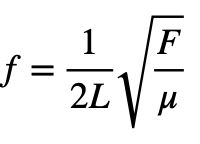
推導出弦的張力(F)應為83.8 N。接著，可根據音階的調升，推算出不同音符，所對應的弦長之數值關係(如表三)。
根據表三，可描繪出不同音符所對應的頻率及所需按壓的弦長(如圖五所示)。從圖五可看出，頻率越高對應的弦長越短，但並非為正比的斜直線，而是根號反比的曲線。同時，相臨音符的間距，隨著音調越高而越窄，音調最低的E至F，間距為3.65公分，而較高音的D#至 之間距，則縮短至1.93公分，可從圖六中的吉他指板上明顯觀察出此差異。
表三: 吉他第6根弦的音符、頻率、弦長與弦長差值
圖五、吉他第六根弦的弦長與頻率之關係
圖六、吉他指板間距比較
吉他為何需要六弦？
接著探討吉他為何需要六條弦?上述推導是吉他上最粗的第六弦，而線密度最小的第一弦，則可彈出更高的音調，因此，吉他整合六根粗細不同的弦，可彈奏出更廣的音域，且可巧妙地避免了同一弦彈奏至高音時，因為間距越來越小，而不易按準的問題。
不過，吉他的六根弦設計，原來不只為了顧及音域的寬廣，吉他的魅力之處，就是僅以一把吉他就可完整詮釋音樂的三要素-節奏、旋律及和聲。其中和聲需要用運不同音高的組合，並同時彈奏而形成和弦，例如: 同時彈出Do、Mi、So的和弦，需要三根弦。正是因為如此，若是一昧將六弦之間的音高差距增大，就難以彈奏出和弦了。
不只吉他，各式各樣的弦樂器也透過調整弦長、線密度及張力，巧妙地設計出該樂器彈奏所需的音越特性。例如:只有兩條弦的二胡，在國樂中需彈奏較高的音調，因此其弦的線密度相當於吉他的第一及第二弦。而不像吉他有著明顯的琴格供演奏者彈奏時的依據，隨著音調增高、弦長縮短，更考驗彈奏者的功力，才能確保彈奏出的音準。
綜合以上，我們可以看出，屬於理科的物理與數學，在屬於藝術的音樂發展歷程，扮演了重要的角色。將頻率等比級數排列而成音階，由此誕生了低至高的音符；由駐波頻率及波速之間的關係，不只了解弦樂器基頻和弦長、線密度及弦張力的關係，更由音階為等比級數排列的特性，掌握了吉他指板上相臨音符的間距，隨著音調越高而越窄。最後，更利用了線密度越小，則頻率越大的特性設計各式的弦樂器，使演奏者可輕易彈奏出和弦。
音樂為人們訴說故事與情感的一種工具，下次沉浸在音樂的同時，不妨也感受一下，藏匿在每個音符中的物理之美。
參考文獻
1. Inman, F. W. (2006). A standing-wave experiment with a guitar. The Physics Teacher, 44(7), 465-468.
2. LoPresto, M. C. (2006). Experimenting with guitar strings. The Physics Teacher, 44(8), 509-511.
3. Caleon, I., & Ramanathan, S. (2008). From music to physics: The undervalued legacy of Pythagoras. Science & Education, 17(4), 449-456.
4. Papadopoulos, A. (2002). Mathematics and music theory: From Pythagoras to Rameau. The Mathematical Intelligencer, 24(1), 65-73.