
粒子物理行(九)反物質
- 粒子物理行
- 撰文者:黎偉健
- 發文日期:2020-07-31
- 點閱次數:2622
在前幾章,我們認識到粒子物理的基本概念和四種基本交互作用。由本章開始,我們會探討粒子物理的一些具體的有趣現象。這些現象違反直觀,甚至荒誕離奇,但都一一被實驗證實。在本章,我們會介紹量子場論的一個驚人結論-----反物質。
反粒子
在第二章,我們知道粒子的種類由它的質量m、自旋s和荷n標籖。質量和自旋是守恆的時空物理量,源於連續時空對稱;荷是守恆的內在物理量,源於內在對稱【註1】。荷的最簡單例子是電荷,它決定了粒子與光子交互作用的性質。電荷是一個實數,可正可負。例如,電子帶負電荷,而質子帶正電荷。荷的另一例子是色荷,它決定了粒子於膠子交互作用的性質。夸克和膠子都帶色荷(詳述見第七章)。量子場論有以下重要定理:
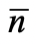 的粒子,稱為X的反粒子,記為
的粒子,稱為X的反粒子,記為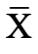 。
。所以,存在一種粒子,它的質量和自旋與電子相等 ( m=0.511 MeV,s=1/2 ),但電荷是電子電荷的相反值。這粒子稱為電子的反粒子,又稱為反電子或正電子,記為 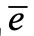 或
或 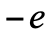 。電子的電荷為 (
。電子的電荷為 ( 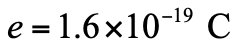 ),而正電子的電荷為
),而正電子的電荷為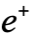 。類似地,質子也有其反粒子,稱為反質子,其質量和自旋與質子相等 ( m=938 MeV,s=1/2 ),但電荷為質子電荷的相反值,即為
。類似地,質子也有其反粒子,稱為反質子,其質量和自旋與質子相等 ( m=938 MeV,s=1/2 ),但電荷為質子電荷的相反值,即為 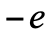 。所以,電子和正電子之間存在靜電吸引力,甚至可以互相圍繞運動,組成複合粒子,稱為正電子素 (positronium)。正電子和反質子之間也存在靜電吸引力,也會組成複合粒子。該複合粒子是氫原子的反粒子,也就是反氫原子。那麼中子呢?中子不帶電荷,也不帶色荷(一切在實驗探測到的粒子均不帶色荷),那麼中子有其反粒子嗎?注意,中子由三顆夸克組成,夸克成份是udd(u為上夸克,d為下夸克)。我們在第八章中知道,夸克帶弱同位旋。u帶弱同位上旋,d帶弱同位下旋,所以組合udd帶弱同位下旋【註2】,因此中子帶弱同位下旋。所以,中子有其反粒子,夸克成份為
。所以,電子和正電子之間存在靜電吸引力,甚至可以互相圍繞運動,組成複合粒子,稱為正電子素 (positronium)。正電子和反質子之間也存在靜電吸引力,也會組成複合粒子。該複合粒子是氫原子的反粒子,也就是反氫原子。那麼中子呢?中子不帶電荷,也不帶色荷(一切在實驗探測到的粒子均不帶色荷),那麼中子有其反粒子嗎?注意,中子由三顆夸克組成,夸克成份是udd(u為上夸克,d為下夸克)。我們在第八章中知道,夸克帶弱同位旋。u帶弱同位上旋,d帶弱同位下旋,所以組合udd帶弱同位下旋【註2】,因此中子帶弱同位下旋。所以,中子有其反粒子,夸克成份為 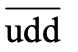 (其中
(其中 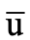 和
和 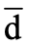 分別為u和d的反粒子【註3】),其質量和自旋與中子相等 ( m=940 MeV,s=1/2 ),不帶電荷和色荷,但帶弱同位上旋(與中子的弱同位下旋相反)。類似反氫原子,一切化學原素的原子皆有其反原子,它們由反電子、反質子和反中子組成。我們日常接觸到的世界都由原子組成,而每個原子都有與其對應的反原子。那麼,我們可以想像一個反世界,該世界的組成彷彿是把我們世界的每顆原子換成反原子。在這個由反物質組成的反世界裏,有反地球、反月球、反太陽。反地球上有反生物:反植物、反人類、反貓、反狗。問題是,既然由反物質組成的星體有可能存在,為什麼我們從没發現過它?換句話說,既然粒子和反粒子所帶的荷恰好相反,並且時空性質(如質量和自旋)相同,正反物質理應完全對稱,為何這個世界只由物質組成,而不由反物質組成?這是一個未解決的物理學難題,它涉及到物理定律的基礎對稱性和宇宙的早期演化史。在探討這個問題之前,讓我們先了解正反粒子之間的對稱性-----電荷共軛對稱。
分別為u和d的反粒子【註3】),其質量和自旋與中子相等 ( m=940 MeV,s=1/2 ),不帶電荷和色荷,但帶弱同位上旋(與中子的弱同位下旋相反)。類似反氫原子,一切化學原素的原子皆有其反原子,它們由反電子、反質子和反中子組成。我們日常接觸到的世界都由原子組成,而每個原子都有與其對應的反原子。那麼,我們可以想像一個反世界,該世界的組成彷彿是把我們世界的每顆原子換成反原子。在這個由反物質組成的反世界裏,有反地球、反月球、反太陽。反地球上有反生物:反植物、反人類、反貓、反狗。問題是,既然由反物質組成的星體有可能存在,為什麼我們從没發現過它?換句話說,既然粒子和反粒子所帶的荷恰好相反,並且時空性質(如質量和自旋)相同,正反物質理應完全對稱,為何這個世界只由物質組成,而不由反物質組成?這是一個未解決的物理學難題,它涉及到物理定律的基礎對稱性和宇宙的早期演化史。在探討這個問題之前,讓我們先了解正反粒子之間的對稱性-----電荷共軛對稱。
電荷共軛對稱
讓我們先想想一個有趣的問題:我們憑什麼說組成這個世界的不是反物質。試想想,如果電子的電荷為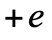 ,質子的電荷為
,質子的電荷為 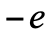 ,它們互相吸引,組成原子,這與電子電荷為
,它們互相吸引,組成原子,這與電子電荷為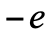 並且質子電荷為
並且質子電荷為 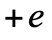 的情形完全没有分別。也就是說,物理定律在正反粒子變換
的情形完全没有分別。也就是說,物理定律在正反粒子變換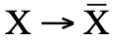 下不變,這種對稱性稱為電荷共軛對稱 (charge conjugation symmetry),而變換
下不變,這種對稱性稱為電荷共軛對稱 (charge conjugation symmetry),而變換 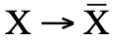 稱為電荷共軛變換。電荷共軛變換把粒子帶的所有荷變成相反,而保持動量、能量、質量和角動量等時空物理量不變。 電荷共軛變換可以看成內在空間的宇稱變換(即把內在空間的向量方向反轉)。反粒子其實就是粒子在內在空間中的鏡像。
稱為電荷共軛變換。電荷共軛變換把粒子帶的所有荷變成相反,而保持動量、能量、質量和角動量等時空物理量不變。 電荷共軛變換可以看成內在空間的宇稱變換(即把內在空間的向量方向反轉)。反粒子其實就是粒子在內在空間中的鏡像。
在第二章,我們知道,一顆自由粒子的態記為
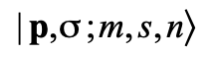
其中p為動量, 為螺旋度 (helicity),m為質量,s為自旋,n為荷。電荷共軛變換C是一個算子,它作用在粒子態時給出對應的反粒子的態:
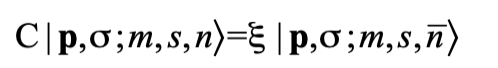
其中 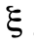 是一個模長為1的複數,稱為電荷共軛宇稱 (charge conjugation parity)。對於已知粒子,
是一個模長為1的複數,稱為電荷共軛宇稱 (charge conjugation parity)。對於已知粒子,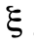 取值1或-1。
取值1或-1。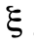 取決於粒子種類。例如,對於質子、中子和電子,
取決於粒子種類。例如,對於質子、中子和電子,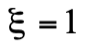 (或者我們會直接說對於質子、中子和電子,C=1 )。
(或者我們會直接說對於質子、中子和電子,C=1 )。
C是一個乘法量子數 (multiplicative quantum number),即多粒子態的 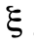 是單粒子態的
是單粒子態的 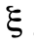 的乘積。例如,考慮一個有兩顆電子的雙粒子態
的乘積。例如,考慮一個有兩顆電子的雙粒子態
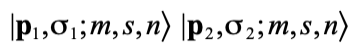
它在C的作用下變換成一個有兩顆正電子的態,並且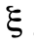 為電子的
為電子的 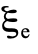 的積,即
的積,即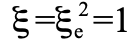 :
:
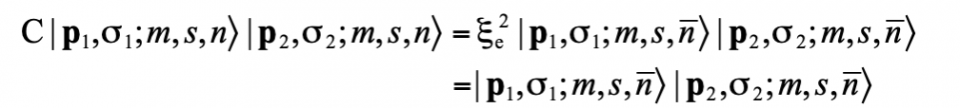
對於某些粒子,由於它們不帶荷,又或者反荷與荷相同,它們的反粒子與自身無異,即它們是自身的反粒子。例如,光子不帶荷,所以是自身的反粒子。又例如膠子,它帶伴隨色荷 (adjoint color charge),即同時帶有基本色荷和反基本色荷,所以也是自身的反粒子。對於是自身的反粒子的粒子,C對粒子態的作用為
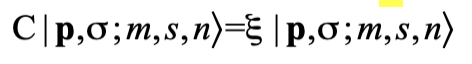
也就是說,粒子態為C的本徵態,本徵值為 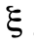 。例如,對於光子(記為
。例如,對於光子(記為 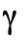 ),
),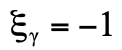 。
。
根據第二章介紹到的諾特定理,電荷共軛對稱作為一種對稱性,對應一守恆量,而這守恆量便是C。即是說,如果物理定律遵從電荷共軛對稱,那麼對於任何物理過程,如果初態是C的本徵態,本徵值為 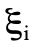 ,則終態也是C的本徵態,本徵值
,則終態也是C的本徵態,本徵值 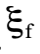 與
與 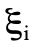 相等,即
相等,即 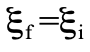 。根據粒子物理的標準模型和廣義相對論,電磁交互作用、強交互作用和重力交互作用嚴格遵守電荷共軛對稱,即C守恆。例如,我們從實驗得知,中性
。根據粒子物理的標準模型和廣義相對論,電磁交互作用、強交互作用和重力交互作用嚴格遵守電荷共軛對稱,即C守恆。例如,我們從實驗得知,中性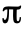 介子
介子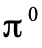 會衰變成兩顆光子 (
會衰變成兩顆光子 ( 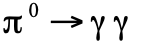 )。由於該過程涉及到光子的產生,所以是電磁交互作用的結果,因此C守恆。終態是兩顆光子,其
)。由於該過程涉及到光子的產生,所以是電磁交互作用的結果,因此C守恆。終態是兩顆光子,其 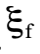 為
為 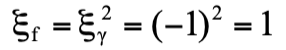 ,所以初態的
,所以初態的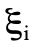 為1,即
為1,即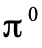 的
的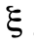 為1(即
為1(即 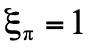 )。那麼,由於三顆光子的態的
)。那麼,由於三顆光子的態的 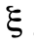 是
是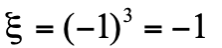 ,
,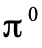 不可能衰變成三顆光子。事實上,衰變
不可能衰變成三顆光子。事實上,衰變  從沒有在實驗被發現過。又例如,考慮兩顆光子的散射 γγ→nγ,其終態是n顆光子。初態的
從沒有在實驗被發現過。又例如,考慮兩顆光子的散射 γγ→nγ,其終態是n顆光子。初態的 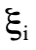 為
為 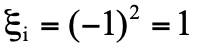 ,而終態的
,而終態的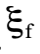 為
為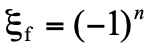 。由於該散射過程涉及光子間的交互作用,所以也是電磁交互作用的結果,因此C守恆。由
。由於該散射過程涉及光子間的交互作用,所以也是電磁交互作用的結果,因此C守恆。由 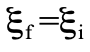 ,我們得知(-1)n=1 ,即n為雙數。所以,散射過程如 γγ→3γ 或 γγ→5γ ,終態涉及單數顆光子,違反C守恆,不會發生。
,我們得知(-1)n=1 ,即n為雙數。所以,散射過程如 γγ→3γ 或 γγ→5γ ,終態涉及單數顆光子,違反C守恆,不會發生。
湮滅作用
考慮散射過程 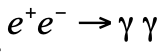 ,其中一顆電子和一顆正電子相撞,變成兩顆光子。這是一種非彈性散射 (inelastic scattering),即終態的粒子與初態的粒子種類不同。我們稱這種正反粒子相遇而變成其他粒子的過程為湮滅作用 (annihilation)。湮滅作用在粒子加速器實驗裏十分常見,尤其是電子-正電子和正反質子的湮滅作用。電子-正電子湮滅作用的費曼圖如圖一,其中左端是初態,右端是終態,直線代表電子或正電子,波浪線代表光子。直線上的箭頭方向是電子電荷的流動方向,即若該箭頭指向右方(順時方向),該線在代表電子的運動;若該箭頭指向左方(逆時方向),該線在代表正電子的運動。我們也可考慮圖一的時間反演,如圖二,即兩顆光子互相湮滅,變成一顆電子和一顆正電子 (
,其中一顆電子和一顆正電子相撞,變成兩顆光子。這是一種非彈性散射 (inelastic scattering),即終態的粒子與初態的粒子種類不同。我們稱這種正反粒子相遇而變成其他粒子的過程為湮滅作用 (annihilation)。湮滅作用在粒子加速器實驗裏十分常見,尤其是電子-正電子和正反質子的湮滅作用。電子-正電子湮滅作用的費曼圖如圖一,其中左端是初態,右端是終態,直線代表電子或正電子,波浪線代表光子。直線上的箭頭方向是電子電荷的流動方向,即若該箭頭指向右方(順時方向),該線在代表電子的運動;若該箭頭指向左方(逆時方向),該線在代表正電子的運動。我們也可考慮圖一的時間反演,如圖二,即兩顆光子互相湮滅,變成一顆電子和一顆正電子 ( 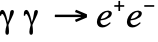 )。當然,由於能量守恆,要過程
)。當然,由於能量守恆,要過程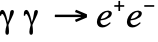 發生,初態總能量必須最小為終態粒子質量的和,即電子質量的兩倍,即約 1 MeV 。
發生,初態總能量必須最小為終態粒子質量的和,即電子質量的兩倍,即約 1 MeV 。
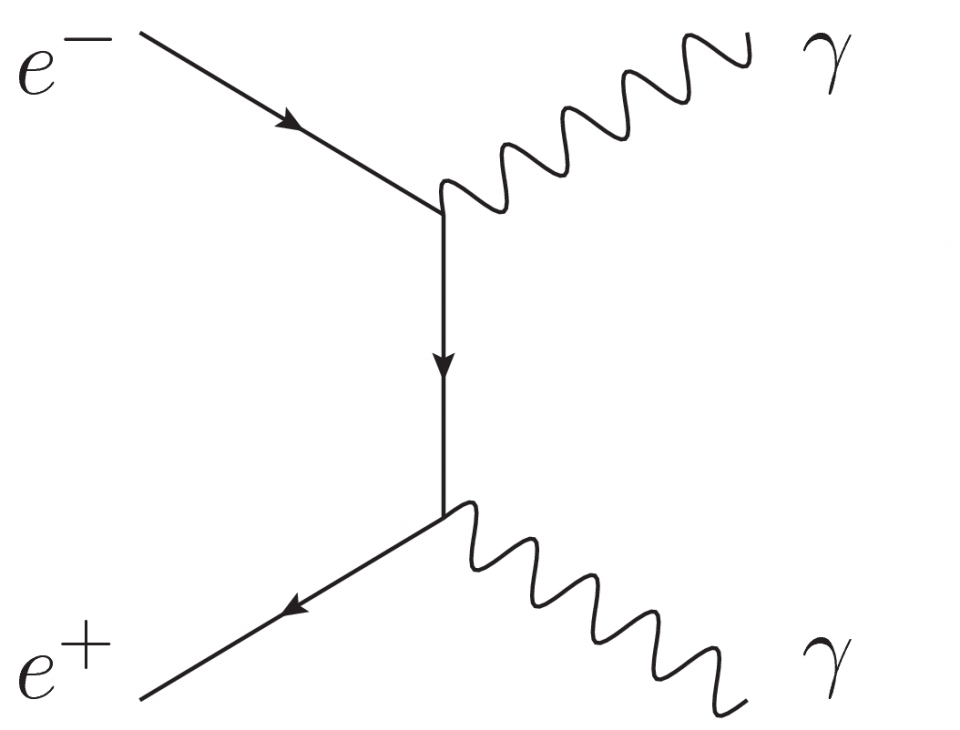
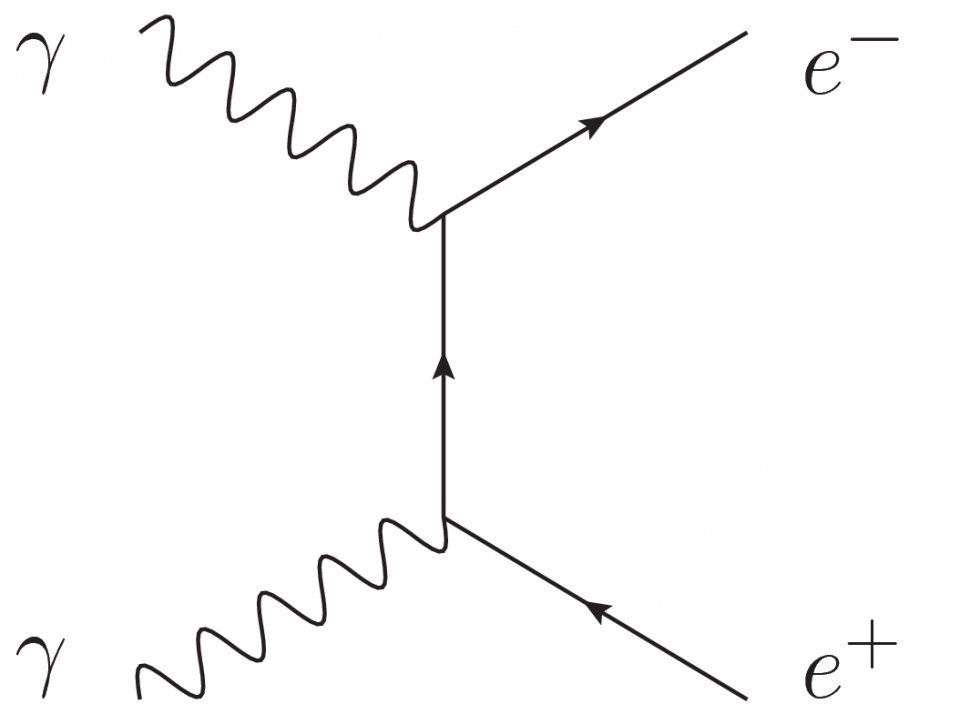
圖一 圖二
正反物質不對稱
回到我們當初問的問題:為何這個世界只由物質組成,而不由反物質組成?從以上討論,我們知道,當物質遇上反物質,它們有可能互相湮滅,變成光子。即使一顆電子和一顆正電子互相圍繞,組成正電子素,它們也有可能因量子力學中的位置不確定性而相遇,並且互相湮滅,所以正電子素會衰變成光子。注意,正反粒子的湮滅只會使粒子的數量和反粒子的數量作相同分量減少,而兩數量的差保持不變。跟據宇宙學的標準模型,宇宙的誕生源於大爆炸。假設在宇宙的初始態中,每種粒子的正反粒子數量相同。那麼,如果物理定律嚴格遵守電荷共軛對稱,宇宙中於任一時刻的正反粒子數量理應相同,所以物質不可能多於反物質。可是,如果物理定律並不嚴格遵守電荷共軛對稱,物質與反物質數量便可能不同。在粒子物理的標準模型裏,弱交互作用並不遵從電荷共軛對稱。可是,弱交互作用對電荷共軛對稱的違反並不足以解釋宇宙中正反物質數量不對稱的的大小。
根據我們現在對宇宙演化史的認識,我們還未能對正反物質數量不對稱作完滿解釋。更有趣的是 ,根據觀測,設宇宙重子(如質子和中子)的平均數量密度為 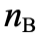 ,光子平均數量密度為
,光子平均數量密度為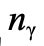 ,那麼
,那麼 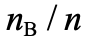 的數量級約為10-9,即重子數量遠少於光子數量。根據大爆炸理論,宇宙初期溫度極高,如圖一和圖二(其中直線可以是重子或電子)的煙滅作用頻繁發生,這使重子、反重子、電子、反電子和光子的數量相約。隨着宇宙膨漲,溫度下降,粒子平均能量也會下降。當光子的平均能量遠小於重子和電子的質量,由於能量守恆,圖二的光子煙滅過程便不可能發生,而圖一的重子或電子的煙滅過程仍然能發生。也就是說,隨着宇宙的溫度下降,大量正反物質會互相湮減,轉化成光子。這些光子便是我們今天能觀察到的宇宙微波背景輻射 (cosmic microwave background)。剩下沒有湮滅的正物質(如質子、中子和電子),數量僅為光子數量的十億份之一,組成了宇宙中各種天體,如恆星和行星。所以,我們現今所見到的天體,都是宇宙初期大規模正反物質煙滅作用的小量殘留物。由此,我們可以推斷,設
的數量級約為10-9,即重子數量遠少於光子數量。根據大爆炸理論,宇宙初期溫度極高,如圖一和圖二(其中直線可以是重子或電子)的煙滅作用頻繁發生,這使重子、反重子、電子、反電子和光子的數量相約。隨着宇宙膨漲,溫度下降,粒子平均能量也會下降。當光子的平均能量遠小於重子和電子的質量,由於能量守恆,圖二的光子煙滅過程便不可能發生,而圖一的重子或電子的煙滅過程仍然能發生。也就是說,隨着宇宙的溫度下降,大量正反物質會互相湮減,轉化成光子。這些光子便是我們今天能觀察到的宇宙微波背景輻射 (cosmic microwave background)。剩下沒有湮滅的正物質(如質子、中子和電子),數量僅為光子數量的十億份之一,組成了宇宙中各種天體,如恆星和行星。所以,我們現今所見到的天體,都是宇宙初期大規模正反物質煙滅作用的小量殘留物。由此,我們可以推斷,設 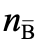 為反重子的平均數量密度,那麼對於宇宙初期,
為反重子的平均數量密度,那麼對於宇宙初期,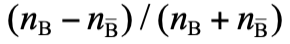 的數量級約為10-9,即正反粒子數量的差僅為正反粒子數量總和的十億份之一。解釋宇宙早期裏正反粒子數量的這個極微小差距是當代粒子物理學的一門重要課題。
的數量級約為10-9,即正反粒子數量的差僅為正反粒子數量總和的十億份之一。解釋宇宙早期裏正反粒子數量的這個極微小差距是當代粒子物理學的一門重要課題。
一些歷史
反粒子的發現史是科學史上輝煌的一章。非相對論性量子力學於1925至1926年被海森堡 (Heisenberg)、玻恩 (Born)、約當 (P. Jordan)、狄拉克 (Dirac) 和薜丁格 (Schrödinger) 等人創立。當時很多物理學家都致力尋求一套能結合量子力學和狹義相對論的理論體系。薜丁格在發表薜丁格方程式之前,已經發現了一條相對論性的波動方程式。但由於該方程給出的氫原子光譜的精細結構與實驗不符,薜丁格並沒有在他於1926年發表的波動力學論文中使用。此方程式於同年被其他數位物理學家獨立發現,現在稱為Klein-Gordon方程式。現在我們知道,該方程式之所以不能準確描述氫原子光譜,是因為它描述的是自旋為零的粒子,而電子的自旋為1/2。狄拉克對Klein-Gordon方程式感到不滿,但並不是基於其描述粒子的自旋為零,而是因為該方程式所蘊含的守恆量不必為正數,因此不可能代表概率,與量子力學不符。從現代的觀點看,狄拉克的憂慮是不必的,因為Klein-Gordon的守恆量是電荷,而不是概率,而電荷取值可正可負。
1927年,包立 (Pauli) 發現了描述自旋角動量為 s=1/2 的數學理論。狄拉克基於對方程式中守恆量的正定性、對自旋的考慮、以及狹義相對論的協變性,於1928年提出了以下方程式:
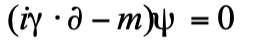
此方程式稱為狄拉克方程式。在此,我們不須深究方程式中符號的具體意義,只須知道 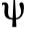 具有四個分量。給定確定的動量,該方程式有四個解:兩個解具有正能量,兩個解具有負能量。正能量的兩個解分別對應上旋和下旋粒子,恰如電子。在加入與電磁場的耦合後,狄拉克方程式給出了正確的電子磁偶極矩,並準確描述了氫原子的光譜,包括其精細結構。並且,狄拉克方程式的守恆量最正值,可視為粒子出現的概率。這些空前的成功,使當時的物理家都認為狄拉克方程式就是描述電子的正確方程式。
具有四個分量。給定確定的動量,該方程式有四個解:兩個解具有正能量,兩個解具有負能量。正能量的兩個解分別對應上旋和下旋粒子,恰如電子。在加入與電磁場的耦合後,狄拉克方程式給出了正確的電子磁偶極矩,並準確描述了氫原子的光譜,包括其精細結構。並且,狄拉克方程式的守恆量最正值,可視為粒子出現的概率。這些空前的成功,使當時的物理家都認為狄拉克方程式就是描述電子的正確方程式。
可是,那兩個負能量解究竟代表甚麼?狄拉克起初對此並沒有答案。狄拉克只知道,負能量解的電荷與正能量解的電荷恰好相反,並且質量相等。當時,物理學家所知的「基本粒子」只有三顆:質子、電子和光子。外爾 (Weyl) 於1929年提出,負能量解對應質子。狄拉克反駁,因為電子衰變成負能量解(質子)的過程會違反電荷守恆。為解決這矛盾,狄拉克提出負能量解是真空的激發,稱為洞 (hole),並暫定洞為質子。1930年,奧本海墨 (Oppenheimer) 指出如果狄拉克的洞理論正確,並且洞是質子,那麼質子和電子會互相湮滅成光子,即氫原子會衰變成光子,半衰期約為10-10秒,這當然與事實不符。他也強調洞的質量只能與電子相同,而質子遠重於電子。經過這一連串討論,狄拉克终於在1931年下定論:「洞是一種實驗中未發現的粒子,其質量與電子相同,電荷與電子相反。」即是說,負能量解其實對應反電子,能量為正(正如一切粒子),而兩個解對應上旋和下旋,即自旋 s=1/2,與電子的自旋相等。
安德森 (C. D. Anderson) 於1932年用雲霧室觀察宇宙射線,首次發現反電子。圖三為安德森所拍得的反電子在強磁場作用下於雲霧室中的軌跡照片。在該照片中,反電子從下進入中間的鉛板,喪失部份動能,然後從鉛板上方逃出。磁場方向垂直於相片,指入相片。粒子在鉛板下方的軌跡弧度比鉛板上方的軌跡弧度小,顯示粒子在下方的速度比上方大,即粒子運動從下至上。粒子軌跡在磁場下向左彎曲,顯示粒子電荷為正。從粒子穿過鉛板中的動能喪失和粒子軌跡的孤度和長度,安德森推算出粒子的質量與電子相約,並且電荷約為電子的相反。
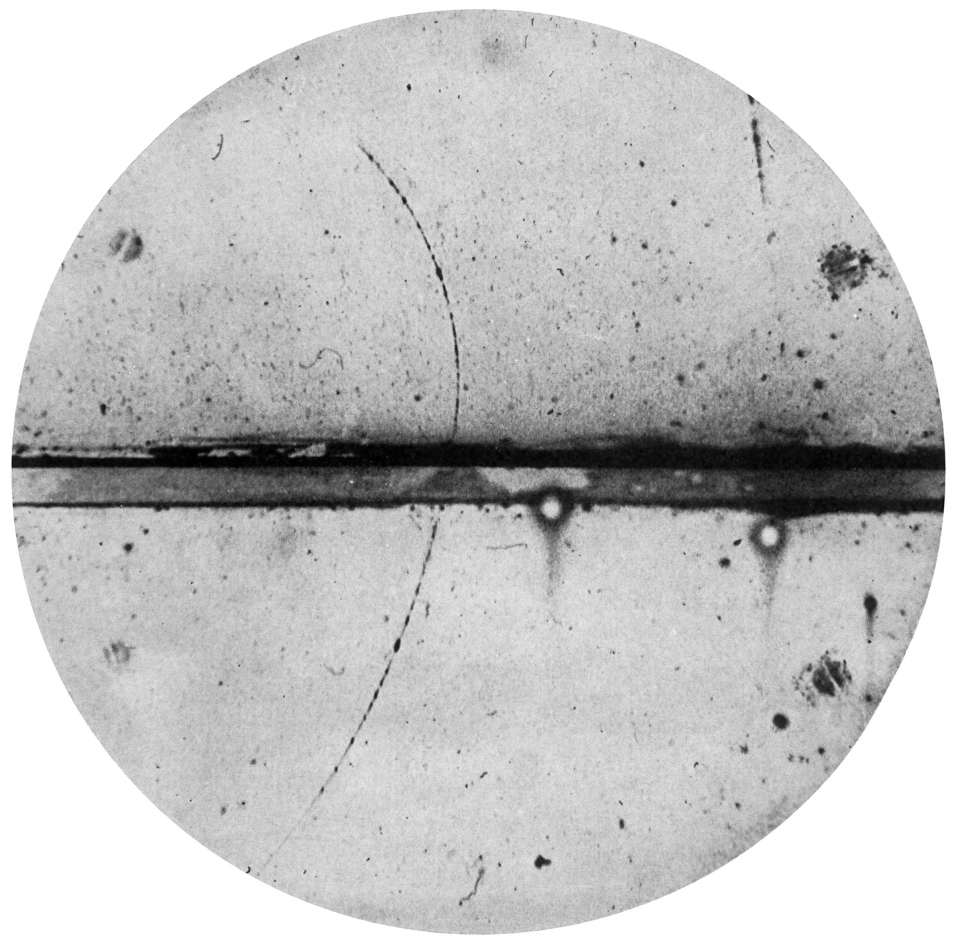
狄拉克因為發現狄拉克方程式和對正電子的預言獲得1933年諾貝爾物理學獎,而安德森因發現正電子而獲得1936年諾貝爾物理學獎。此後,各色各樣的反粒子在實驗中陸續被發現。值得注意的是,狄拉克方程中守恆量的正定性,只是一個經典埸方程的結果。從現代量子場論的角度看,狄拉克方程式應被視作量子場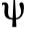 的運動方程,而
的運動方程,而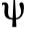 不是函數,而是算子。作為量子場的方程,狄拉克方程式的守恆量其實是電荷,其取值可正可負。有趣的是,狄拉克對守恆量正定性的不必要的堅持,驅使他發現了一條正確的方程。還有,安德森在發現正電子時,對狄拉克的理論並不熟悉,他只是專注於對宇宙射線的測量,所以正電子的發現可說是一場無心的美妙意外。
不是函數,而是算子。作為量子場的方程,狄拉克方程式的守恆量其實是電荷,其取值可正可負。有趣的是,狄拉克對守恆量正定性的不必要的堅持,驅使他發現了一條正確的方程。還有,安德森在發現正電子時,對狄拉克的理論並不熟悉,他只是專注於對宇宙射線的測量,所以正電子的發現可說是一場無心的美妙意外。
註解:
1)我們也會把粒子在離散時空對稱變換下的性質視為一種荷,如宇稱(未來會談到)。
2)弱同位旋的z分量T3是加法量子數,即複合粒子的T3是其成份粒子的T3的和。
3)正如第七章所述,夸克帶基本色荷,反夸克帶反基本色荷。
延伸閱讀:
粒子物理行系列文章