物理學的黃金原則:最小作用量原理

阿文過去長期擔任自己系上的圖書委員，任務之一是薦購書籍給圖書館買來當館藏。對於愛書的阿文來講，是個絕佳的機會能夠讀到許多新書的好機會。其中有一本書，阿文覺得真是太讚了，忍不住要來與各位看官分享。這一本是Alberto Rojo 與 Anthony Bloch 合著的 「最小作用量原理」(The principle of least action)。Rojo 是在奧克蘭大學(Oakland University)任教的理論凝態物理學家，而Bloch則是密西根大學的數學教授。這本書奇特的地方在於它不是一般的科普書，而是一本貨真價實的物理學專書，但是它卻縱貫了好幾個世紀，從古希臘幾何難題一路寫到二十世紀的相對論與量子力學。這些內容都圍繞在一個主題上，就是大家耳熟能詳的最小作用量原理。與一般科學史的書不同的是，這本書努力完整重現這些科學史上赫赫有名的材料，並沒有閃躲方程式，而是如實地呈現，就是這一點讓阿文耳目一新，大呼過癮。當然，這樣的寫法對一般讀者而言，門檻稍微高了一點，但是對學過微積分的朋友來說，應該游刃有餘。反過來講，對比較積極求知的高中同學而言，這本書也可以當作是微積分的入門書，因為它遠比一般微積分教科書有趣多了，而且，微積分本來就是因為物理研究的需要而被創造的嘛！

這本書的內容從有名的狄多女王(Queen Dido)的問題開始，在羅馬詩人維吉爾的《艾尼亞斯記》（Aeneis）中描寫狄多提供了大量的財富給住民，條件是交換可以圍在一張公牛皮內的東西。當他們同意這樁看起來很划算的買賣時，狄多將皮革切成條狀後，再將條狀牛皮連接在一起，變成一條很長的"皮帶"，狄多將皮帶圍住一個頗具戰略性的小山頭，這個山頭就變成她的。這個小山，便是日後的迦太基。姑且不論這個故事真偽，這個問題本身就吸引了古代眾多學者的注意。這個問題可以被表述為：在平面上所有周長一定的封閉曲線中，是否有一個曲線圍成的面積最大？如果有的話，是什麼形狀？大家都猜得到答案：圓。但是證明可沒那麼簡單。真正嚴格的數學證明要等到十九世紀才由瑞士數學家Jakob Steiner完成。

但是古希臘數學家Zenodorus 曾證明相同周長的三角形中，等腰三角形面積比非等腰三角形大，而凸多邊形的話，凸正多邊形的面積最大。這個證明的技巧被亞歷山大里亞的海龍(Hero of Alexandria)拿去證明反射的光要走最短的距離的話，入射角必需等於反射角。這個可以算是最小作用量原理的濫觴。


而伽利略在他的「兩門新科學」(1638)中嘗試用類似的方法討論最速下降線，但是沒有得到正確答案。倒是法國數學家費馬在1662年證明了光從不同介質間傳播的路徑是費時最少的路徑。雖然折射定律在1621年就被荷蘭學者Willebrord Snell發表，而笛卡兒在1637年在Dioptrique 也宣稱相同的結果，並加上他的模型解釋。


但是費馬卻是依照亞里斯多德式的自然哲學之要求，賦予光的行為一個合理的解釋。之後海更斯在1690年將費馬的證明簡化，寫進了他的Treatise on Light。將自然現象連結到某個最小值也頗為符合十七世紀的思想：造物者是最高明的創造者，所以不會浪費祂的能力。這個思想淵遠流長，然而在十七世紀前的數學能力，力有未逮，直到十七世紀，學者才逐漸有落實這個想法的數學能力。


論到十七世紀的數學高手，當然不能不提牛頓。牛頓在 「原理」的第二部中討論哪種形狀的物體感受到最小的阻力。雖然這些問題用牛頓發明的微積分來解都不困難，但是牛頓都使用傳統的幾何法得到答案。而且他沒發表在書上，卻另外寫在沒發表的論文裡，還是後人從他手稿中發現的。


接著作者花了一整章討論了牛頓的 「原理」中，如何從軌道的形狀與力心的位置來決定力的性質。這一章雖然與最小作用量原理沒有直接的關係，但是趣味性十足。我們很難想像，不用微積分，如何做到從行星的橢圓軌跡與力心是焦點來推得反平方律。內容只用到高中程度的幾何喲！


第四章重頭戲上場了。這一章從John Bernoulli 在1696年寫信向萊布尼茲挑戰的問題開始，這個問題就是有名的最速下降線(Brachistochrone，「最短」（brochistos）和「時間」（chronos）)。這個問題是探討在重力作用而忽略摩擦力的情況下，一個質點在一點A以速率為零開始，滑到一點比A低的B，該以何種曲線行進才能令所需的時間最短。萊布尼茲只花了一個星期就把答案寄回給John Bernoulli。John Bernoulli 回信給萊布尼茲，裡頭提供兩個解答。一種與萊布尼茲的解類似，另一個解則是活用光學的折射定律。


John Bernoulli接著向全歐的學者徵求解答，在1697年五月號的Acta Eruditorum 刊出五種解答，分明來自John Bernoulli，他的胸弟 Jacob Bernoulli，l'Hospital 侯爵，Ehrenfriend Walther von TschirnEhrenfriend Walther von Tschirnhaus 以及牛頓。牛頓的解答還是匿名寄來的，但是John Bernoulli 卻認出作者，他「從爪子認出獅子」。最速下降線的答案是什麼呢?就是從被海更斯在Horologium Osicllatorium 中研究得滾瓜爛熟的擺線(Cycloid)。
 

它是一個圓在一條直線上滾動時，圓邊界上一定點所形成的軌跡。海更斯當時發現擺線是等時降線(tautochrone curve或isochrone curve）的解答。所謂的等時降線是一種曲線，將一質點放置在此曲線上任一點使其自由下滑（不計阻力）至最低點所需的時間皆相等。當然海更斯用的還是傳統幾何的方法。本書詳述了萊布尼茲的原始解答與John Bernoulli的做法。John Bernoulli 將最快下降線想像成光通過無限多層的介質，因為粒子的速度與高度有關，由費馬的最快路徑就不難求出最速下降線的答案是擺線。無怪乎，John Bernoulli 的學生，法國學者莫佩爾蒂(Pierre Louis Moreau de Maupertuis )會在1746年提出 「最小作用量原理」。不過他的出發點卻是形而上學，甚至是神學。他宣稱，神不會做多餘的事。他嘗試說明質點通過兩個介質時的路徑會讓「作用量」趨於最小值。他的「作用量」是質量乘上速度再乘上路徑長。不過當時莫佩爾蒂提出這個原理時卻被指控剽竊，他的對頭Johann Samuel König 說萊布尼茲在1707年寫給Jacob Hermann 的信中就提出了這項原理。而與Maupertuis 為了夏特萊夫人而爭風吃醋的伏爾泰也趁機寫了小冊子挖苦莫佩爾蒂。然而König 拿不出萊布尼茲的信的原稿，所以莫佩爾蒂的好友尤拉反過來指控對手偽造文書。這件事鬧得滿城風雨，阿文日後會寫篇專文，還請各位看官指教。



說到尤拉，的確不愧是數學之神，他的「Finding Curved Lines having some Properties of Maximum and Minimum」可以稱得上是變分學的開山奠基之作，在這本書的結尾處，尤拉導出了著名的尤拉方程式，可以求出讓任何一個量的沿線積分達到極值的路徑。條件是始點與終點的位置固定。尤拉將質量乘上速度再對路徑長做積分當作「作用量」，再利用尤拉方程式導出行星的運動軌跡。謙遜的尤拉把「最小作用量原理」完全歸功給莫佩爾蒂，所以現在許多書還是採用莫佩爾蒂最小作用量原理。在此，我們可以發現，質點與光的行為都可以用變分來處理，只要把質點的”折射率”取為(m(E-V(x))^^1/2 即可。接下來，作者話鋒一轉，開始討論起弦與「最小作用量原理」的關聯。此時的「作用量」則變成動能減去位能，但是不是對路徑長作積分，而是對時間積分。這正是我們熟悉的拉格蘭日函數。但是等等，我們在下一章會發現，拉格蘭日的思路卻不是如我們想的一般喔。

 

由 雅各布·伊曼紐爾·漢德曼 - Kunstmuseum Basel, 公有領域, https://commons.wikimedia.org/w/index.php?curid=893656

第五章則是討論達郎拜(D’Alembert)與拉格蘭日的工作。這條思路較少被談起，但是頗為有趣，影響也頗深遠。首先要從「虛功原理」談起。亞理斯多德曾主張當秤處於平衡時，兩端的重量比與兩端到端點的比是互成倒數。這是槓桿原理的推廣。伽利略將這個主張推廣到斜面上的滑輪兩端放法碼，要達成平衡的條件是兩個砝碼重的比與斜面與高的比成倒數。逐漸地，學者發現靜力平衡的條件是物體受到的力乘上”虛位移”的乘積加起來必須為零。


"虛(virtual)位移”這個詞是John Bernoulli最早使用的，是物體在滿足幾何限制條件下能同時作出的無限小位移。第一個將這個原理用到動態的是John  Bernoulli的長兄Jacob Bernoulli，他在1703年用「虛功原理」研究雙擺的運動，而四十年後法國學者達郎拜討厭牛頓的”力"的概念，嘗試在「Treatise on Dynamics」提議新的動力學系統。以他為名的達朗拜原則雖然被表達成頗為難解的形式 (難解到原文被放到附錄！)但是後來被拉格蘭日表達成類似「虛功原理」的形式，更具體地講，是外力的虛功與質點質量乘上加速度再乘上虛位移相等。要注意的是，系統的每個質點的虛位移並不一定是獨立的，因為系統要滿足特定的束縛，等於是各個質點之間要滿足特定的幾何關係。如果每個質點都是靜止的話，那麼達朗拜原則就變回虛功原理，但是在一般動態的情況，則變回牛頓的第二定律：
F=ma。


拉格蘭日在他的鉅著「解析力學」中將達朗拜原則改寫成每個物理系學生都學過的拉格蘭日方程式。連帶的拉格蘭日函數也被引進來，而拉格蘭日函數最大的優點：容易掌握系統的對稱性，自然也被提到了。比較有意思的是連Laplace-Runge-Lenz向量也提到了。這是只有在反平方向心力作用下才守恆的物理量。


新奇的是，這本書還特定介紹了耗散系統以及非可積系統，因為這兩種情形都不能直接用「最小作用量原理」來處理，但是可以使用達朗拜原則，也就是拉格蘭日方程式來研究。所謂非可積系統指的是系統中質點的虛位移滿足的條件無法寫成質點位置之間的關係式。nonholonomic 這個詞還是德國科學家赫茲Heinrich Hertz 在 The principle of Mechanics (1894)中發明的。也是在這本書中，赫茲將高斯的最小束縛原則改寫成最小曲率原則。這些材料也都有提及。最後一個意外驚喜是James McCullagh在1839年提出的以太的拉格蘭日函數。以太被當作是一種有彈性的流體，瞭解了這個設定，對馬克斯威爾當年怎麼整合出完整的電磁理論，就不會一頭霧水了。這也稍稍彌補了本書沒有將電動力學放進來的遺憾。


第六章是全書最有份量的一章，應該也是對現代讀者來講內容最為陌生的一章。這一章的主角是漢密爾頓。雖說每個物理系的學生都學過漢密爾頓力學，但是對他的光學成就與所謂的漢密爾頓-雅可比理論(Hamilton-Jacobi theory)可就不那麼熟悉了。漢密爾頓的動機是要將光與質點都統攝在同一個架構下，最後的成果就是漢密爾頓-雅可比理論。


本章一開始介紹漢密爾頓如何用所謂的特徵函數(characteristic function)來處理幾何光學，第二節則是用特徵函數來處理雙軸晶體的錐狀折射。法國光學家菲涅爾研究過雙軸晶體，但是漢密爾頓的方法威力更強大，並且發現了菲涅爾沒注意到的新現象：錐狀折射，就是當光束沿其雙軸晶體的一個光軸時，這道光束將演變為空心的傾斜錐形，並且在離開晶體時，在介面發生折射，出射光形成錐面光束。


這個現象後來在1833年二月，被漢密爾頓在都伯林的同事Humphrey Lloyd 確認，使得漢密爾頓名聲大噪。但是這些光學成就只是漢密爾頓宏偉計畫的一部分。接下來漢密爾頓尋找力學的特徵函數，並且定義「主函數S」(principal function)，由此寫出漢密爾頓-雅可比方程式。漢密爾頓還利用特徵函數來處理行星繞日運動。接著漢密爾頓從新推導出拉格蘭日方程式，但是與拉格蘭日不同，漢密爾頓是對主函數作變分而得。今天，漢密爾頓的作法已經成為教科書的標準作法了。接下來定義與座標共軛的動量，以及將拉格蘭日方程式改寫成動量與座標的一次方程式(現在稱之為漢密爾頓方程式)的作法也是標準教科書的材料。但是教科書沒有的是把漢密爾頓-雅可比理論與海更斯原則放在一起。


漢密爾頓注意到以波動意象為主的海更斯原理與以粒子意象為主，利用變分學的費馬原則是等價的，同理，利用變分學的最小作用量原理也應該存在對應於海更斯原理的理論存在，那正是漢密爾頓-雅可比理論。只要把特徵函數的值等於常數的曲面當作是波前即可！ 接下來作者給了幾個漢密爾頓-雅可比理論的實際應用，像是簡諧振子與帶電粒子在磁場下的運動。但是令人眼睛為之一亮的是最後一節討論的是物理路徑並非讓「作用量」達到「最小」的實例。在光學中這種例子俯拾即是，只要把終點放在焦點後面，很容易發現光的路徑並非最短路徑。但是雅可比是第一個討論在力學裡類似的例子,連帶地作者也介紹了Gouy’s phase 與光學的焦散(Caustics) 焦散是由曲面或物體反射或折射的光線的包絡線，也是光強度最強的地方，Caustics是希臘文，原意是燃燒。這是因為光強度最強處可拿來點燃之故。這些都是一般教科書沒提的有趣內容。


接下來兩章則是分別是「最小作用量」與近代物理的兩大支柱：相對論與量子力學的關係。第七章前兩節是簡明的特殊相對論介紹，最後引進了相對不變性的「作用量」，以即相對不變性的漢密爾頓-雅可比方程式。後三節則是與廣義相對論相關。作者特別關注光被重力偏折的現象。他用了兩種方法，第一種方法是利用等效原理，第二種方法則是利用Laplace-Runge-Lenz 向量。得到相同的結果，但是這只是正確值的一半。當然，作者也提供廣義相對論的作法。此外，水星近日點的異常也都有提到。最後一節是關於希爾伯特如何利用數學的要求建構「最小作用量」，輕而易舉地導出愛因斯坦重力場方程式。




最後一章是討論「最小作用量」與量子力學的關係。這一章包含了許多科學史的好材料,而且往往是與原始文獻吻合。像是大家耳熟能詳的波爾模型，通常都沒提到波爾如何利用”對應原則”來推理的過程，而是直接假設角動量的量子化再加上量子躍遷，但是在本書，作者卻是很小心地重現波爾原來的思路，光是這一點就讓阿文感覺超開心了。後頭還有索末菲將波爾模型推廣到橢圓軌道，並且將特殊相對論的效應考慮近去得到氫原子光譜的精細結構。此外，作者還特地花了一節介紹舊量子論的漸緩不變量(adibatic invariants)。早在1911年第一次索爾維會議時，羅倫茲問愛因斯坦，如果一個單擺，懸點不動，擺長隨著時間變化，那麼它的能量能量子化嗎?愛因斯坦當時回說，單擺擺長變短，周期變短、能量變大，只要擺長變化夠慢，能量與周期乘積不會改變，換言之，能量與頻率的比不變，那麼能量量子化的條件還是可以維持。這個說法後來被Paul Ehrenfest 具體化成漸緩假設(adiabatic hypothesis)也就是漸緩過程中不變的量要量子化。 Ehrenfest 的證明也放在附錄裡。
 

由 JabberWok, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2639910
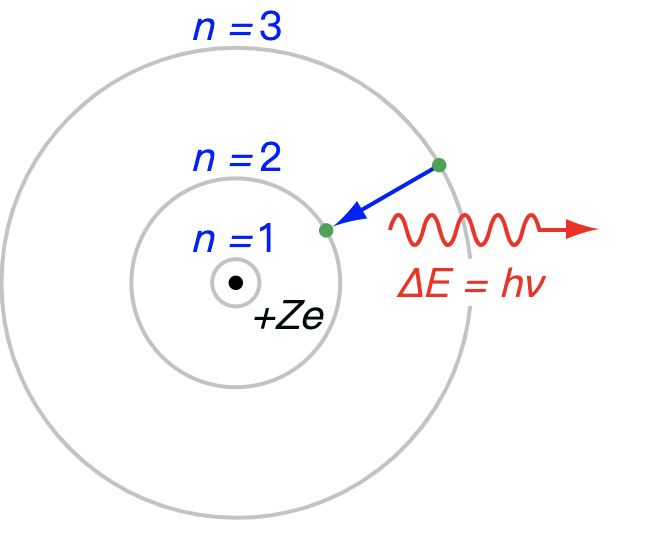
在波耳模型裡，被約束於原子殼層的帶負價電子，繞著帶正價原子核進行圓周運動。從一個軌道躍遷至另一個軌道會伴隨著離散能量以電磁波的形式被發射或吸收。[1]在圖中，電子的軌道顯示為灰色圓圈，其半徑隨著主量子數平方n²增加，從主量子數3 → 2的躍遷製成了巴耳末系的第一條譜線，波長為656 nm （紅光）。

不過這些舊量子論的花絮比起後面的內容只能算是小菜一碟。這一章的大菜是赫赫有名的薛丁格方程式。當德布羅伊意想天開地提出物質波的假設之後，在蘇黎世的奧地利籍物理學家薛丁格認真地推敲，他的主要靈感是來自於1911年索末菲與Runge 的一篇文章。在這篇文章中，他們對波動方程式取短波長的極限，得到了類似漢密爾頓-雅可比方程式的Eikonal 方程式。薛丁格將整個推導倒過來，得到了漢密爾頓-雅可比方程式對應的波動方程式，就是薛丁格方程式。實際上，對薛丁格方程式取古典極限(h→0)就會得到漢密爾頓-雅可比方程式。接著討論的是量子力學的路徑公式，這是為了最後一章鋪陳。最後的一節的主題又回到海更斯原則。只是這裡討論的是在量子力學中的海更斯原則。有趣的是二次微分的波動方程式被寫成兩個分量的一次微分方程的形式。雖說路徑積分的公式精神上與海更斯原則很接近，但是與漢密爾頓-雅可比方程式不同的是，在量子理論中，薛丁格方程式的解無法當作波前處理，這一段可就新奇了，細節還得請各位親自去讀。


這本書篇幅不長，就只有兩百多頁，但是內容涵蓋了上下兩千年，用最小作用量這根線將古典力學，光學，相對論與量子力學串在一起。而且內容是真槍實彈的計算，而非只是虛晃一招地說說而已。書後面還有九段附錄，把細節都給交代了。有機會的話，阿文希望有朝一日，拿這本書開門課，應該會是相當有趣的經驗吧。順便一提的是，這本書也很適合搭配Herbert Goldstein 的那本堪稱經典的古典力學一起來讀，會有意想不到的收穫喔！