深度學習及其在凝態物理上的應用 – 中篇: CNN與RNN

在上一篇文章中，我們簡單介紹了深度學習的觀念以及歷史，然而我們並沒有提及深度學習中最重要的兩個基本架構，也就是卷積神經網路(convolution neural network)以及循環神經網路(recurrent neural network)。這兩個神經網路分別用來處理了對空間有關聯性的數據以及時間有關聯性的數據，前者後來被廣泛地使用在影像識別上，後者則被廣泛地使用在自然語言處理以及時間序列等問題上。有了這兩個強大的武器，當代深度學習大爆發才有了牢固的基礎，因此要講深度學習，核心問題就是要理解這兩種神經網路架構。

卷積神經網路

 

卷積神經網路的雛形其實很早就被提出了，早在1989年，當時人在AT&T 貝爾實驗室(Bell Lab)的Yann LeCun(現在Facebook AI實驗室首席科學家)就已經提出使用後向傳播對卷積層做訓練的想法了[1]，但是當時並沒有引起廣泛的注意，這時候的卷積神經網路還很陽春，也缺乏池化層的觀念。真正近代卷積神經網路被提出，則是1998年的事情了。1998年時，LeCun在重新鑽研了卷積神經網路近十年後，提出了一個全新的架構，也就是後來被稱為的LeNet-5的卷積神經網路架構[2]。在這個版本裡，LeCun引入了局域相連，共享權值，池化壓縮等先進的觀念，奠定了當代卷積神經網路的基礎，也因此被稱為卷積神經網路之父。也因為LeNet-5的提出，這才提供了足夠的養份，讓Hinton等人在2012年提出了AlexNet終於把神經網路徹底脫胎換骨成了當代深度學習，所以LeCun苦心鑽研了20多年的問題總算皇天不服苦心人，終於奠定了他一代大師的地位。然而講到這裡，讀者可能還是很疑惑到底什麼叫做卷積神經網路? 下面我們來好好講講什麼叫做卷積神經網路。要理解卷積神經網路，就得從影像的操作不變性講起。

 

穩定性是個問題

 

“ 卷積神經網路最早的出發點是為了處理影像識別的問題，然而要電腦長眼睛，看得懂圖片是一件談何容易的事情。”

首先要面對的問題就是影像數據的穩定性的問題。就拿一張圖片，上面有個手寫數字3好了，我們怎麼把這個數據輸入到神經網路中呢? 最直接的方法就是把這張圖片的每個pixel的數值作為神經網路的輸入。以一張28x28 pixel的256灰階圖片為例，這樣一張圖片總共就會有784個pixel，每個pixel可以取值0~255(256灰階)，所以我們就可以把這樣圖片拉直成一個784維的向量，每個向量的元素可以介於0~255之間。但這樣的操作馬上就會引起一個問題：穩定性！

 

以下面附的圖為例，同樣是3，我們可以寫在圖片的不同角落，對人來說都是3，但是如果我們使用了上述的操作，即便兩個3是完全一樣的3，但是建構出的向量則會長得完全不同，這樣的操作叫做平移(translation)。除了平移之外，我們還可以對這個3進行縮放(scale)，旋轉(rotation)，甚至把這個3個形狀做一點改變(deformation)，這些都是3，可是卻會形成了完全不一樣的向量，這會造成模型訓練的十分困難，但是我們又沒有好的方法能夠告訴他這個3跟那個3其實是一同一個3，他們的差別只是被執行了一些空間上的操作而已。也因此影像識別形成了一個挑戰極高的領域。

 

圖一：影像處理中常見的導致神經網路不穩定性的操作

 

在LeCun提出的LeNet-5中，他提出了讓卷積層搭配池化層共同作特徵提取來增加神經網路的穩定性。所謂卷積層的觀念其實很簡單，考慮我們有一個28x28的256灰階圖片，那麼我們可以把他表示成一個28x28的矩陣，然後我們再定義一個3x3矩陣(或者其他大小，一般常用的有1x1, 3x3, 5x5，該用哪個則有賴於對於測試數據的結果好壞來決定)，我們就讓這個3x3矩陣由左到右由上到下的每次移動一步去掃這個28x28的矩陣，這個28x28的矩陣中被掃到的區塊就跟這個3x3矩陣做矩陣的元素相乘(elementwise-product)，乘完的結果會得出一個新的矩陣，這個過程就叫做”卷積“（這裡說的卷積其實跟數學上的卷積定義其實不同，但觀念類似），而那個3x3矩陣稱作卷積核(kernel)。那麼我可以創造很多個這樣的3x3矩陣，每個矩陣的數值都不盡相同來做同樣的事情，我就可以同時得到大量的卷積完的矩陣，這就是卷積神經網路的卷積層在做的事情。當然馬上有人會問，這些拿來卷積的矩陣的矩陣元素是如何得出的？答案是靠後向傳播得出的。也就是說在訓練剛開始時，我們先隨機產生一堆這樣的3x3矩陣，然後再透過前一篇文章中提到的後向傳播透過誤差修正來得出最佳的矩陣元素。至於卷積層的功用到底是什麼，為什麼要設計這樣的神經網路層？這問題我們留待後面再回答。

 

 

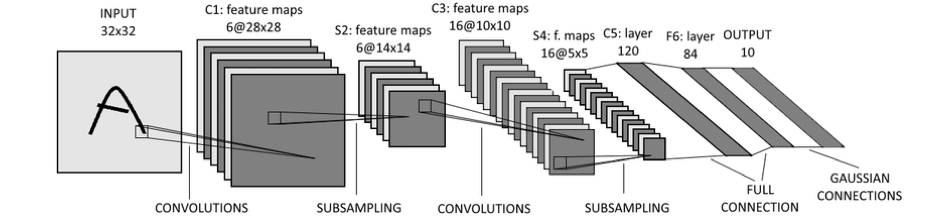
圖二：1989年由LeCun提出的LeNet-5架構


 

在LeNet-5中提出了另外一個重要的操作就是讓卷積層搭配池化層來做堆疊，而所謂的池化層很簡單，當我們有一個矩陣，例如28x28，我們就定義一個大小例如每2x2為一個單位，然後我們在每個2x2的子矩陣中取出一個最大的值(或是平均值) 來代表這2x2矩陣的訊息，所以原本的28x28就變成了14x14了，每個矩陣元素是原本那個28x28矩陣中每2x2為單位取出的最大值，這個過程就叫做池化。

 

所以LeNet-5的基本架構其實很簡單，先把圖片以矩陣的形式輸入，然後卷積-池化-再卷積-再池化，最後把結果拉直成一維向量然後送進一個全連結神經網路中，最後做機率輸出，整個神經網路就完成了。這架構雖然簡單，但是一下子把影像辨識的正確率拉高了不少，成就近代卷積神經網路的基礎。

 

然而這樣的操作為什麼會有效？這就要回到我們前面提到的穩定性的問題。

 

為什麼卷積神經網路有效

 

現在我們再回到前面的問題，到底卷積層跟池化層解決了什麼問題？首先我們來看卷積層。當我們選定了一個卷積矩陣，這就意味著被卷積的輸入圖片中，只有某些數值分佈才會有比較強的反應，換言之，這個卷積矩陣其實扮演了一種濾鏡的角色，他把圖片中的一些特徵給篩選出來。因此即使要被識別的影像是分佈在圖片中的不同區域上，又或者影像只是有些微程度的形變，透過這個濾鏡我們都可以把它的凸顯出來讓神經網路知道究竟這個圖片中存不存在某種特徵，所以縱然圖片可能不盡相同，但透過卷積層，至少我們可以了解到某種特徵(圖片中的某些邊，角，花紋等結構)存不存在這張圖上。此外也由於我們在使用濾鏡掃整張圖片時，在不同的區域我們使用的都是同樣的數值，也大幅減少了參數的數目避免了過擬合。正是這個局域連結(用濾鏡掃整張圖片的不同區塊)以及權值共享的觀念，讓神經網路對影像的平移以及形變這些問題有了一定程度的緩解。

 

那池化層呢？池化層因為在小區塊中只提取出最強的特徵出來，這相當於讓神經網路對於小範圍內的形變，縮放以及平移等操作更具有穩定性。此外大家應該也不難想像，池化這個操作再進行了多次之後，矩陣會逐漸變小，這相當於不斷的把神經網路的視野拉遠，從一開始只提取局域的特徵到後來逐漸擴大視野，看到了全域的特徵。就是這樣的搭配導致了卷積神經網路對影像識別有了超乎尋常的表現，後來在AlexNet中引入了Relu進一步把網路做深，在加入Dropout解決過擬合，以及GPU計算來加速，最終促成了當代卷積神經網路的誕生。這一切的轉變，LeCun可謂功不可沒！

 

循環神經網路

 

講完了卷積神經網路，我們就要接著講循環神經網路了。卷積神經網路主要在處理空間關聯性的問題，也就是說這些pixel的值在那個28x28的矩陣上的分佈是具有意義的，一但你打亂了，意義就消失了，這就是一種空間上的關聯性。但是很多數據是在時間上的分佈有意義的，例如語言，你把一句話的文字隨意的調換意義就失去了，又例如時間序列，你把股市的價格波動全部打亂，就變成了一堆不連續的線段了，也就完全失去意義了。那我們該怎麼處理這樣的問題呢？這時候就仰賴循環神經網路了！

 

“ 其實循環神經網路跟卷積神經網路的精神是類似的，唯一的區別在於卷積神經網路是在空間上卷積，而循環神經網路是在時間軸上做卷積，此外由於循環神經網路是在一個一維的時間軸上進行卷積，因此並不需要引入池化層以及二維的卷積核。除了這些差異之外，兩這個差異並不大。”

 

考慮我們有一個時間序列的數據，在每個時刻t時會輸入一個向量，這個時候我們可以定義一個全連結神經網路D，每次就接受這個向量x(t)的輸入然後輸出另一個向量x’(t)。當下一次x(t+1)輸入的時候，我們要把上步的輸出x’(t)一起作為輸入，然後來輸出x’(t+1)，這就是一個循環神經網路的架構了。所以每一步的輸出除了時刻t的輸入還有上一步輸出一起作為輸入來預測輸出，這就確保了每個時刻t時，神經網路不僅僅有當前的資訊，還包含了過往歷史所累積的資訊。這個過程可以簡單的表示成如下的圖示。

 

 

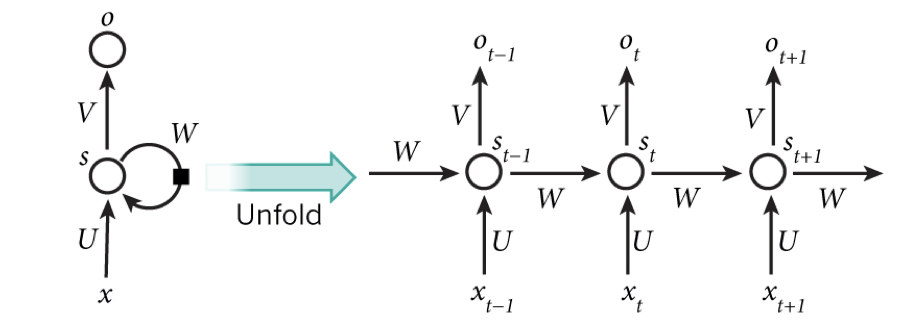
圖三：ＲＮＮ的網路神經示意圖

 

要注意的是，對每個時刻神經網路的如同卷積神經網路一樣，參數是共享的。這個想法簡單，而且最大程度的保留了神經網路的過往資訊，然而實際上的表現卻十分不好，最主要的問題在於我們前面提過的梯度消失的問題。

 

在使用RNN時，一般我們選用的激勵函數是sigmoid，前面我們已經提過了，這樣的函數會導致神經網路的梯度無法回傳，造成訓練上的困難。同樣的問題在RNN裡面則會反映在神經網路總是只能基於輸出前的一兩個時刻的輸入作梯度修正，無法保持長時間的記憶，因此RNN的發展可以說是困難重重。

 

長短時記憶網路

 

前面我們提到，LeCun在1998年的時候提出了LeNet-5，奠定了當代卷積神經網路的基礎，就在差不多的時間，在大西洋的彼岸有兩位德國科學家Sepp Hochreiter與 Jürgen Schmidhuber也在RNN上作出了重大的突破，這就是長短時記憶網路(long short-term memory network, LSTM)[3]。Hochreiter與Schmidhuber意識到造成低度消失的主因就在於矩陣乘法以及激勵函數的不斷堆疊，因此如果在神經網路中另外設計一個資訊流動的網路，在這條網路上避開所有的矩陣乘法以及激勵函數，那麼誤差修正在這條線上回傳的時候就不會再遇到梯度消失的問題了，這條線就稱作long term memory。

 

 

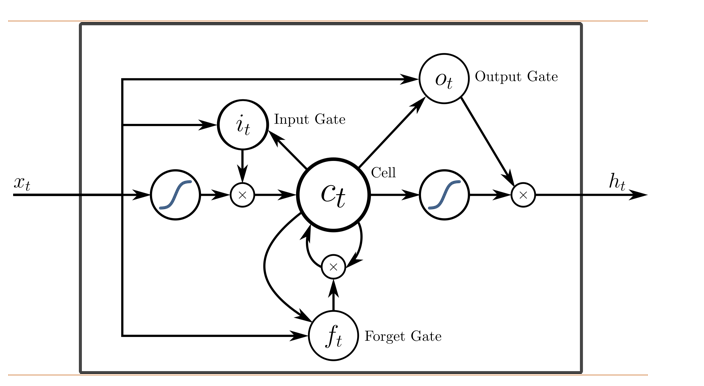
圖四：ＬＳＴＭ架構示意圖

 

但是這條長時記憶線又該怎麼跟正常的RNN之間溝通訊息呢？經過他們多方的嚐試，他們設計了三個”門“，這裡所謂的門，指的就是一個矩陣的元素相乘，所以正常的RNN跟常時記憶線間的訊息流通就是透過這三個門來決定的，他們分別設計了三個門：輸入門，遺忘門，以及輸出門。輸入門透過了一個陣列相乘(element-wise product)決定了哪些資訊要從輸入傳入長時記憶線中，反之，遺忘門則決定的哪些資訊要從長時記憶線中被丟棄，而輸出門則決定了哪些資訊最後要被匯入到下一個時刻中作為初始化的輸入。所以LSTM的機制可以想像成我們有一部電視劇，每一集裡面會有些角色登場，但不是所有的角色都和下一集有關聯，所以我們透過一個長時記憶線來保留那些要一路往下走的角色跟劇情，如果某一集有新的角色登場了，而這個角色在後面的集數中還要再出現，我們就先透過輸入門把這個角色先”存“在長時記憶線中，反之，有些角色這一集就消失，之後不會再出現了，我們就透過遺忘門來把這個角色刪除，最後有些角色在之前的集數中被保存在長時記憶中，而下一集要用到它了，我們就透過輸出門把這個角色”提取“出來送到下一集中，就這樣透過這三個門的搭配，我們就可以設計一出一個能夠保留很長的序列記憶的神經網路了。

 

從現代神經網路的觀點來看，Sepp Hochreiter與Jürgen Schmidhuber兩人的設計是極富巧思的，他們處理梯度消失的問題並不是從激勵函數下手。他們當然也理解到梯度消失的原因和激勵函數的選擇息息相關，但他們選擇了使用一種更充滿想像力的方式來處理這個問題，從現在看來，LSTM仍然是一個十分精巧的設計，時至今日也少有能超越的作品。

 

值得一提的是，Schmidhuber本人對各種科學主題都非常著迷，包括物理學，多重宇宙等等，他甚至發表過一篇長達50頁的文章發表他心中基於計算機科學角度的宇宙大統一理論[4]。但有別於深度學習三巨頭：Hinton，LeCun以及Benigo所獲得的巨大注意，Schmidhuber曾多次抱怨過他沒有在AI界獲得應有的注意與尊重，甚至為此和LeCun互相責罵過一番，不過這些茶餘飯後的軼事在此就不多討論了。

 

結語

 

在這篇文章中，我們進一步的討論了深度學習中最重要的兩個基礎神經網路架構：卷積神經網路以及長短時記憶網路。這兩個網路被分別用來處理了與空間以及與時間有關的數據，不過至此讀者可能仍會困惑，究竟深度學習在凝態物理上能夠怎麼應用，在下一篇文章中，我將會帶領大家系統的回顧過去幾年深度學習在凝態物理上應用的幾篇論文作為本期專題的結束。
 

---

延伸閱讀
深度學習及其在凝態物理上的應用 – 上篇：什麼是深度學習
深度學習及其在凝態物理上的應用 – 下篇: 深度學習與凝態物理 

 

---

想要訂購並贊助物理雙月刊的朋友請走這裡：

一年份訂購：https://cashier.ecpay.com.tw/store/3rg26
電子雜誌租購：https://ebook.hyread.com.tw/bookDetail.jsp?id=163393
紙本雜誌單本訂購：https://www.books.com.tw/products/R030078974

 

參考文章

[1] Y. LeCun et. al., Neural computation 1 (4), 541-551 (1989)

[2] LeCun et. al., Proceedings of the IEEE 86 (11), 2278-2324 (1998)

[3] LSTM: Sepp Hochreiter & Jürgen Schmidhuber, Neural computation 9 (8), 1735-1780 (1997)

[4] Juergen Schmidhuber, arXiv:quant-ph/0011122 (2000)