意外的強相關聯材料 --- 魔角雙層石墨烯

摘要

厚度只有一個原子大小的石墨烯，除了作為拓樸絕緣體的基本模型外_[1]，其絕佳的導電以及應力特性也成了材料、化學與光電等應用領域的重要議題。價電子佔據p軌域的碳基材料幾乎不被認為是超導材料，更與強關聯系統沒有太大關係。最近一期自然雜誌連續兩篇論文_[2,3]報導魔角雙層石墨烯 (Magic Angle - Twisted Bilayer Graphene 簡稱 MA-TBG) 材料中發現的超導與強關聯物理：費米面附近的能帶有極小的能帶寬度，並且當改變載子濃度到半填滿狀態時，所量測的電導大幅下降；此外這材料的溫度-載子濃度 (temperature-carrier density) 相圖更透露出與高溫超導許多相似之處。本文將簡單介紹魔角雙層石墨烯的基本物理，其費米面附近所形成的平能帶_[4](flat band，能帶與動量關係 E(k)為一定值)，以及簡單的物理圖像來理解實驗結果。

 

前言    

 

2010年的諾貝爾物理獎頒發給兩位第一個成功製造出石墨烯 --- 只有一層原子厚的碳材料 --- 的兩位英國物理學家。由於它極佳的導電與機械特性，石墨烯的研究與應用已出現在數不盡的物理、化學、生物、醫學的基礎與應用領域之中。對於材料基礎物理研究，石墨烯更是過去十年內研究的最熱門議題：量子霍爾效應、局域現象、傳輸特質、多體物理與光電特性等都和傳統的二維電子氣中所發現的現象極為不同。這些不同都可歸因於能帶結構的基本差異：一般的二維電子氣 (如三五族異質材料介面) 的能帶關係是非相對論性的二次關係 (E=p²/2m)，而石墨烯的能帶關係則與光子一樣或者是相對論性的線性關係 (E=pc)。

 

儘管在各個領域被廣泛的討論，石墨烯這樣的材料很少被認為可以作為研究強關聯電子物理的系統。強關聯物理指的是電子與電子之間的庫倫作用力無法被忽略，比如過度金屬氧化物中所展現的磁性質，或者是銅氧化物中所展現的量子相轉換 (quantum phase transition)，都無法被現有的費米理論 (Fermi liquid theory) 和平均場論 (mean field theory) 所解釋。石墨烯以碳原子為骨架，它的價電子佔據p軌域，比起d軌域的電子有較廣的波函數分佈，故p軌域的價電子就比較像真空裡面的自由電子，只需要把有效質量做修正，許多傳輸性質都可以被Drude model成功解釋。可是別忘記物理中很重要的概念：任何物理量的大小都是相對的！庫倫作用力的大小要跟什麼物理量相比？在固態系統中，能帶寬度 (band width) 是一個非常重要的參數：在銅氧化物中，費米面附近的能帶寬度比起庫倫交互能 (約數個電子伏特) 小得多，所以是一個典型的強關聯材料。那如果p電子佔據了能帶寬度很接近於零或者是很小的能帶，那庫倫作用力也會變得非常重要！這個關鍵的平能帶可否存在於石墨烯這樣的二維材料中？早在2007年，就有一組理論學家開始研究雙層的石墨烯彼此之間有一個旋轉錯位角度 (twist angle)，經由上下層的碳原子軌域混成，可以改變狄拉克點附近的費米速度_[5]。這樣的想法在2011年，另一組理論學家更進一步發現，在某些特殊角度 --- 魔術角度 (magic angle) --- 的旋轉錯位下，費米速度甚至能降為零，如圖一 _[4] 所示，在費米面 (能量等於零處) 附近，形成完全平坦的能帶 (flat band) _[4]。

 

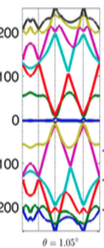
圖一_[4]

 

庫倫作用力的角色在平坦的能帶中變成很重要，這早已在分數量子霍爾效應中被印證過：二維電子氣系統下，外加垂直磁場迫使電子被侷限在圓周運動軌道上，在極大磁場下，電子之間的庫倫作用力，決定了電子的動力學。對熟悉量子力學的讀者而言，磁場像是製造出一個零能寬的系統，所有電子的動能都被限制了！下面的篇幅將帶領讀者簡單了解 MA-TBG 結構下可調變的能帶結構：當上下層具有某些錯位角度 (twist angle) 時，上下層的p軌域混成的結果使得費米面附近形成平能帶或是小能寬能帶。這兩篇論文中報導的實驗，就是利用精準的石墨烯成長技術，加上二維材料本身可以利用外加電場來控制載子濃度，所以能找到一些證據來支持他們的發現 --- 強關聯性質的絕緣態。強調強關聯性質的意思是這樣的絕緣態，是無法經由能帶結構所推論出來。

 

Moiré 超晶格與平能帶

 

單層石墨烯的結構可以由兩個碳原子 (通常稱做A和B碳原子來區別) 所組成的單位來描述。把這個基本單位無限制的週期延伸出去便形成了石墨烯，且經由簡單的能帶計算 (比如tight binding model)，如果把能帶圖畫出來，像是有兩個冰淇淋甜筒上下接觸在一個點上，且在布里淵區之中，有兩個互相獨立的接觸點，理論學家一般稱作狄拉克點 (Dirac point)，而實驗學家通常稱做中性點 (charge neutral point)。當兩層石墨烯上下疊在一起，就可以有很多不同的新結構，且每一結構都有極為不同的能帶結構，也因此會有非常迥異的物理特性。這裡我們討論圖二的雙層結構：把兩層石墨烯上下完全重合疊在一起，然後對著中心點把上層做一個小角度的旋轉[2]。如圖所示，上層與下層的AB碳原子，有些地方完全重合 (A接A，B接B，這區域被稱為 AA-Stacking，並對應到比較能看清楚白色背景的區域)，而有些地方是上層A接下層Ｂ (這區域叫AB-Stacking，這對應到比較看不清楚白色背景的區域)。且這樣的區域形成了更大的週期結構：原本每一層的石墨烯的單位週期是原子尺度，但是雙層的單位週期則可以到奈米尺度。這樣新的週期模式組成稱為莫瑞 ( Moiré ) 超晶格，有興趣的讀者可以在youtube上搜尋關鍵字 ( Moiré pattern) 找到許多有趣的影片。
 

 

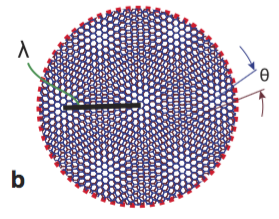
圖二[2]

 

除此之外，形成超大週期的結果就是原本單層石墨烯的能帶結構被切割且重組，且原本單層石墨烯的布里淵區 (大小反比於鄰近碳原子間的距離) 也縮小 (大小反比於 Moiré superlattice的週期，約數十倍到百倍大於鄰近碳原子距離)。而就能帶結構而言，也產生非常有意思的變化。圖三(i) 利用一個簡單的物理圖像來理解能帶結構的演變[2]。最左邊的能帶顯示兩層之間沒有任何交互作用，因為旋轉角度的關係，兩個狄拉克能帶在水平方向被錯開一個距離 (在反空間中這個距離正比於旋轉角度twist angle)，這背後的意思是電子的波函數只會分佈在其中一層，沒有機會使得電子能從下層穿隧至上層，或者上到下，基本上就只是兩個互不相干的單層石墨烯。圖三 (ii)則顯示當上下層的耦合能量 (w) 不為零但是很小的狀況，這個狀況下，主要被影響的區域就是兩個狄拉克能帶重疊之處。因此當電子的能量接近重疊的區域時，其波函數就會形成上下層的混合態，意指電子在水平方向移動時可以在上下兩層間任意的來回。這樣的軌道混成也造成能帶的分裂，且分裂的大小也與耦合能量w同一數量級 (標示為2w之處)。另一個間接的影響是費米速度 (Fermi velocity)的減小，意即能帶在狄拉克點附近的斜率 --- dE(k)/dk  --- 因為上方能帶被擠壓到較低能量，使得斜率變小。也由於 Moiré superlattice的對稱性與原本單層石墨烯相同，這上方能量壓縮所造成費米速度降低也是均向性。因此，在圖三 (iii)的圖示裡，當耦合能量 w 變得更大時，整個能帶被壓縮得更厲害，進而造成了平能帶的產生！在真實空間中，這些平能帶所對應的波函數顯現出電子被侷限在上下層為AA-stacking的區域，讀者可以把Moire superlattice想成一個新的三角晶格，每個頂點如圖四所示_[2]，由AA-Stacking的區域組成，電子因為無法跳躍至鄰近的頂點，使得能帶寬度接近於零 (如tight-binding model中跳躍參數 t 接近0)。最後一個觀看重點是能帶的簡併數 (degeneracy)：簡單來說是 4 = valley × spin，複雜的說由於 Moiré superlattice的尺度很大，所以可以耦合K和K’兩個相差甚遠的狄拉克點的微擾是可以忽略的。而這代表當載子密度的改變為 4/A (A為 Moiré superlattice的單位晶格面積)，就有一整個band被填滿或是清空。下面的篇幅我們將關注當濃度改變為2/A (約正負1.4x10¹²cm^-2)時，魔角雙層石墨烯所展現出奇特的物理！
 

 

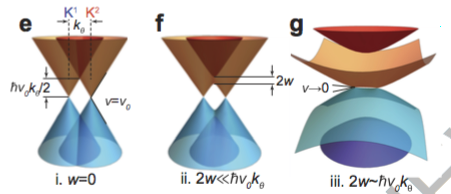
圖三_[2]

 

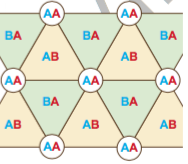
圖四_[2]

 

半填滿下的絕緣態

 

圖五顯示改變載子濃度下測量到的電導值_[2]。較為淺色且寬的陰影區顯示出當密度改變達 4/A 附近時，電導的數值幾乎降為零，這代表材料此時為一絕緣體；此發現與其他實驗的結果一致，因為能帶計算下，魔角石墨烯的確有兩個能隙在那附近產生，所以這部分沒有太驚奇之處。有趣的事發生在密度改變為 2/A 附近時，電導降為零的現象也發生，這從能帶結構無法解釋，因為一個半填滿的能帶對應到金屬的導電特質！在真實空間中，半填滿的能帶對應到單位晶格裡兩個頂點 (AA-Stacking處) 各多有一個電子佔據，但因為庫倫作用力 U 遠大於跳躍能量 t 的關係，這些電子選擇待在同一地點，進而使得傳導困難！
 

 

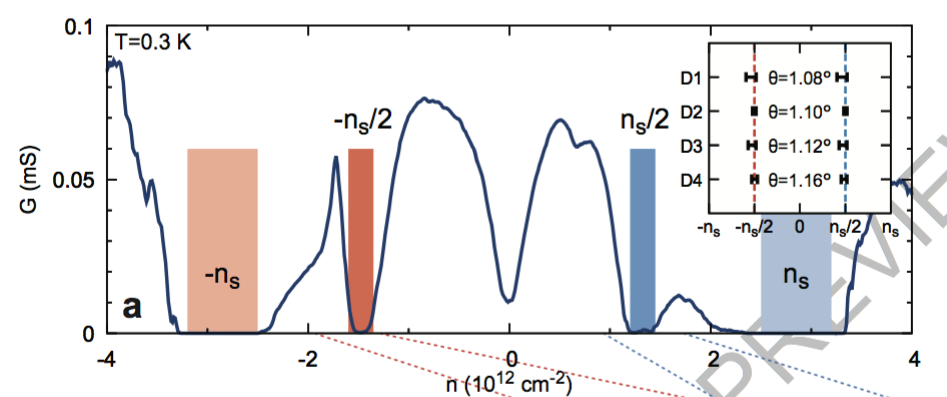
圖五_[2]

 

但如何證明這絕緣現象是因為電子庫倫互斥力所造成？這篇論文的作者測量雙層石墨烯的電容大小。把這個材料想像成上下兩片平行電板，電容的大小刻畫這電板上能擠多少電子。普通物理給我們的觀念是電板的面積越大，則電容也相對增加。但如果電子間的互斥力不可忽略的話，則固定面積的電板勢必無法容納一樣多的電子數目，意即電容大小應該是降低。如圖六所示，在低溫下 (0.3 K) 的量測，藍色所代表的數據的確在濃度約為 2/A 時有顯著的下降；且一旦升溫至 2 K，此一效應則消失。這證明低溫下，電子的確形成一強相關聯態[2]。
 

 

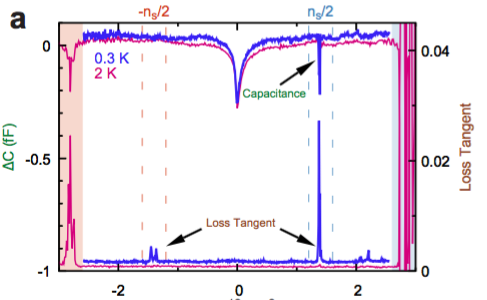
圖六_[2]

 

非典型超導

 

如果要判斷某一固體是否為超導所做的操作是把在高溫下是金屬態的材料降溫，如果發現電阻從緩降變成陡降且接近零時，就形成超導體，所對應的零電阻溫度就是轉換溫度。當然，最明確的證據是在磁場下材料是否展現完美的抗磁效應 (Meissner effect)！圖七顯示魔角雙層石墨烯所展現的電阻與溫度變化關係，說明了在1 K以下，這個材料變成了超導體[3]。比起我們知道的高溫超導體，轉換溫度大約在150 K左右，這個材料的轉換溫度相差了兩個數量級！但是這兩篇論文強調的是這個材料只需要的載子濃度是目前的最低紀錄，所以如果把轉換溫度比上費米溫度 (正比於載子濃度)，魔角雙層石墨烯可以說是領頭羊！
 

 

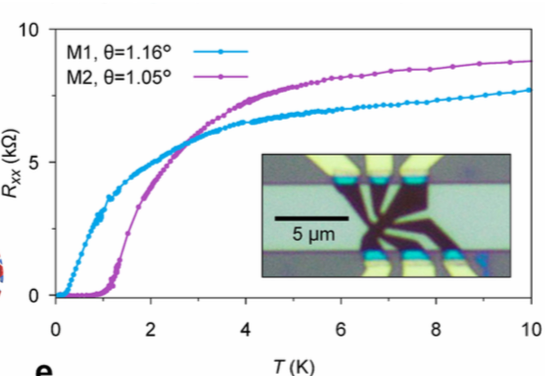
圖七_[3]

 

 

我們目前認識的超導：有一類是簡單金屬，能改變的實驗參數主要為溫度，且BCS理論架構可以完整解釋所有超導現象。另一類材料則是，一開始是絕緣體，必須經由摻雜，才能使得自由電子進入材料中，再經由降溫才形成超導，比如銅氧化物的高溫超導體就屬於這一類。目前並沒有一個單一理論可以完整的解釋所有這類超導所看見的實驗現象。這個魔角雙層石墨烯與高溫超導有許多相似之處：第一就是可以經由改變載子濃度變化造成強相關性質的絕緣體；第二是兩者的載子濃度都很低。

 

未來觀察重點

 

除了這兩篇自然雜誌論文的第一作者是同一位非常年輕且還在MIT就讀的物理博士學生外，這石墨烯中的強關聯物理已經引起研究社群的廣泛注意，arXiv的網站上也已經有一些超導或是強關聯理論的專家已提出一些理論模型。關於文獻2中報導的強關聯的絕緣態，第一個問題是為什麼只有在半填滿附近才顯現？這是否類似量子霍爾效應中，電子波函數的拓樸性質以及雜質等無序因素扮演關鍵角色？另外，電容值的量測很明顯看出當填入電子時，電容值因為形成強關聯態而改變，可是當填入電洞時，相對應的電容改變卻沒有發生？這樣的不對稱其實在固態系統中經常出現，是否有新的物理在其中？比起費米溫度，魔角雙層石墨烯可以被稱為高溫超導體，超導的波函數對稱性為何？當提高溫度進入金屬態時，是否也有奇異金屬的狀態發生？這許許多多的疑問，想必是未來固態物理社群想探索的新領域！

---

文獻參考

 

1. F. D. M. Haldane, Model for a quantum Hall effect without Landau levels: Condensed-matter realization of the "parity anomaly", Physical Review Letters 61, 2015, (31 Oct 1988)
2. Yuan Chao, et al., Correlated insulator behavior at half-filling in magic-angle graphene superlattice,  Nature 556, 80-84, (05 Apr 2018)
3. Yuan Chao, et al., Unconventional superconductivity in magic-angle graphene superlattice, Nature  556, 43-50, (05 Apr 2018)
4. Rafi Bistritzer and A. H. MacDonald, Moiré bands in twisted bilayer graphene, PNAS, vol. 108, no. 30, 12233-12237, (26 Jul 2011)
5. J. M. B. Lopes dos Santos, N. M. R. Peres, and A. H. Castro Neto, Graphene bilayer with a twist: Electronic structure, Physical Review Letters 99, 256802, (19 Dec 2007)

   ---

   繼續閱讀：石墨烯在化學氣相沉積法(CVD)製備上的挑戰與突破